Journal of Positioning, Navigation, and Timing (J Position Navig Timing; JPNT)
Indexed in KCI (Korea Citation Index)
OPEN ACCESS, PEER REVIEWED
pISSN 2288-8187
eISSN 2289-0866
Menu
Citation: Lee, J., Sun, A. K., Choi, H., & Lee, J., 2024, Regional Optimization of NeQuick G Model for Improved TEC Estimation, Journal of Positioning, Navigation, and Timing, 13, 63-73.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 March, Volume 13, Issue 1, pages 63-73. https://doi.org/10.11003/JPNT.2024.13.1.63
Received on 21 December 2023, Revised on 25 February 2024, Accepted on 07 March 2024, Published on 15 March 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/bync/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Jaeryoung Lee1, Andrew K. Sun1, Heonho Choi2, Jiyun Lee1†
1Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology, Daejeon 34141, Korea
2Korea Aerospace Research Institute, Daejeon 34133, Korea
†Corresponding Author: E-mail, dhhwang@cnu.ac.kr; Tel, +82-42-821-5670; Fax, +82-42-823-5436
NeQuick G is the ionosphere model utilized by Galileo single-frequency users to estimate the ionospheric delay on each user-satellite link. The model is characterized by the effective ionization level (Az) index, determined by a modified dip latitude (MODIP) and broadcast coefficients derived from daily global space weather observations. However, globally fitted Az coefficients may not accurately represent ionosphere within local area. This study introduces a method for regional ionospheric modeling that searches for locally optimized Az coefficients. This approach involves fitting TEC output from NeQuick G to TEC data collected from GNSS stations around Korea under various ionospheric conditions including different seasons and both low and high solar activity phases. The optimized Az coefficients enable calculation of the Az index at any position within a region of interest, accounting for the spatial variability of the Az index in a polynomial function of MODIP. The results reveal reduced TEC estimation errors, particularly during high solar activity, with a maximum reduction in the RMS error by 85.95%. This indicates that the proposed method for NeQuick G can effectively model various ionospheric conditions in local areas, offering potential applications in GNSS performance analyses for local areas by generating various ionospheric scenarios.
GNSS, ionospheric modeling, TEC, regional optimization, NeQuick
전리권은 태양 에너지로 인해 대기 분자들이 이온화되어 자유전자가 밀집된 대기의 고층 영역을 의미하며, 위성항법시스템 (Global Navigation Satellite System, GNSS) 신호의 주요한 오차 요소 중 하나로 작용한다. GNSS 신호가 전리권을 통과하면 해당 경로의 총전자량 (Total Electron Content, TEC)에 비례하는 지연 오차가 발생한다. 전리권에 분포한 전자 밀도는 시간, 위치, 계절, 및 태양 활동 등에 따라 변화하며, 이에 따라 GNSS 신호의 TEC 및 전리권 지연값 또한 변화하게 된다. 다양한 전리권 환경 하의 GNSS 신호의 전리권 지연값을 추정하기 위해, GNSS 사용자는 Klobuchar, NeQuick 등의 전리권 모델을 활용한다 (Klobuchar 1987, Hochegger et al. 2000).
Galileo에서 활용하는 전리권 예측 모델인 NeQuick G는 전리권 전자 밀도의 경험적 데이터를 활용하여 개발된 전리권 기상 모델 (Di Giovanni & Radicella 1990)을 기반으로 월별 전자 밀도의 분포를 예측하여 사용자에게 제공한다 (Hochegger et al. 2000, European Commission 2016). 해당 모델은 Az (Effective ionization level) 지수를 이용하여 태양 활동에 따른 전리권의 이온화 정도를 반영할 수 있기 때문에, 태양 주기에 따른 다양한 전리권 환경의 모델링이 가능하다. Az는 지자기위도 (Modified Dip Latitude, MODIP)에 따른 2차 다항식으로 표현되며, 그에 대한 계수인 Az 파라미터를 Galileo 위성에서 방송 정보로 사용자에게 제공한다 (European Commission 2016).
Galileo에서 방송하는 Az 파라미터는 전지구적으로 분포한 Galileo Sensor Station (GSS)에서 획득한 TEC를 기반으로 각 지역에 대한 Az 지수를 산출하고, MODIP에 따른 2차 다항식으로 전지구적인 Az 지수의 분포를 근사하여 사용자에게 Az 파라미터를 하루 주기로 제공한다 (Bidaine 2012). 하지만 이러한 방법으로 Az 파라미터를 산출할 경우, 높은 지자기 활동으로 인해 전리권의 전자 밀도 분포가 크게 변화할 때 국지적인 지역에 대한 전리권 모델링의 정확도가 저하될 수 있다 (Aragon-Angel et al. 2019).
사전 연구에서는 이러한 NeQuick G 모델의 한계점을 개선하기 위해, 특정 지역의 전자 밀도 관측치를 활용하여 NeQuick G 모델의 지역적인 전리층 모델링을 개선하는 연구가 수행된 바 있다 (Nava et al. 2005, Bidaine & Warnant 2011). Vuković & Kos (2017)는 중위도 지역의 전리권 모델링을 위해 특정 지역의 TEC 데이터를 기반으로 산출된 Az 지수의 지리적 적용 가능 범위를 분석하는 연구를 수행하였다. Osanyin et al. (2023)은 저위도 지역의 TEC 데이터 활용하여 특정 지역의 Az 지수를 산출하고 해당 지역에 대한 TEC 산출 모델을 개발하였다. 하지만 해당 연구에서는 지상국 주변의 특정 지역에 대한 Az 지수를 개별적으로 산출했으며, 이는 위치에 따른 Az 지수의 공간적 변화를 정확하게 반영하여 해당 지역 전체에 대한 전리권 모델링을 수행하는 데 한계가 있다.
본 논문에서는 국지적인 지역에 대한 전리권 모델링의 정확성 향상을 위해 NeQuick G 모델의 최적 Az 파라미터 산출 방법을 제안하였다. 한국 주변 지역의 지상국으로부터 획득한 TEC 데이터를 이용하여 NeQuick G 모델의 TEC 산출값과 TEC 관측치의 차이를 최소화하는 Az 파라미터를 도출하였으며, 이를 기반으로 한국 지역에 최적화된 NeQuick G 기반 전리권 모델링을 수행하였다. 해당 방법은 특정 지역 내에서 MODIP에 따른 Az의 연속적인 변화를 반영하며, 이를 기반으로 국지적인 지역에 대한 전리권 모델링을 수행한다.
본 논문은 다음과 같이 구성된다. 2장에서는 NeQuick G 모델의 TEC 산출 과정을 설명한다. 3장에서는 본 논문에서 활용한 GNSS 데이터 및 TEC 처리 과정을 기술하였다. 4장에서는 TEC 관측치에 대한 최적 Az 파라미터 산출 알고리즘을 제안하였다. 5장에서는 해당 알고리즘을 활용하여 한국 지역의 다양한 전리권 환경에 대해 산출된 최적 Az 파라미터의 모델링 결과를 보여주며, 6장에는 결론을 기술하였다.
NeQuick G 모델은 Galileo 단일 주파수 사용자의 전리권 지연값 보정을 위해 개발된 전리권 모델 생성 알고리즘으로, 경험적 데이터를 이용한 전자 밀도 모델을 기반으로 개발되었다 (Di Giovanni & Radicella 1990, Radicella & Zhang 1995). NeQuick G는 전리권을 구성하는 E층, F1층, F2층의 최대 전자 밀도 지점에 대한 임계 주파수(critical frequency)인 $f_{0,E}$, $f_{0, F1}$, $f_{0, F2}$ 그리고 투과 계수(transmission factor) $M$(3000) $F2$의 월별 카탈로그를 기반으로, 특정 지역 및 시간에 대한 전지구적인 3차원 전자 밀도 분포를 제공한다 (Hochegger et al. 2000, Radicella & Leitinger 2001). NeQuick G 모델에서 전자 밀도 계산에 이용되는 파라미터는 태양 활동을 정량화하는 Az 지수를 통해 결정되며, 해당 모델은 Az 지수 및 해당 방송 계수를 기반으로 다양한 태양 활동에 대한 전자 밀도 분포를 결정할 수 있다 (European Commission 2016).
Galileo의 단일 주파수 사용자를 위한 NeQuick G 알고리즘의 입력값은 사용자와 위성의 위치 및 시간과 Az 파라미터이며 각 입력값은 Table 1에 설명되어 있다 (European Commission 2016). 사용자-위성 경로에 대한 NeQuick G의 TEC 계산 과정은 다음과 같다 (European Commission 2016).
(i) 사용자 위치 ($\phi_1$, $\lambda_1$)를 기반으로 MODIP 산출
(ii) MODIP과 전달받은 Az 파라미터 ($a_0$, $a_1$, $a_2$)를 통해 사용자 위치에서의 Az 지수를 계산 (Eq. (1))
(iii) 위성 위치($\phi_2$, $\lambda_2$, $h_2$)와 사용자 위치($\phi_1$, $\lambda_1$, $h_1$) 사이의 경로를 여러 적분 지점으로 나눈 후, 각 적분 지점마다 NeQuick G 모델에 Az지수와 UT, month를 입력하여 전자 밀도 산출
(iv) 위성-사용자 경로를 따라 각 적분 지점의 전자 밀도를 적분하여 STEC 산출
Table 1. Input parameters of NeQuick G.
| Parameter | Description | Unit |
| $a_0$ $a_1$ $a_2$ $\phi_1$ $\lambda_1$ $h_1$ $\phi_2$ $\lambda_2$ $h_2$ UT month | Effective ionization level 1st order parameter Effective ionization level 2nd order parameter Effective ionization level 3rd order parameter Geodetic latitude from receiver Geodetic longitude from receiver Geodetic height from receiver Geodetic latitude from satellite Geodetic longitude from satellite Geodetic height from satellite UT time month | sfu sfu/deg sfu/deg2 deg deg meter deg deg meter hours dimensionless |
NeQuick G의 산출값인 STEC는 Eq. (2)를 통해 전리권 지연값 (m)로 변환될 수 있으며, (Hz)는 항법신호의 주파수를 의미한다 (European Commission 2016).
$$I=\dfrac{40.3}{f^2}STEC$$
기존 NeQuick G 모델은 위성과 수신기 위치를 모두 입력하여 STEC를 산출하지만, 본 연구에서는 Ionospheric Pierce Point (IPP)의 위치를 입력하여 Vertical TEC (VTEC)를 산출하도록 구현했다. Fig. 1은 NeQuick G 모델에 2023년 3월 21일에 방송된 Az 파라미터를 입력하여 산출한 전지구적 VTEC 분포의 예시를 나타낸다.
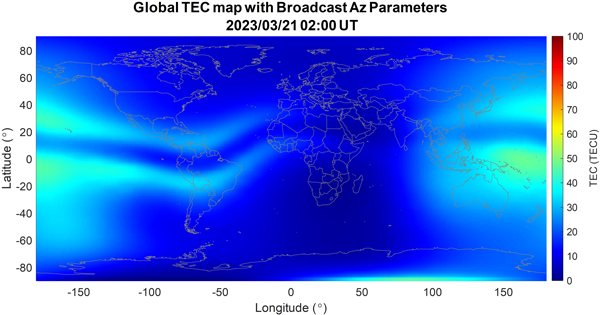
Fig. 1. Example of a global VTEC map generated using NeQuick G (March 21, 2023).
본 연구에서는 한국 및 그 주변 지역의 전리권 모델링을 위해 한국 내에 위치한 한국천문연구원 (KASI) 지상국 9곳과 한국 주변 지역 (위도: 20°~50°N, 경도: 110°~140°E)의 International GNSS Service (IGS) 지상국 15곳으로부터 GPS 데이터를 획득하였으며, 각 지상국의 위치 정보와 분포는 Table 2와 Fig. 2에 표시하였다.
Table 2. Specification of GNSS stations used in the study.
| Station ID | Latitude (°) | Longitude (°) | Network |
| AIRA BHAO BJFS BJNM CHAN CKSV DAEJ GAMG HKSL HKWS JEJU JFNG KMNM KOHG MKPO MLYN MTKA SBAO SHAO SKCH SKMA SMST SUWN TWTF USUD | 31.82 36.16 39.61 40.25 43.79 23.00 36.40 35.59 22.37 22.43 33.29 30.52 24.46 34.45 34.82 35.49 35.68 36.93 31.10 38.25 37.49 33.58 37.28 24.95 36.13 | 130.60 128.98 115.89 116.22 125.44 120.22 127.37 127.92 113.93 114.34 126.46 114.49 118.39 127.52 126.38 128.74 139.56 128.46 121.20 128.56 126.92 135.94 127.05 121.16 138.36 | IGS KASI IGS IGS IGS IGS IGS/KASI IGS IGS IGS KASI IGS IGS KASI KASI KASI IGS KASI IGS KASI KASI IGS IGS IGS IGS |
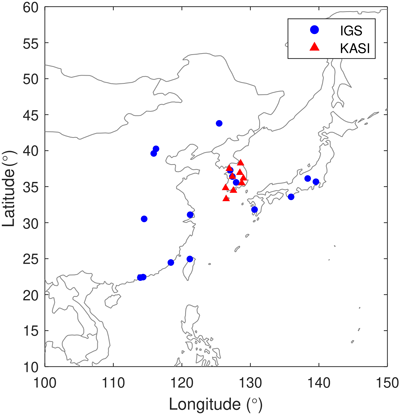
Fig. 2. Location of GNSS stations used in the study.
본 연구에서는 태양 활동에 따른 전리권 모델링의 성능을 평가하기 위해, 태양 극소기인 2019년과 태양 극대기인 2023년에 해당하는 TEC 관측치를 활용하여 모델링을 진행하였다. 또한 전리권의 계절적 변화를 고려하기 위해 태양 극소기와 극대기의 춘분, 하지, 추분 및 동지에 근접한 날짜를 선정하여 모델링에 활용하였다. Table 3은 각 날짜에 해당하는 지자기 지표를 나타내며 F10.7, Kp, 그리고 Dst는 각각 태양 활동의 정도와 지구 지자기 활동 정도, 그리고 지자기 폭풍 정도를 나타낸다 (Gonzalez et al. 1994, NASA Goddard Space Flight Center 2024). 본 연구에서 분석한 Table 3의 모든 날짜에서는 Kp 지수와 Dst의 절대값이 각각 4와 30 nT 이하로써 지자기 폭풍의 지자기 지수 임계값보다 낮으므로, 지자기 폭풍이 발생하지 않았으며 Kp 지수가 3 이하인 정상 상태에 해당한다 (Bartels 1963, Gonzalez et al. 1994, Miteva & Samwel 2023). 반면 태양 극소기의 2019년과 태양 극대기의 2023년의 F10.7 값에는 상당한 차이를 가지며, 해당 데이터를 활용하여 태양 활동에 따른 모델링 성능을 분석할 수 있다.
Table 3. Geomagnetic indices (NASA Goddard Space Flight Center 2024).
| Day | F10.7 (sfu) | Kp | Dst (nT) |
| 2019/03/21 2019/06/22 2019/09/23 2019/12/22 2023/03/21 2023/06/21 2023/09/23 2023/12/22 | 79.4 68.6 66.6 68.7 150.4 182.2 174.1 180.7 | 1.0 1.7 1.3 1.7 2.3 2.7 2.7 1.3 | -4 -2 -7 -16 3 -24 -26 -19 |
GNSS 데이터로부터 전리권 지연값 또는 TEC를 산출하는 알고리즘은 Fig. 3과 같다. 해당 알고리즘은 순서대로 원시 전리권 지연값 산출, 전처리, IFB 제거 그리고 VTEC 변환 과정을 통해 수행된다.
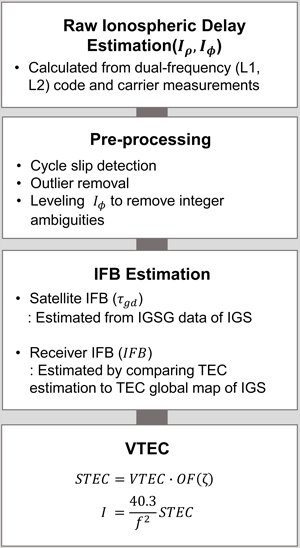
Fig. 3. Algorithm for generating TEC data.
3.2.1 원시 전리권 지연값 산출
GNSS 데이터에서 전리권 지연값은 L1 및 L2 이중주파수 측정치의 선형 조합으로 코드($\rho_{L1}$, $\rho_{L2}$) 및 반송파($\phi_{L1}$, $\phi_{L2}$) 측정치에 대해 각각 Eqs. (3), (4)와 같이 산출할 수 있다 (Jung & Lee 2012). $I_{\rho,L1}$및 $I_{\phi,L1}$는 $L1$코드 및 반송파 측정치를 통해 산출한 원시 전리권 지연값에 해당한다.
$$I_{\rho,L1}=\dfrac{\rho_{L2}-\rho_{L1}}{\gamma-1}=I_{L1}+\dfrac{c}{\gamma-1}(IFB+\tau_{gd})+\varepsilon_{\rho}$$
$$I_{\phi,L1}=\dfrac{\phi_{L2}-\phi_{L1}}{\gamma-1}=I_{L1}+\dfrac{c}{\gamma-1}(IFB+\tau_{gd})+\dfrac{N_{L1}-N_{L2}}{\gamma}+\varepsilon_{\phi}$$
$$\gamma=\dfrac{f_{L1}^{2}}{f_{L2}^{2}}$$
이때 $IFB$와 $\tau_{gd}$는 각각 수신기와 위성의 Inter-Frequency Bias (IFB)이며, $N_{L1}$과 $N_{L2}$는 반송파 측정치가 포함하는 모호정수이다. $\varepsilon_{\rho}$ 및 $\varepsilon_{\phi}$는 각각 코드와 반송파 측정치가 포함하는 다중경로 및 잡음 오차를 나타낸다. $f_{L1}$및 $f_{L2}$는 $L1$및 $L2$ 신호의 주파수이며, $c$는 진공에서의 빛의 속력에 해당한다.
3.2.2 전처리 과정
반송파 기반 전리권 지연값($I_{\phi}$)은 코드 기반 전리권 지연값($I_{\rho}$)에 비해 다중경로 및 잡음 오차의 크기가 작기 때문에 전리권 지연값 및 TEC 산출에 이용된다 (Jung & Lee 2012). 하지만 $I_{\phi}$는 모호정수를 포함하고 있기 때문에, 이를 보정하기 위해 사이클 슬립(cycle slip)과 아웃라이어(outlier)를 검출 및 제거하였다 (Jung & Lee 2012). 마지막으로 $I_{\rho}$를 기준으로 $I_{\phi}$의 레벨링(leveling)을 진행하여 반송파의 모호정수 $N_{L1}$, $N_{L2}$를 제거하였다 (Komjathy et al. 2007).
3.2.3 IFB 추정
전처리 과정을 통해 모호정수를 제거한 $I_{\phi}$예측치에는 위성 및 수신기의 IFB가 포함되어 있기 때문에, 정확한 전리권 지연값을 산출하기 위해서는 해당 바이어스 값을 제거하는 과정을 거친다. 위성 IFB ($\tau_{gd}$)는 IGS Ionosphere Associate Analysis Centers (IAACs)에서 제공하는 IONEX 정보를 통해 획득하여 제거할 수 있다 (Schaer et al. 1998, Hernández-Pajares et al. 2009). 반면 수신기 IFB의 경우, 해당 수신기의 GNSS 측정치를 기반으로 개별적으로 예측되어야 하며, 이를 위한 다양한 기법이 연구된 바 있다 (Ma & Maruyama 2003, Komjathy et al. 2007). 본 연구에서는 IAACs에서 처리하여 제공되는 IONEX 정보의 전지구적인 TEC 값을 활용하여 수신기 IFB 값을 예측하였다 (Arikan et al. 2008). 이 과정은 Eq. (6)과 같으며, 이때 STEC는 각 측정치의 시간 및 위치에 대해 IONEX 정보의 TEC 지도를 내삽하여 얻어진 VTEC 값을 기울기 계수를 통해 변환하여 산출된다. 각 수신기에 대해 일간 측정치를 모두 축적하여, Eq. (6)에서 목적 함수를 최소화하는 값을 수신기 IFB로 추정하였다.
$$IFB=\overset{argmin}{IFB}\left[\dfrac{f^2_{L1}}{40.3\cdot 10^{16}}\left(I_{\phi,L1}-\frac{c}{\gamma-1}(IFB+\tau_{gd})\right)-STEC\right]$$
3.2.4 VTEC 변환
$I_{\phi}$를 레벨링하고 위성 및 수신기의 IFB를 제거한 최종 결과값을 전리권 지연값(I) 근사치로 설정한다. 전리권 지연값은 Eq. (2)을 통해 STEC 값으로 변환될 수 있으며, 이는 Eq. (8)로 산출되는 기울기 계수 (Obliquity factor, OF)를 통해 Eq. (7)과 같이 VTEC로 계산된다 (Enge 1994). 이때 $\zeta$는 위성의 천정각(zenith angle)을 의미하며, RE는 지구의 평균 반지름, $h_I$는 전리권의 평균 고도인 350 km에 해당한다.
$$STEC=VTEC \cdot OF(\zeta)$$
$$OF(\zeta)=\left[1-\left(\dfrac{R_E \sin \zeta}{R_E+h_I}\right)^2\right]^{-\frac{1}{2}}$$
NeQuick G 모델은 특정 시간 및 위치에서의 Az 지수를 통해 전리권의 전자 밀도 분포를 산출한다. Eq. (1)에서와 같이 Az 지수는 MODIP에 대한 2차 다항식으로 표현되며, Az 파라미터 ($a_0$, $a_1$, $a_2$)를 통해 MODIP에 따른 Az 지수가 결정된다. Galileo의 기존 NeQuick G 모델은 전지구적으로 분포한 GSS 지상국에서 TEC 분포를 관측하며 각 지상국은 Az 지수를 개별적으로 산출한다. 각 GSS 지상국에서는 회귀분석을 통해 주변 지역의 TEC 관측치와 TEC 모델링 산출값의 root mean square (RMS) 차이가 최소가 되도록 하는 개별 Az 지수를 하루 주기로 계산한다. 그리고 모든 지상국의 Az 지수를 취합하고 해당 Az 지수 데이터를 MODIP에 대한 2차 다항식으로 근사하여 전지구적 전리권을 모델링하는 Az 파라미터를 산출한다 (Bidaine 2012).
기존 NeQuick G 모델의 Az 파라미터 산출 과정과는 달리, 본 연구에서는 관측 범위 내의 전체 TEC 관측치를 기반으로 회귀분석을 수행하여 Az 파라미터를 산출하였다. 해당 방법은 전체 TEC 관측치를 대상으로 모델링 오차가 최소가 되는 Az 파라미터를 산출한다. 이를 통해 각 위치에 해당하는 Az 지수와 TEC를 더욱 정확하게 산출하여 전체적인 모델링 오차를 줄일 수 있다.
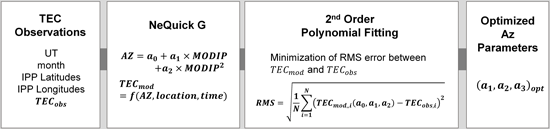
Fig. 4. Algorithm for optimizing Az coefficients.
본 연구에서 수행된 Az 파라미터의 최적화 과정은 Fig. 4와 같다. TEC 관측 데이터는 IPP의 위치 정보 및 시간 정보와 VTEC 값인 TECobs를 포함한다. 해당 IPP 위치 정보 및 시간 정보, 그리고 임의의 Az 파라미터를 NeQuick G 모델에 입력하여 TEC 모델링 산출값인 TECmod를 반환한다. 이후, TECmod와 TECobs의 차이가 최소가 되도록 하는 Az 파라미터를 찾기 위해 2차 다항 회귀분석을 수행한다. 이 과정에서 최소화해야 하는 목적 함수는 최소제곱법에 기반하여 N개의 TECmod와 TECobs의 RMS 오차로 정의되며, 해당 과정은 Eq. (9)로 표현된다. 본 연구에서는 해당 목적 함수의 최소값을 찾기 위해 Nelder-Mead Simplex 알고리즘을 사용하였다. 해당 알고리즘은 목적 함수의 구배를 연산할 필요가 없어 비선형 최적화 과정의 연산량을 줄일 수 있으며, 알고리즘의 초기 추정값이 최적해와 크게 근접하지 않아도 된다는 이점이 있다 (Lagarias et al. 1998). 초기 추정값으로는 해당 날짜의 Galileo Az 방송 파라미터를 입력하였으며, 이 방법을 통해 TEC 모델링 산출값의 RMS 오차가 최소가 되는 Az 파라미터를 최적 Az 파라미터 ($a_0$, $a_1$, $a_2$)opt
로 설정하여 그에 대한 TEC 모델링 결과인 TECopt를 산출하였다.
$$(a_0, a_1, a_2)_{opt}=\overset{argmin}{(a_0, a_1, a_2)}\sqrt{\dfrac{1}{N}\sum^{n}_{i=1}(TEC_{mod,i}(a_0, a_1, a_2)-(TEC_{obs,i})^2}$$
전리권 환경은 지역 시간에 따라 그 변화량과 분포가 다르기 때문에, 본 연구에서는 각 시간대 별 전리권 환경을 반영한 TEC 모델링을 위해 1시간 간격의 TEC 관측치에 대한 Az 파라미터를 산출하였다. 또한, 시간에 따른 TEC 변화 및 모델링 오차를 최소화하기 위해 각 시간대 별로 5분 간격의 TEC 데이터를 수집하여 최적 Az 파라미터 산출에 이용하였다.
본 연구에서는 한국 지역 TEC 관측치를 기반으로 최적 Az 파라미터를 도출하였으며, 해당 파라미터를 이용하여 모델링한 TECopt를 Galileo가 제공하는 기존의 Az 파라미터를 이용한 TECgal와 비교하여 성능을 분석하였다. 태양 활동의 정도를 반영하기 위해 태양 극소기의 2019년과 태양 극대기의 2023년의 데이터를 활용하였다. 연간 전리권의 계절적 변화를 반영하기 위해, 각 기간에서 춘분, 하지, 추분 및 동지에 근접한 날짜를 선정하여 시간별 TEC 모델링을 수행하였다. 최적 Az 파라미터의 모델링 성능을 평가하기 위해, 각 날짜에서 Galileo 위성이 송신한 Az 방송 파라미터에 대한 NeQuick G 모델의 TEC 산출값과 실제 TEC 관측치 간의 RMS 오차를 비교 대상으로 활용하였다.
Fig. 5는 태양 극소기인 2019년의 춘분, 하지, 추분 및 동지에 근접한 네 날짜의 2:00 UT (11:00 LT)에 대한 TEC 분포와 모델링 결과를 나타낸다. 왼쪽부터 차례대로 관측치인 TECops, Galileo Az 파라미터의 모델링 결과인 TECgal, 그리고 최적 Az 모델링 결과인 TECopt 분포를 나타낸다. Table 4는 각 날짜에 대해 최적화된 Az 파라미터 ($a_0$,$a_1$,$a_2$)opt와 방송 파라미터 ($a_0$,$a_1$,$a_2$)gal에 대한 NeQuick G 모델의 TEC 산출값과 실제 관측치인 TECobs의 RMS 오차를 보여준다. 방송 Az 파라미터을 이용할 경우, 모든 날짜에 대해 RMS 오차는 4.13~11.73 TECU의 값을 가지며, 최적 Az 파라미터를 이용할 경우, RMS 오차는 1.09~6.24 TECU으로 더 적은 값을 가진다. 이 결과는 Az 파라미터의 최적화가 해당 지역에 대한 전리권 모델링의 정확성을 향상시켰음을 보여준다.
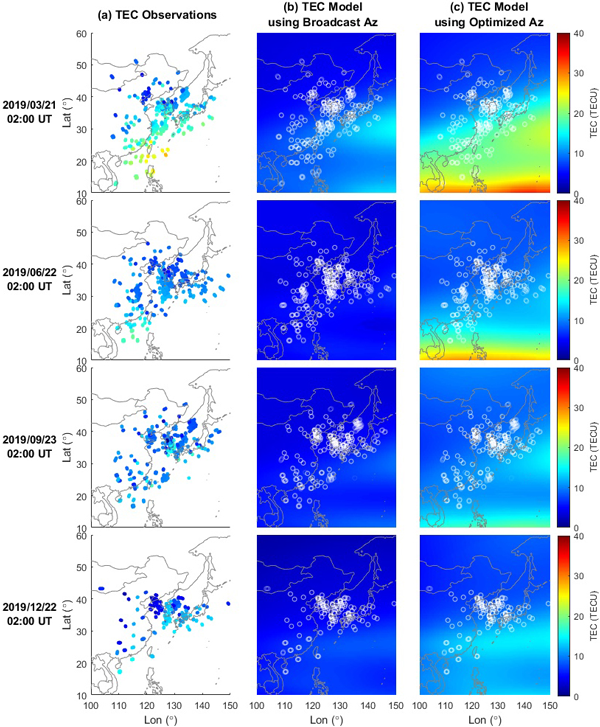
Fig. 5. Results of ionospheric modeling on the low solar activity days (2019). (a) Observed TEC. (b) TEC map modeled with broadcast Az parameters. (c) TEC map modeled with optimized Az parameters.
Table 4. Modeling results on low solar activity days (2019).
| Day | Broadcast Az parameters | Optimized Az parameters | ||
| ($a_0$,$a_1$,$a_2$)gal | RMS error (TECU) | ($a_0$,$a_1$,$a_2$)opt | RMS error (TECU) | |
| 2019/03/21 2019/06/22 2019/09/23 2019/12/22 | (39.75, 0.14, 0.0030) (23.75, -0.0024, 0.011) (28.00, 0.0024, 0.011) (29.25, 0.39, 0.000061) | 7.26 5.97 5.55 5.80 | (106.83, -1.66, 0.022) (97.00, -1.99, 0.040) (60.05, -0.74, 0.035) (60.06, -0.0099, 0.019) | 2.87 1.80 2.62 3.26 |
Fig. 6은 태양 극대기인 2023년의 각 시기 별 2:00 UT (11:00 LT)에 대한 TEC 관측치인 TECobs, Galileo Az 파라미터의 모델링 결과인 TECgal, 그리고 최적 Az 모델링 결과인 TECobt 분포를 나타낸다. Table 5는 Galileo 방송 Az 파라미터 및 최적 Az 파라미터에 대한 RMS 오차를 나타낸다. 방송 Az 파라미터를 이용할 경우, 3.66~28.83 TECU의 RMS 오차를 가지는 반면, 최적 Az 파라미터를 이용할 경우, RMS 오차는 1.89~11.64 TECU로 더 작은 값을 가진다. 해당 결과는 태양 활동이 활발하여 국지적 전리권 편차가 커지는 경우, 최적 Az 파라미터 산출을 통해 전리권 모델링의 정확도를 향상시킬 수 있음을 나타낸다.
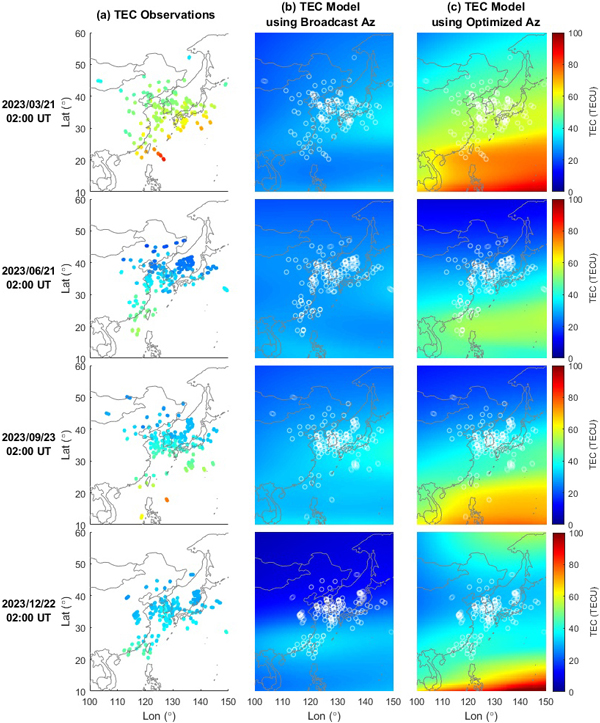
Fig. 6. Results of ionospheric modeling on the high solar activity days (2023). (a) Observed TEC. (b) TEC map modeled with broadcast Az parameters. (c) TEC map modeled with optimized Az parameters.
Table 5. Modeling results on high solar activity days (2023).
| Day | Broadcast Az parameters | Optimized Az parameters | ||
| ($a_0$,$a_1$,$a_2$)gal | RMS error (TECU) | ($a_0$,$a_1$,$a_2$)opt | RMS error (TECU) | |
| 2023/03/21 2023/06/21 2023/09/23 2023/12/22 | (129.25, -0.25, 0.021) (162.00, 0.59, 0.014) (158.25, 0.15, 0.010) (154.25, -0.72, -0.000031) | 25.63 10.04 7.49 13.31 | (269.54, -2.02, 0.023) (245.55, 1.58, -0.067) (239.60, -1.64, 0.0053) (231.38, -5.92, 0.13) | 3.67 3.45 3.60 2.51 |
시간에 따른 모델링 결과를 분석하기 위해, 한 시간 간격으로 모델링을 진행하고 오차를 비교하였다. 각 시간마다 한국 주변의 지상국 총 24곳에서 5분 동안 관측한 IPP에서의 TEC 데이터를 수집하였으며, 해당 데이터로부터 최적 Az 파라미터를 산출하였다. Figs. 7과 8은 각각 태양 극소기(2019년)와 태양 극대기(2023년)의 각 날짜별 모델링 오차를 나타낸다. 해당 그래프는 Galileo Az 방송 파라미터와 최적 Az 파라미터를 사용한 NeQuick G 모델의 TEC 산출값과 TEC 관측치의 RMS 오차를 나타낸다.
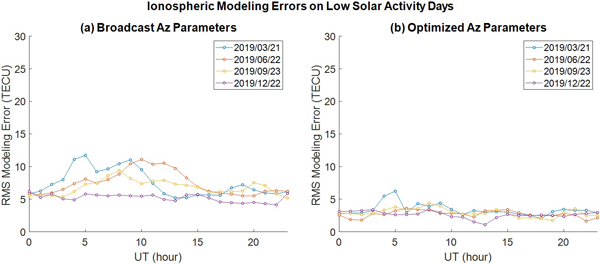
Fig. 7. Comparison of TEC modeling RMS errors on the low solar activity days (2019). (a) RMS modeling errors using broadcast Az parameters. (b) RMS modeling errors using optimized Az parameters.
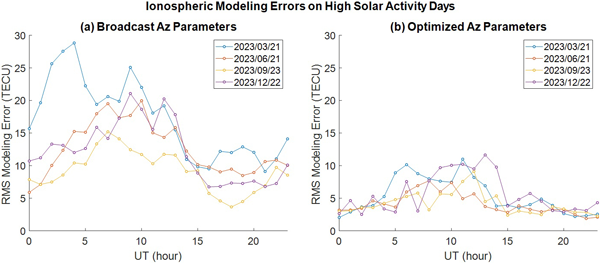
Fig. 8. Comparison of TEC modeling RMS errors on the high solar activity days (2023). (a) RMS modeling errors using broadcast Az parameters. (b) RMS modeling errors using optimized Az parameters.
태양 극소기의 Galileo Az 방송 파라미터에 대한 NeQuick G 모델의 TEC 산출값은 TEC 관측치와 비교하여 평균 6.74 TECU의 모델링 RMS 오차를 보인다. 반면, 최적 Az 파라미터에 대한 NeQuick G 모델은 더 작은 평균 2.92 TECU의 RMS 오차를 보인다. 태양 극대기에서는 두 모델의 성능 차이가 더욱 뚜렷해지며, Fig. 8에서 확인할 수 있다. Galileo Az 방송 파라미터에 대한 NeQuick G 모델의 TEC 산출값은 평균 12.81 TECU의 RMS 오차를 갖는 반면, 최적 Az 파라미터에 대한 NeQuick G 모델의 오차는 평균 4.84 TECU 로 감소하였다. 해당 결과는 기존의 방송 Az 파라미터에 비해, 최적 Az 파라미터의 NeQuick 모델이 활발한 태양 활동 하에서 TEC 산출의 정확성을 향상시킬 수 있음을 보여준다.
해당 결과를 통해, 한국 지역 TEC 데이터를 활용한 최적 Az 파라미터는 Galileo 위성에서 방송된 Az 파라미터보다 한국 지역의 국지적인 전리권을 보다 정확하게 모델링함을 확인할 수 있다. Galileo의 Az 방송 파라미터는 전지구적 전리권 관측치를 기반으로 산출한 값으로 더욱 광범위한 영역의 전리권 경향을 나타낼 수 있지만, 한국 지역의 국지적인 전리권을 모델링하는 경우 실제 TEC 관측치와의 상당한 값의 오차가 발생했다. 반면 본 연구에서 제안한 최적 Az 파라미터 산출 알고리즘은 한국 지역의 전리권을 기준으로 Az 파라미터를 산출했기 때문에, 한국 지역의 국지적인 전리권 환경을 더욱 정확히 반영할 수 있다. 해당 결과를 통해, 본 연구에서 제안한 최적 Az 파라미터 산출 알고리즘은 국지적인 지역의 전리권을 더욱 정확하게 모델링할 수 있다는 점을 확인할 수 있다.
전지구적 전리권을 대상으로 산출한 기존의 Galileo 방송 Az 파라미터는 국지적인 지역의 전리권을 모델링하는 경우 TEC 산출값에 상당한 오차가 발생할 수 있다. 이러한 점을 개선하기 위해 본 연구에서는 국지적 지역의 전자 밀도 분포 모델링에 적합한 최적 Az 파라미터 산출 방법을 제안하였다. 한국 지역의 TEC 관측치를 기반으로 최적 Az 파라미터를 산출하는 방법을 통해 NeQuick G 모델의 TEC 산출값과 실제 측정치 간의 RMS 오차를 최소화하는 최적 Az 파라미터 ($a_0$, $a_1$, $a_2$)를 산출하였다.
해당 방법을 태양 극소기인 2019년에 적용한 결과, 최적 Az 파라미터에 대한 NeQuick 모델의 RMS 오차는 평균 2.92 TECU로, Galileo의 Az 파라미터에 대한 모델의 RMS 오차인 평균 6.74 TECU에 비해 감소하였다. 태양 극대기인 2023년 또한 최적 Az 파라미터에 대한 모델의 RMS 오차는 평균 4.84 TECU이며, Galileo의 Az 파라미터에 대한 모델의 RMS 오차인 평균 12.81 TECU에 비해 상당히 감소하였다. 해당 결과는 최적 Az 파라미터를 산출함으로써 태양 활동이 적은 경우뿐만 아니라 태양 활동이 활발하여 전리권의 시/공간적 변화가 심한 경우도 지역적 전리권의 편차를 보다 정확하게 모델링할 수 있음을 보여준다.
따라서, 지역적 TEC 데이터를 기반으로 한 최적 Az 파라미터 산출 알고리즘은 국지적인 전리권의 다양한 상황을 효과적으로 모델링할 수 있다. 해당 기법은 GNSS 성능 평가 및 다양한 지역적 전리권 시나리오 생성에 활용될 수 있으며, 이를 활용하여 지역적 전리권의 모델링 정확도를 향상시킬 수 있다.
Aragon-Angel, A., Zürn, M., & Rovira-Garcia, A. 2019, Galileo ionospheric correction algorithm: An optimization study of NeQuick-G, Radio Science, 54, 1156-1169. https://doi.org/10.1029/2019RS006875
Arbesser-Rastburg, B. 2006, The Galileo single frequency ionospheric correction algorithm, Third European Space Weather Week, Brussels, Belgium, Nov 13-17, 2006. https://sidc.be/esww3/presentations/Session4/Arbesser.pdf
Arikan, F. E. Z. A., Nayir, H., Sezen, U. M. U. T. & Arikan, O. 2008, Estimation of single station interfrequency receiver bias using GPS-TEC, Radio Science, 43, 1-13. https://doi.org/10.1029/2007RS003785
Bartels, J. 1963, Discussion of time-variations of geomagnetic activity, indices Kp and Ap, 1932-1961, Annales de Geophysique, 19, 1.
Bidaine, B. 2012, Ionosphere modelling for Galileo single frequency users, Doctoral thesis, ULiège – Université de Liège. https://hdl.handle.net/2268/131216
Bidaine, B., Lonchay, M., & Warnant, R. 2013, Galileo single frequency ionospheric correction: performances in terms of position, GPS Solutions, 17, 63-73. https://doi.org/10.1007/s10291-012-0261-0
Bidaine, B. & Warnant, R. 2011, Ionosphere modelling for Galileo single frequency users: illustration of the combination of the NeQuick model and GNSS data ingestion, Advances in Space Research, 47, 312-322. https://doi.org/10.1016/j.asr.2010.09.001
Di Giovanni, G. & Radicella, S. M. 1990, An analytical model of the electron density profile in the ionosphere, Advances in Space Research, 10, 27-30. https://doi.org/10.1016/0273-1177(90)90301-F
Enge, P. K. 1994, The global positioning system: Signals, measurements, and performance, International Journal of Wireless Information Networks, 1, 83-105. https://doi.org/10.1007/BF02106512
European Commission 2016, European GNSS (Galileo), Open Service-Ionospheric Correction Algorithm for Galileo Single Frequency Users, Issue 1.2, available from: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_Ionospheric_Model.pdf
Gonzalez, W. D., Joselyn, J. A., Kamide, Y., Kroehl, H. W., Rostoker, G., et al. 1994, What is a geomagnetic storm?, Journal of Geophysical Research: Space Physics, 99, 5771-5792. https://doi.org/10.1029/93JA02867
Hernández-Pajares, M., Juan, J. M., Sanz, J., Orus, R., Garcia-Rigo, A., et al. 2009, The IGS VTEC maps: a reliable source of ionospheric information since 1998, Journal of Geodesy, 83, 263-275. https://doi.org/10.1007/s00190-008-0266-1
Hochegger, G., Nava, B., Radicella, S., & Leitinger, R. 2000, A family of ionospheric models for different uses, Physics and Chemistry of the Earth, Part C: Solar, Terrestrial & Planetary Science, 25, 307-310. https://doi.org/10.1016/S1464-1917(00)00022-2
Jung, S. & Lee, J. 2012, Long-term ionospheric anomaly monitoring for ground based augmentation systems, Radio Science, 47, 1-12. https://doi.org/10.1029/2012RS005016
Klobuchar, J. A. 1987, Ionospheric time-delay algorithm for single-frequency GPS users, IEEE Transactions on aerospace and electronic systems, AES-23, 325-331. https://doi.org/10.1109/TAES.1987.310829
Komjathy, A., Sparks, L., & Mannucci, A. J. 2007, Generating high precision ionospheric ground-truth measurements, U.S. Patent No. 7,289,061, Oct 30, 2007.
Lagarias, J. C., Reeds, J. A., Wright, M. H., & Wright, P. E. 1998, Convergence properties of the Nelder–Mead simplex method in low dimensions, SIAM Journal on Optimization, 9, 112-147. https://doi.org/10.1137/S1052623496303470
Ma, G. & Maruyama, T. 2003, Derivation of TEC and estimation of instrumental biases from GEONET in Japan, Annales Geophysicae, 21, 2083-2093. https://doi.org/10.5194/angeo-21-2083-2003
Miteva, R. & Samwel, S. W. 2023, Catalog of Geomagnetic Storms with Dst Index≤−50 nT and Their Solar and Interplanetary Origin (1996–2019), Atmosphere, 14, 1744. https://doi.org/10.3390/atmos14121744
NASA Goddard Space Flight Center, GSFC/SPDF OMNIWeb Data Explorer [Internet], cited 2024 Feb 19, available from: https://omniweb.gsfc.nasa.gov/form/dx1.html
Nava, B., Coïsson, P., Miró Amarante, G., Azpilicueta, F. J., & Radicella, S. M. 2005, A model assisted ionospheric electron density reconstruction method based on vertical TEC data ingestion, Annals of Geophysics, 48, 313-320. https://doi.org/10.4401/ag-3203
Osanyin, T. O., Candido, C. M. N., Becker-Guedes, F., Migoya-Orue, Y., Habarulema, J. B., et al. 2023, Performance of a locally adapted NeQuick-2 model during high solar activity over the Brazilian equatorial and low-latitude region, Advances in Space Research, 72, 5520-5538. https://doi.org/10.1016/j.asr.2023.07.018
Radicella, S. M. & Leitinger, R. 2001, The evolution of the DGR approach to model electron density profiles, Advances in Space Research, 27, 35-40. https://doi.org/10.1016/S0273-1177(00)00138-1
Radicella, S. M. & Zhang, M. L. 1995, The improved DGR analytical model of electron density height profile and total electron content in the ionosphere, Annali di Geofisica, 38, 35-41. https://doi.org/10.4401/ag-4130
Rawer, K. A. R. L. 1963, Propagation of decameter waves (HF band), Meteorological and Astronomical Influences on Radio Wave Propogation (Oxford: Pergamon Press), p.221.
Schaer, S., Gurtner, W., & Feltens, J. 1998, IONEX: The ionosphere map exchange format version 1.1, In Proceedings of the IGS AC workshop, Darmstadt, Germany, Feb 9-11 1998. http://ftp.aiub.unibe.ch/ionex/draft/ionex11.pdf
Vuković, J. & Kos, T. 2017, Locally adapted NeQuick 2 model performance in European middle latitude ionosphere under different solar, geomagnetic and seasonal conditions, Advances in Space Research, 60, 1739-1750. https://doi.org/10.1016/j.asr.2017.05.007
The KASINET data are available at ftp://gnss-ftp.kasi.re.kr. The IGS data are available at https://cddis.nasa.gov/archive/gnss/data. The NeQuick model is available at https://www.mathworks.com/matlabcentral/fileexchange/109159-nequick-g.
Conceptualization, Jaeryoung Lee and Andrew K. Sun; methodology, Jaeryoung Lee; analysis & investigation, Jaeryoung Lee, Jiyun Lee, and Heonho Choi; data processing, Andrew K. Sun and Jaeryoung Lee; writing—original draft preparation, Jaeryoung Lee; writing—review and editing, Andrew K. Sun, Jiyun Lee, and Heonho Choi; supervision, Jiyun Lee; project administration, Heonho Choi.
The authors declare no conflict of interest.