Journal of Positioning, Navigation, and Timing (J Position Navig Timing; JPNT)
Indexed in KCI (Korea Citation Index)
OPEN ACCESS, PEER REVIEWED
pISSN 2288-8187
eISSN 2289-0866
Menu
Citation: Kim, G. M., Kim, G., & Park, C.., 2024, Developing GPS Code Multipath Grid Map (CMGM) of Domestic Reference Station, Journal of Positioning, Navigation, and Timing, 13, 85-92.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 March, Volume 13, Issue 1, pages 85-92. https://doi.org/10.11003/JPNT.2024.13.1.85
Received on 31 January 2024, Revised on 15 February 2024, Accepted on 22 February 2024, Published on 15 March 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/bync/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Gyu Min Kim1, Gimin Kim2, Chandeok Park1†
1Department of Astronomy, Yonsei University, Seoul 03722, Korea
2Space Geodesy Group, Korea Astronomy and Space Science Institute, Daejeon 34055, Korea
†Corresponding Author: E-mail, dhhwang@cnu.ac.kr Tel: +82-42-821-5670 Fax: +82-42-823-5436
This study develops a Global Positioning System (GPS) Code Multipath Grid Map (CMGM) of each individual domestic reference station from the extracted code multipath of measurement data. Multipath corresponds to signal reflection/refraction caused by obstacles around the receiver antenna, and it is a major source of error that cannot be eliminated by differencing. From the receiver-independent exchange format (RINEX) data for two days, the associated code multipath of a satellite tracking arc is extracted. These code multipath data go through bias correction and interpolation to yield the CMGM with respect to the azimuth and elevation angles. The effect of the CMGM on multipath mitigation is then quantitatively analyzed to improve the Root Mean Square (RMS) of averaged pseudo multipath. Furthermore, the single point positioning (SPP) accuracy is analyzed in terms of the RMS of the horizontal and vertical errors. During two weeks in February 2023, the RMSs of the averaged pseudo multipath for five reference stations decreased by about 40% on average after CMGM application. Also, the SPP accuracies increased by about 7% for horizontal errors and about 10% for vertical errors on average after CMGM application. The overall quantitative analysis indicates that the proposed approach will reduce the convergence time of Differential Global Navigation Satellite System (DGNSS), Real-Time Kinematic (RTK), and Precise Point Positioning (PPP)-RTK correction information in real-time to use measurement data whose code multipath is corrected and mitigated by the CMGM.
CMGM, code multipath mitigation, GPS, reference station, SPP
제4차 산업혁명 시대가 도래함에 따라 자율주행, 항공 및 선박 서비스, 첨단 농업 등 다양한 분야에서 위성 항법 시스템을 통한 고정밀 측위 서비스의 필요성이 증가하고 있다. 고정밀 측위를 수행하기 위해서는 위성 항법 시스템에 존재하는 전리층 오차, 대류층 오차, 위성 궤도 및 시계 오차, 다중경로오차 등 다양한 오차요인에 대한 보정이 필수적이기 때문에 Differential Global Navigation Satellite System (DGNSS), Real Time Kinematic (RTK), Network-RTK, Precise Point Positioning (PPP)-RTK와 같은 Global Navigation Satellite System (GNSS) 보강시스템이 활용되고 있다. GNSS 보강시스템은 보정치를 추정하는 과정에서 차분기법을 활용하는 것이 특징인데, 상기 오차요인 중에서 다중경로오차는 차분기법을 통해 제거되지 않기 때문에 GNSS 보강시스템 분야에서 중요한 오차요인이다 (Dong et al. 2016).
다중경로오차를 보정해줌으로써 GNSS 보강시스템의 성능을 향상시킬 수 있다 (Lu et al. 2021). 다중경로오차 보정 기법은 하드웨어 관련 기법과 자료처리 관련 기법으로 구분할 수 있으며, 자료처리 관련 기법 중 하나로서 고정 수신기 위로 인공위성이 공간상에서 반복적으로 뜨고 지는 성질을 활용한 다중경로오차 격자지도 기법이 있다. 격자지도를 활용한 다중경로오차 보정 기법은 모든 위성 항법 시스템에 적용이 가능하고 위성의 기동에 따른 영향을 덜 받으며 실시간과 후처리 방식 모두 활용 가능하다는 장점을 가진다 (Fuhrmann et al. 2015).
Fuhrmann et al. (2015), Dong et al. (2016), Wang et al. (2020)에서는 PPP 잔차 (Residual)를 활용하여 생성한 격자 데이터로 반송파 위상 다중경로오차 격자지도를 만들고 지도 적용 전후의 잔차를 비교함으로써 성능 분석을 수행하였다. 세 연구의 산출물인 반송파 위상 다중경로오차 격자지도는 코드 다중경로오차 보정이 불가능하다는 한계점이 존재한다.
코드 다중경로오차 보정은 코드 관측데이터 기반 GNSS 보강시스템인 DGNSS의 성능향상 뿐만 아니라 반송파 위상 관측데이터 기반 GNSS 보강시스템인 PPP-RTK에서도 초기 수렴 시간을 단축시켜 성능향상을 기대할 수 있으므로 GNSS 보강시스템에 유용한 기술이다. Kee & Parkinson (1994)에서는 Code Minus Carrier (CMC) 기법을 통해 코드 다중경로오차를 추출하고, Pseudo Random Noise (PRN)에 따른 상대 바이어스를 제거하여 코드 다중경로오차 격자지도를 만들고, 지도 적용 전후 잔차를 통한 성능 분석을 수행하였다. Lu et al. (2021)에서는 PPP 잔차로부터 코드 의사거리 잔차와 반송파 위상 잔차를 추출한 후, 파라미터 추정 결과를 통해 코드 및 반송파 위상 다중경로오차 격자지도를 만들고, 지도 적용 전후 PPP 잔차, 측위 정밀도, 수렴 시간을 통한 성능 분석을 수행하였다. 상술한 연구들에서 기준국 수신기에 대한 분석은 수행되지 않았으며 다중경로오차와 수신기 잡음을 분리하는 Smoothing 기법과 격자지도에 값을 분배하는 Gridding 기법이 한가지로만 수행되었다. 또한 성능 분석 기간이 1주일 이내로 다소 짧게 설정되었으며 코드 다중경로오차 보정 효과가 가장 직접적으로 나타나는 Single Point Positioning (SPP) 정확도 변화에 대한 분석을 확인할 수 없었다.
본 연구에서는 국내 기준국 수신기의 1초간격 Global Positioning System (GPS) 관측데이터로부터 CMC 기법을 통해 코드 다중경로오차를 추출하고 3종류의 Smoothing 기법과 3종류의 Gridding 기법을 사용하여 코드 다중경로오차 격자지도 Code Multipath Grid Map (CMGM)을 생성한 후, 코드 다중경로오차 보정 정도 및 SPP 정확도 향상에 대한 CMGM의 성능 분석을 2주의 기간동안 수행한다.
본 논문의 2장에서는 CMGM 생성과정과 적용 방식을 제시하고, 3장에서는 코드 다중경로오차 보정 정도 및 SPP 정확도 향상에 대한 성능 분석 결과를 제시한 뒤, 4장에서 결론을 제시한다.
본 연구에서는 2023년 2월 7~20일 충주(CCHJ), 어청도(EOCH), 안흥(ANHN), 소청도(SOCH), 말도(MLDO) 기준국에서 수신하는 1초 간격 Receiver Independent Exchange Format (RINEX) 데이터를 확보한 뒤, 이틀 단위로 데이터를 합쳐 하나의 블록을 구성한다. CMC 기법은 사이클슬립이 발생하지 않는 온전한 아크(Arc)만 사용할 수 있기 때문에 블록 데이터에서 GPS PRN별로 가장 긴 아크만을 남긴 후 고도각 제한을 10˚로 적용하여 최종 블록을 완성한다. 사이클슬립은 Eq. (1)과 같이 Geometry-Free 조합을 사용하여 탐지한다.
$$\Phi_G=\Phi_1 – \Phi_2, \quad R_G=R_2 – R_1$$
여기서 첨자 1, 2는 각각 L1 (1575.42 MHz), L2 (1227.60 MHz) 주파수를 의미하고 $\phi$는 반송파 위상 의사거리, R은 코드 의사거리를 의미한다. Fig. 1은 2023년 2월 12~13일 충주 기준국의 GPS 관측데이터를 통해 생성한 블록에서 나타나는 위성들의 고도각을 나타낸다.
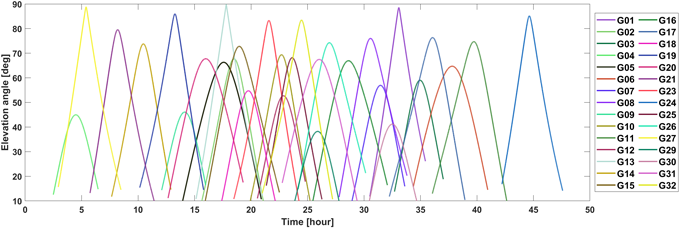
Fig. 1. Elevation angle for block data of GPS at CCHJ station.
본 연구에서는 CMC 기법을 사용하여 관측데이터로부터 코드 다중경로오차를 추출한다 (Yedukondalu et al. 2011, García & Woodhouse 2020, Caamano et al. 2020). CMC 기법은 Eq. (2)와 같이 코드의사거리 데이터와 반송파 위상 의사거리 데이터의 차이를 계산하는 것이 핵심이다. $I$는 전리층 지연오차, $M$은 코드 다중경로오차, $B$는 모호정수 관련 항, $\lambda_1 w$는 위상 말림 효과(Phase wind-up), $m$은 반송파 위상 다중경로오차, $\varepsilon$은 수신기 잡음, $f$는 주파수를 의미한다. Eq. (3)과 같이 이중 주파수를 사용하여 전리층 지연오차 항을 소거시킨 후 Eq. (4)에서 Pseudo Multipath (MP) 값을 얻을 수 있다.
$CMC_1 \equiv R_1 – \Phi_1 = 2I_1 + M_1 – B_1 – \lambda_1 w – m_1 – \varepsilon_1$
$$CMC_2 \equiv R_2 – \Phi_2 = 2I_2 + M_2 – B_2 – \lambda_2 w – m_2 – \varepsilon_2$$
$$I_1=\dfrac{f^2_2}{f^2_1 – f^2_2}(\Phi_1-\Phi_2), \quad I_2=\dfrac{f^2_1}{f^2_2 – f^2_1}(\Phi_2-\Phi_1)$$
$MP_1 \equiv CMC_1 – 2I_1 = R_1 – \dfrac{f^2_1 + f^2_2}{f^2_1 – f^2_2}\Phi_1 + \dfrac{2f^2_2}{f^2_1 – f^2_2}\Phi_2=M_1-B_1-\varepsilon_1$
$$MP_2 \equiv CMC_2 – 2I_2 = R_2 – \dfrac{2f^2_1}{f^2_1 – f^2_2}\Phi_1 + \dfrac{f^2_1 + f^2_2}{f^2_1 – f^2_2}\Phi_2=M_2-B_2-\varepsilon_2$$
반송파 위상 다중경로오차와 위상 말림 효과의 크기는 다른 항들에 비해 매우 작기 때문에 무시할 수 있으며 사이클슬립이 발생하지 않는 아크를 사용하였기 때문에 모호정수 관련 항($B$)은 변하지 않는 상수로 가정할 수 있다. 따라서 $MP_1$, $MP_2$의 평균 바이어스를 제거해줌으로써 모호정수 관련 항(B)을 소거할 수 있으며 Smoothing 기법을 사용하여 수신기 잡음($\varepsilon$)의 영향을 감소시킴으로써 Eq. (5)와 같이 최종적으로 Averaged Pseudo Multipath (AMP)를 얻을 수 있다.
$$MP_{i,biascorrection}=MP_i-\bar{MP_i}, \quad AMP_i \equiv \widehat{MP}_{i,biascorrection} \quad (i=1, 2) $$
Smoothing 기법으로는 이동창 (Moving window) 기법을 사용하며, 대표값으로는 각각 평균, 중앙값, 가우시안가중평균을 사용하여 3종류의 Smoothing을 수행한다. 창의 크기는 Translate Edit Quality Check (TEQC) 설정을 참고하여 50으로 설정한다 (Estey & Wier 2014). Fig. 2는 2023년 2월 12~13일 충주 기준국의 블록 데이터에서 GPS PRN01의 L1, L2 주파수에 대한 $AMP_1$, $AMP_2$를 고도각에 대하여 나타낸 그래프이다. 고도각이 20˚ 이하인 구간에서 $AMP_1$의 표준편차는 0.36 m, 80˚ 이상인 구간에서 0.09 m로 고도각이 높아질수록 다중경로오차가 줄어드는 경향성을 확인할 수 있다.
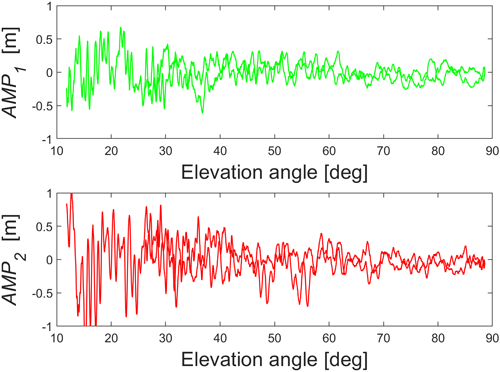
Fig. 2. Elevation dependency of AMP (GPS PRN01).
마지막 과정으로 고정 수신기에 대하여 동일한 방위각과 고도각 방향으로부터 입사한 신호의 다중경로오차는 동일한 성질을 활용하여 GPS PRN별 상대 바이어스를 보정한다 (Kee & Parkinson 1994). Fig. 3은 2023년 2월 12~13일 충주 기준국의 블록데이터를 사용하여 기준위성인 GPS PRN20에 대하여 GPS PRN01의 상대 바이어스를 보정하는 그래프 Fig. 3a와 상대 바이어스 보정을 마친 모든 GPS PRN의 $AMP_1$을 방위각과 고도각에 따라 나타낸 그래프 Fig. 3b이다.
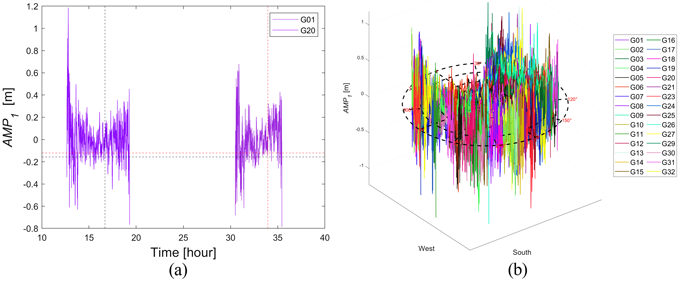
Fig. 3. Relative bias correction (a) and final plot of AMP1 about all GPS PRNs (b).
CMGM은 $AMP$ 데이터로부터 계산된 값이 저장되는 격자지도이다. 격자점 주변으로 분포하고 있는 다수의 데이터를 대표하는 값을 격자점에 저장하는 과정을 Gridding이라 하며 (Bilich & Larson 2007), 본 연구에서는 Nearest Neighbor, Nearby Group, Inverse Distance Weighting (IDW) 기법을 사용하여 3 종류의 Gridding을 수행한다. Nearest Neighbor 기법은 격자점으로부터 거리가 가장 가까운 10개의 데이터를 뽑고 해당 데이터들의 평균을 산출하여 격자점에 저장한다. Nearby Group 기법은 격자점으로부터 방위각과 고도각의 차이가 특정 범위 이내에 있는 데이터 그룹을 만들고 해당 그룹의 중앙값을 산출하여 격자점에 저장한다. IDW 기법은 격자점으로부터의 거리에 반비례하는 가중치 함수를 격자점으로부터 거리가 가장 가까운 10개의 데이터에 적용하여 계산한 값을 격자점에 저장한다. Fig. 4는 2023년 2월 12~13일 충주 기준국의 블록데이터에 대해 Nearby Group 기법을 사용하여 얻은 CMGM을 나타낸다. 고도각이 20˚ 이하인 구간에서 CMGM 격자점 데이터의 표준편차는 0.32 m, 80˚ 이상인 구간에서 0.09 m로 낮은 고도각 영역에서 다중경로오차가 크게 나타나는 경향성을 확인할 수 있다.
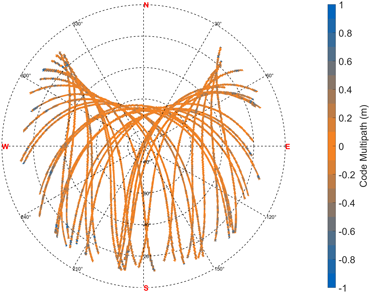
Fig. 4. CMGM of CCHJ station.
격자지도를 활용한 다중경로오차 보정 기법은 실시간 적용이 가능하다 (Fuhrmann et al. 2015, Lu et al. 2021). CMGM의 실시간 적용 방식을 반영하여 분석 날짜로부터 하루 전에 만들어진 CMGM을 목표 날짜의 관측데이터에 적용하여 성능 분석을 수행한다. Fig. 5는 본 연구에서의 CMGM 적용 방식을 나타낸다.
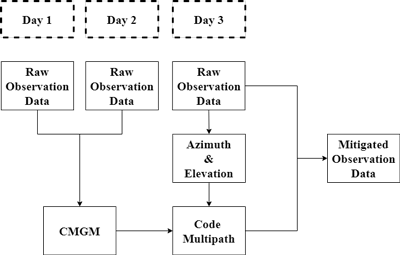
Fig. 5. CMGM application process in real-time.
충주(CCHJ), 어청도(EOCH), 안흥(ANHN), 소청도(SOCH) 기준국에 대하여 2023년 2월 7일을 분석 날짜로 설정하여 3종류의 Smoothing 기법과 3종류의 Gridding 기법에 따른 $AMP_i$의 RMS 변화량을 비교한 CMGM 성능 분석 결과는 Fig. 6과 같다.
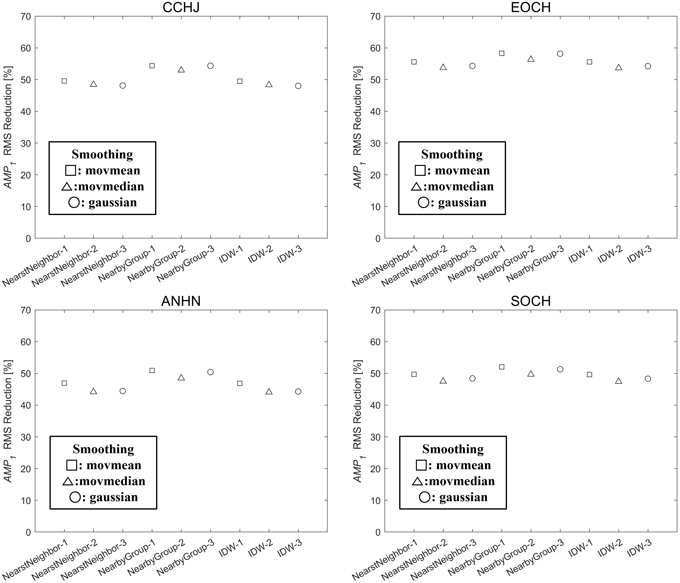
Fig. 6. Comparison of AMP1 RMS reduction percentage with different smoothing and gridding method of CMGM.
사각형, 삼각형, 원 기호는 각각 평균, 중앙값, 가우시안가중평균을 대표값으로 하는 Smoothing 기법을 의미한다. 모든 기준국에서 Gridding 기법에 따른 CMGM 성능 변화가 동일한 경향성을 보였으며 Nearest Neighbor 기법과 IDW 기법의 성능이 매우 유사하게 나타났다. Table 1은 각 기준국에서 가장 성능이 우수한 Smoothing & Gridding 조합과 그에 따른 $AMP_i$의 RMS 변화량을 나타낸 것이다. 모든 기준국에서 동일한 조합이 가장 우수한 성능을 나타냈으며 50%를 넘는 $AMP_i$ RMS 개선율을 보였다. 해당 결과를 바탕으로 추가적으로 수행한 성능 분석에서는 이동평균 Smoothing 기법과 Nearby Group 기법을 통해 생성한 CMGM을 사용하였다.
Table 1. Best combination of smoothing and gridding.
| Station | CCHJ | EOCH | ANHN | SOCH |
| Best combination | Movmean & Nearby group | Movmean & Nearby group | Movmean & Nearby group | Movmean & Nearby group |
| $AMP_i$ RMS reduction (%) | 54.3425 | 58.2541 | 50.8813 | 52.0457 |
충주(CCHJ), 어청도(EOCH), 안흥(ANHN), 소청도(SOCH), 말도(MLDO) 기준국에 대하여 2023년 2월 7일부터 2023년 2월 20일까지 2주동안 CMGM 성능 분석을 수행하였다. CMGM 적용 전후 AMP의 평균 RMS 변화량을 나타낸 결과는 Fig. 7과 같다.
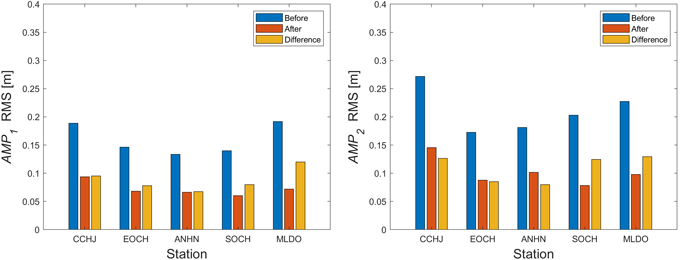
Fig. 7. RMS difference of AMP with CMGM multipath correction.
5개 기준국 모두 다중경로오차의 크기가 0.3 m 이내로 나타나는 것을 확인할 수 있고 다중경로오차의 보정효과는 0.1 m 내외로 나타나는 것을 확인할 수 있다. 일반적인 환경에서 코드 다중경로오차의 크기가 2~3 m (Subirana et al. 2013) 수준임을 고려할 때 기준국의 다중경로오차 환경은 매우 준수하다고 판단할 수 있으며 5개 기준국의 수신기와 안테나 사양이 모두 동일하므로 주변 지형의 차이가 크지 않다는 가정하에 다중경로오차의 크기가 비슷하게 나타난 것을 확인할 수 있다. 각 기준국에서 CMGM을 적용하기 전후의 $AMP$ RMS의 평균 변화량 및 감소율은 Table 2와 같다.
Table 2. AMP analysis results of CMGM.
| Station | CCHJ | EOCH | ANHN | SOCH | MLDO | |
| $AMP_1$ RMS | Before (m) After (m) Reduction (%) | 0.1887 0.0935 50.3886 | 0.1462 0.0684 53.1345 | 0.1336 0.0662 50.4445 | 0.1398 0.0601 56.9830 | 0.1917 0.0718 62.5072 |
| $AMP_2$ RMS | Before (m) After (m) Reduction (%) | 0.2717 0.1454 46.4084 | 0.1727 0.0877 49.1064 | 0.1814 0.1016 43.9599 | 0.2029 0.0783 61.3944 | 0.2273 0.0978 56.9407 |
5개 기준국 모두 40% 이상의 $AMP^{RMS}$ 감소율을 보였으며 감소율의 크기는 Lu et al. (2021)의 결과와 비슷하게 나타났다. $AMP_1$ 에서는 다중경로오차가 가장 큰 기준국인 말도 기준국에서 감소율이 가장 크게 나타났으며 해당 경향성은 Wang et al. (2020)의 결과와 일치했다. $AMP_2$ 에서는 다중경로오차의 크기가 중간 수준인 소청도 기준국에서 감소율이 가장 크게 나타났으며 해당 결과에 대해서는 다중경로오차의 차이가 뚜렷한 2개의 기준국을 새롭게 설정하여 추가적인 분석을 수행할 필요가 있다.
CMGM의 다중경로오차 보정 효과에 대한 파워 스펙트럼 분석 또한 수행하였는데, 2023년 2월 7일 말도 기준국에서 GPS PRN02에 대한 CMGM 적용 전후 $AMP$ 의 파워 스펙트럼 변화를 Fig. 8에 나타내었다.
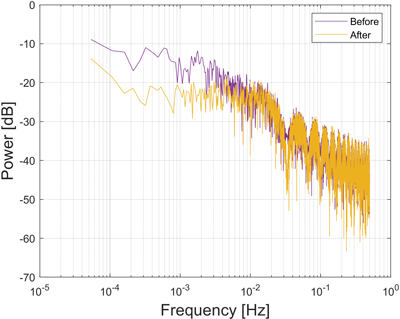
Fig. 8. Power spectral density of AMP with CMGM multipath correction.
Dong et al. (2016), Zheng et al. (2019), Wang et al. (2020)의 결과와 동일하게 0.05 Hz 미만의 저주파수 영역에서 CMGM을 통한 다중경로오차 보정의 효과가 두드러지게 나타나는 것을 확인할 수 있다.
SPP 성능 분석 환경은 $AMP$ 성능 분석 환경과 동일하게 설정했고, 본 연구에서의 SPP 수행을 위한 자료처리 전략은 Table 3과 같다.
Table 3. Data processing strategy for SPP.
| Parameters | Used in the study |
| Satellite signal Filtering Sampling interval Elevation cutoff Ionosphere correction Troposphere correction Satellite ephemeris/clock Stochastic model | GPS C1/P2 Weighted least square 1 sec 10˚ Ionosphere-free UNB 3 m Broadcast Satellite elevation weighting |
2주의 기간동안 CMGM 적용 전후 평균 수평/수직 위치오차의 변화를 나타낸 그래프는 Fig. 9와 같으며 2023년 2월 7일 말도 기준국에 대한 SPP 결과의 수평 위치 오차를 Fig. 10에 나타내었다.
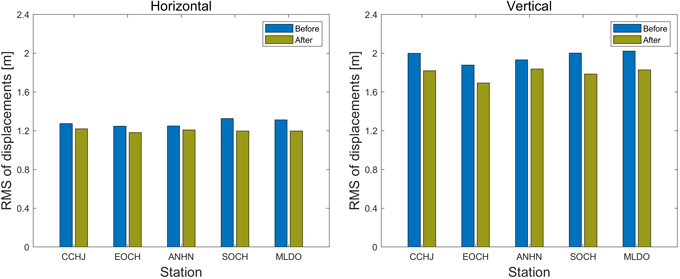
Fig. 9. RMS difference of GPS SPP solutions with CMGM multipath correction.
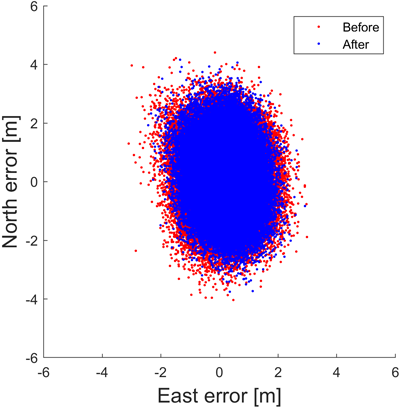
Fig. 10. Horizontal error of GPS SPP solution.
5개 기준국에 대해 수평과 수직 위치오차는 각각 평균 7%와 10% 수준의 RMS 감소율을 보였다. SPP 성능 분석에서의 위치오차 감소량의 크기는 $AMP$ 성능 분석에서의 다중경로오차 보정효과 크기와 유사한 0.1 m 내외로 나타났다.
본 연구에서 활용한 기준국보다 다중경로오차의 크기가 큰 기준국을 활용하거나 본 연구의 SPP 자료처리 전략에서 고려하지 않은 세부 오차요인들에 대한 모델링을 보강 후 SPP 성능 분석을 다시 수행한다면 CMGM 적용 전후 위치오차 개선율을 향상시킬 수 있을 것으로 예상된다.
본 논문에서는 국내 기준국 수신기의 1초간격 GPS 관측데이터로부터 CMGM을 생성한 후, 코드 다중경로오차 보정 정도 및 SPP 정확도 향상에 대한 CMGM의 성능 분석을 수행하였다. 5개 기준국에서 2주일의 기간(2023년 2월 7~20일)에 걸쳐 성능 분석을 수행한 결과, 본 연구에서 생성한 CMGM이 코드 다중경로오차 보정에 있어서 40% 이상의 효과를 나타내는 것을 확인하였다. SPP 정확도 향상에 있어서는 수평과 수직 위치오차에 대해 각각 평균 7%와 10%의 개선 효과를 나타내는 것을 확인하였다. 본 연구에서 생성한 CMGM을 활용하여 DGNSS, PPP-RTK와 같은 GNSS 보강시스템에 적용하여 성능향상에 대한 추가 분석을 수행할 예정이다.
Bilich, A. & Larson, K. M. 2007, Mapping the GPS multipath environment using the signal-to-noise ratio (SNR), Radio Sci., 42, RS6003. https://doi.org/10.1029/2007RS003652.
Caamano, M., Crespillo, O. G., Gerbeth, D., & Grosch, A. 2020, Detection of GNSS multipath with timedifferenced code-minus-carrier for land-based applications, in 2020 European Navigation Conference, Dresden, Germany, 23-24 November 2020, pp.1-12. https://doi.org/10.23919/ENC48637.2020.9317340
Dong, D., Wang, M., Chen, W., Zeng, Z., Song, L., et al. 2016, Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map, Journal of Geodesy, 90, 255-262. https://doi.org/10.1007/s00190-015-0870-9
Estey, L. & Wier, S. 2014, Teqc Tutorial: basics of Teqc use and Teqc products (Colorado, CO: UNAVCO Inc.), pp.1-61.
Fuhrmann, T., Luo, X., Knöpfler, A., & Mayer, M. 2015, Generating statistically robust multipath stacking maps using congruent cells, GPS Solutions, 19, 83-92. https://doi.org/10.1007/s10291-014-0367-7
García, V. P. & Woodhouse, N. 2020, Multipath Analysis Using Code-Minus-Carrier Technique in GNSS Antennas [Internet], available from: https://api.semanticscholar.org/CorpusID:220493648
Kee, C., & Parkinson, B. 1994, Calibration of multipath errors on GPS pseudorange measurements, In Proceedings of the 7th international technical meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, 20-23 Sep 1994, pp.353-362.
Lu, R., Chen, W., Dong, D., Wang, Z., Zhang, C., et al. 2021, Multipath mitigation in GNSS precise point positioning based on trend-surface analysis and multipath hemispherical map, GPS Solutions, 25, 111-122. https://doi.org/10.1007/s10291-015-0473-1
Subirana, J. S., Hernández-Pajares, M., & Zornoza, J. M. J. 2013, GNSS Data Processing, vol.1 (Cologne: ESA Communications).
Wang, Y., Zou, X., Deng, C., Tang, W., Li, Y., et al. 2020, A novel method for mitigating the GPS multipath effect based on a multi-point hemispherical grid model, Remote Sensing, 12, 3045. https://www.mdpi.com/2072-4292/12/18/3045
Yedukondalu, K., Sarma, A. D., & Vemuri, S. S. 2011, Estimation and mitigation of GPS multipath interference using adaptive filtering, Progress in electromagnetics research M, 21, 133-148. https://doi.org/10.2528/PIERM11080811
Zheng, K., Zhang, X., Li, P., Li, X., Ge, M., et al. 2019, Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning, Journal of Geodesy, 93, 2037-2051. https://doi.org/10.1007/s00190-019-01300-7
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2021R1I1A204882411), supported by the Space Challenge Program funded by the Korea government (MSIT) (NRF-2022M1A3B8073171), and was supported by Korea Research Institute for defense Technology planning and advancement (KRIT) grant funded by the Korea government (Defense Acquisition Program Administration, DAPA) (No. KRITCT-22-030, ReUSV-41, 2024).
Conceptualization, G. M. K. and G. K.; methodology, G. M. K. and G. K.; software, G. M. K.; validation, G. M. K., G. K., and C. P.; formal analysis, G. M. K., G. K., and C. P.; investigation, G. M. K. and G. K.; resources, G. M. K. and G. K.; data curation, G. M. K. and G. K.; writing—original draft preparation, G. M. K.; writing—review and editing, G. M. K., G. K., and C. P.; visualization, G. M. K.; project administration, G. M. K. and C. P.; funding acquisition, C. P.
The authors declare no conflict of interest.