Performance Analysis of a Vector Tracking Loop Receiver in RNSS with IGSO Satellite Visibility Variations

Technical Papers

Heesoo Jeong¹, Jae Hee Noh², Jin Seok Hong³, Gyu-In Jee^3,†

¹Electronic Information and Communication Engineering, Konkuk University, Seoul 05029, Korea ²Korea Aerospace Research Institute, Daejeon 34133, Korea
³Department of Electrical and Electronics Engineering, Konkuk University, Seoul 05029, Korea

^†Corresponding Author: Gyu-In Jee, E-mail: gijee@konkuk.ac.kr

Citation: Jeong, H., Noh, J.H., Hong, J.S., & Lee, G.-I. 2025, Performance Analysis of a Vector Tracking Loop Receiver in RNSS with IGSO Satellite Visibility Variations, Journal of Positioning, Navigation, and Timing, 14, 63-71.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 March, Volume 14, Issue 1, pages 63-71. https://doi.org/10.11003/JPNT.2025.14.1.63
Received on Dec 02, 2024, Revised on Dec 26, 2024, Accepted on Jan 18, 2025, Published on Mar 15, 2025.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Global Navigation Satellite System (GNSS) operates with 20 to 40 satellites while Regional Navigation Satellite System (RNSS) is served by approximately 10 satellites. Consequently, the limited number of satellites can adversely affect stand-alone positioning. To overcome this limitation, it is important to track as many satellites as possible for as long as possible. In this study, we introduce a vector tracking loop technique that utilizes strong signals to compensate for weak signals. However, during the vector tracking loop process, there is a possibility that a weak signal may negatively affect other signals. To address this problem, an adaptive covariance matrix was applied to optimize the tracking loop structure based on the residuals between the prediction phase and the actual measurements. For the extended QZSS (consisting of three GEO and four IGSO), we applied a minimum-angle criterion to analyze the visibility in a flat environment. By generating and processing signals under conditions of varying number of visible satellites, we found that the vector tracking loop outperforms the scalar tracking loop by more than 70% in reducing the Distance Root Mean Square (DRMS) when the signal is attenuated due to the decreasing elevation angle of the IGSO satellites.

KEYWORDS

vector tracking loop, adaptive noise variances, RNSS, IGSO

1. 서론

현대의 위치기반 서비스와 다양한 응용 분야에서 Global Navigation Satellite System (GNSS)는 필수적인 인프라이며, 이는 일상과 사회 전반에 걸쳐 중요한 역할을 하고 있다. GNSS 시스템의 이러한 중요성으로 인해 현재 전 세계 각국은 미국의 Global Positioning System (GPS)에 대한 의존도를 줄이고, 자국의 독자적인 GNSS 시스템을 구축하려는 노력을 하고 있다. 위성항법 시스템은 범지구적으로 서비스를 제공하는 GNSS와 특정 지역에 한정된 위치 서비스를 제공하는 Regional Navigation Satellite System (RNSS)로 서비스의 종류를 나눌 수 있다. Table 1에 정리된 각국의 위성항법 시스템을 살펴보면, GNSS는 국가별로 20 ~ 40개의 위성으로 전세계를 대상으로 서비스하고 있다. 반면에 RNSS는 국가별로 약 10개 내외의 위성으로 구성되어 있어 특정 지역에서의 정밀도 강화, 독립적인 위치 서비스가 필요할 때 사용되고 있다. 일본의 QZSS와 인도의 NavIC이 이에 해당된다. 특히, QZSS에서 사용되고 있는 Inclined Geosynchronous Orbit (IGSO) 위성은 높은 고도에서 8자 궤도를 따라 이동하며, 일본을 중심으로 아시아와 오세아니아 지역에 대한 신호의 가용성을 높이고 있다. 그러나 IGSO 궤도는 위성의 고도와 방위각이 지속적으로 변동되기 때문에 신호 품질에 영향을 줄 수 있다. 또한, IGSO 위성 신호의 Carrier to Noise Ratio (C/N₀)는 앙각이 높을 때는 안정적이나, 앙각이 낮은 기간 동안은 감소하는 경향이 있다 (Tan et al. 2022). 위성 수가 상대적으로 적은 RNSS 시스템을 단독으로 사용할 경우 더 쉽게 가시 위성 수가 4개 미만으로 줄어들어 위치 계산이 불가능하고, 가시 위성 수가 4개 이상으로 위치 계산이 가능하더라도 항법해의 정확도가 저하될 수 있다. 따라서 RNSS만으로 단독측위를 수행하는 환경에서는 더욱 강인한 신호 처리가 필요하다.

Table 1. Satellite constellation and features of navigation systems (NASA 2024).

Category	System	Number of satellites	Feature
GNSS	GPS	31 operational satellites	• Nearly 100% global coverage • 12-hour circular orbit, 20,200 km altitude
	GLONASS	26 satellites (24 operational, 2 in testing phase)	• Circular orbit, 19,140 km altitude
	Galileo	30 satellites (27 operational, 3 spares)	• Orbital planes at 23,222 km altitude
	BeiDou	35 satellites	• Walker constellation improves regional coverage • 5 GEO, 3 IGSO, 27 MEO
RNSS	QZSS	4 satellites	• Augments GPS for Asia Oceania with a focus on Japan • 3 IGSO, 1 GEO
RNSS	IRNSS (NavIC)	5 satellites	• Autonomous navigation for India • Geosynchronous orbits, apogee of 20,650 km

이 연구는 위성 신호를 더 강인하게 추적하기 위한 방법으로 vector tracking loop 기반의 소프트웨어 수신기를 이용했다. 사용한 vector tracking loop는 기존 연구와 차별화된 방식으로 추적과 항법을 각각의 Extended Kalman Filter (EKF)를 사용하여 계산한다. 이러한 방식으로 계산된 추적 및 항법 정보를 수신기 채널의 가시 위성 방향으로 투영하여 Delay Lock Loop (DLL)와 Phase Lock Loop (PLL)를 작동시키고 IGSO 위성 신호 추적 성능을 분석하였다. 특히, 신호가 약한 위성을 배제하지 않고 위성 신호를 보완하여 더 많은 위성을 이용하는 방식이 RNSS 환경에서 실질적인 이득이 있는지 검토하였다. 2장에서는 scalar tracking loop와 제안된 vector tracking loop의 구조를 나타내었고, 3장에서는 현재 운영 중인 QZSS보다 3개의 위성이 추가된 QZSS 신호를 상용 시뮬레이터를 활용하여 신호를 생성하였다. 생성된 신호에 대해 마스크 앵글(mask angle)을 설정한 지상 지역 환경에서 신호 추적 및 항법 성능을 비교하였다. 마지막으로 결과를 정리하였다.

2. TRACKING LOOP 구조 및 설계

2.1 Scalar Tracking Loop 구조

일반적으로 루프필터를 사용하는 기존의 GPS 수신기의 추적 방식인 scalar tracking loop는 여러 위성 신호가 입력될 때, 각 위성 채널 별로 신호를 독립적으로 추적하고 각 채널의 신호 추적 결과를 통해 항법해를 도출한다. 각 채널은 Fig. 1과 같이 상관기, 판별기, 루프필터, 수치 제어 오실레이터(Numerical Controlled Oscillator)로 구성된 별도의 피드백 루프를 통해 코드 위상과 도플러 주파수를 추적한다. 반송파 주파수를 검출하기 위해 PLL을 이용하며, 위성 신호의 추적을 위해 의사 거리 계산에 가장 중요한 요소인 코드 지연 값은 DLL을 이용한다. 이 구조는 구현이 간단하고 각 채널별로 독립적이기 때문에 신호를 병렬로 처리할 수 있다는 이점이 있다. 그러나 신호의 C/N₀가 약 30 dB-Hz 이하로 낮아진 환경에서는 추적 성능이 저하될 수 있다. 특히, scalar tracking loop에서는 각 위성 신호가 독립적으로 추적되므로 다른 위성의 정보를 활용한 보정이 어렵다. 이러한 한계를 개선하기 위해 2.2절에서 개별적인 채널 신호 추적 루프 대신 모든 채널에서 측정치와 추정오차를 추적 및 항법 필터로 전달하는 vector tracking loop를 구현하였다.

Fig. 1. Block diagram of scalar tracking loop without noise adaptive method.

2.2 Vector Tracking Loop 구조

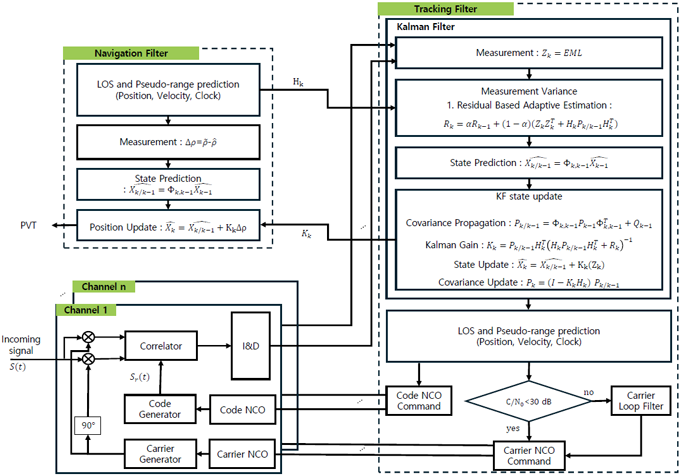
이 연구에서 구현한 vector tracking loop는 Fig. 2에 제시한 구조와 같이 추적 필터와 항법 필터로 구성되어 있다. 두 필터는 모두 EKF를 기반으로 설계되었으며, 서로 관측 행렬 H_k와 Kalman 이득 K_k을 공유한다. 추적 필터는 각 채널의 신호를 예측하는 역할을 담당하며, 공분산 예측, Kalman 이득 계산, 상태 갱신, 상태 공분산 갱신의 과정을 통해 필터 측정값을 갱신한다. 이후 갱신된 상태 변수는 코드와 반송파 주파수의 수치 제어 오실레이터 값을 결정하기 위한 커맨드 계산에 사용되며, 계산된 커맨드 값은 각 채널별 수치 제어 오실레이터로 전달된다. 반송파 주파수의 경우 기본적으로 scalar tracking loop와 유사하게 반송파 루프필터를 사용하여 수치 제어 오실레이터 커맨드 값을 결정하도록 구성되었다. 하지만 반송파 루프필터의 안정성을 보장하기 위한 C/N0 임계값이 27 ~ 30 dB-Hz (Morton et al. 2021)이므로 위성 신호의 C/N₀가 30 dB-Hz 미만인 경우에는 vector tracking loop로 계산된 커맨드 값을 적용한다. 반면에 항법 필터는 추적 필터에서 계산된 K_k를 이용하여 수신기의 위치와 같은 항법해만을 갱신한다. 실제로 수신기에 입력되는 신호에는 전리층 지연오차, 대류층 지연오차, 시계오차 등이 포함되어 있다. 추적 필터에서는 이러한 오차를 모두 포함하고 있는 신호를 예측하며, 이를 위해 측정치 Z_k로 Early-Minus-Late를 사용한다. 반면에 항법필터에서는 항법해의 정확도를 높이기 위해 전리층, 대류층, 시계오차 등이 제거된 신호를 예측하며, 이를 위해 관측된 의사거리 $\tilde{\rho}$ 와 상태 예측을 통해 계산된 의사거리 $\hat{\rho}$ 간의 차이를 측정치 $\Delta \rho$ 로 사용한다.

Fig. 2. Block diagram of vector tracking loop.

Vector tracking loop의 추적 및 항법 필터는 일반적인 scalar tracking loop의 루프필터와 유사하게 신호 추적에 필요한 상태를 예측하는 역할을 수행한다. 추적 및 항법 필터의 성능은 상태 변수에 따라 달라지며, 상태 변수의 차수는 루프필터 차수와 일치한다 (Song et al. 2013). 예를 들어, 필터의 상태 변수가 위치와 속도만을 포함한 모델인 경우, 위상과 주파수를 추적하는 2차 루프필터와 유사한 추적 성능을 제공하며, 상태 변수가 위치, 속도, 가속도까지 포함한 모델인 경우 위상, 주파수, 가속도를 추적하는 3차 루프필터와 유사한 추적 성능을 제공한다. 이 논문에서는 위치와 속도 모델로 Kalman 필터를 설계하여 상태 변수로 Eq. (1)과 같이 3차원 공간 상의 위치 오차 $\delta P_{3 \times 1}$ , 속도 오차 $\delta V_{3 \times 1}$ , , 수신기 시계 오차와 수신기 시계 오차 변화율 $\delta B_{2 \times 1}$ 를 사용한다. 이 상태 변수는 추적 필터와 항법 필터에 동일하게 사용하였다.

$X = \left[ \left( \delta P_{3 \times 1} \right)^T \, \left( \delta V_{3 \times 1} \right)^T \, \left( \delta B_{2 \times 1} \right)^T \right]^T$

Eq. (1)에서 정의한 상태 변수로부터 상태 방정식 $X_k$ 는 Eq. (2)와 같이 나타난다. 현재 상태 $k$ 에서 이전 상태 $k−1$ 을 기반한 상태 천이 행렬 $\Phi_{k, k-1}$ 은 Eq. (3)과 같이 나타낼 수 있으며, 상태 변수의 노이즈 특성을 나타내는 공분산 행렬 $Q_k$ 는 Eq. (4)로 정의된다 (Zhao & Akos 2011).

$X_k = \Phi_{k, k-1} X_{k-1} + \eta_{k-1}$

$\Phi_{k,k-1} = \begin{bmatrix} I_{3 \times 3} & \Delta t \cdot I_{3 \times 3} & 0_{3 \times 1} & 0_{3 \times 1} \\ 0_{3 \times 3} & I_{3 \times 3} & 0_{3 \times 1} & 0_{3 \times 1} \\ 0_{1 \times 3} & 0_{1 \times 3} & 1 & \Delta t \\ 0_{1 \times 3} & 0_{1 \times 3} & 0 & 1 \end{bmatrix}$

$Q_b = q_p \Delta t + \frac{1}{3} q_f \Delta t^3$

여기서 $η_{k−1}$ 는 공정 잡음, $\Delta t$ 는 항법해를 계산하는 주기, $I_{3 \times 3}$ 는 3차 단위 행렬, $q_d$ 는 가속도 잡음 공분산, $Q_b$ 는 시계 오차 잡음 공분산으로 Eq. (5)로 나타낼 수 있으며, $q_f \Delta t$ 는 시계 오차 변화율 잡음 공분산을 나타낸다. 또한, $q_p$ 는 속도와 관련된 잡음 모델링 요소, $q_f$ 는 가속도와 관련된 잡음 모델링 요소를 의미한다.

2.3 Noise Adaptive Method

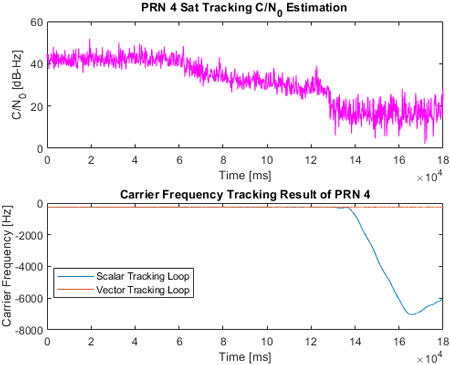
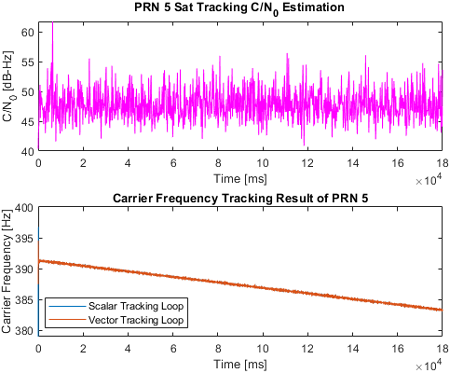
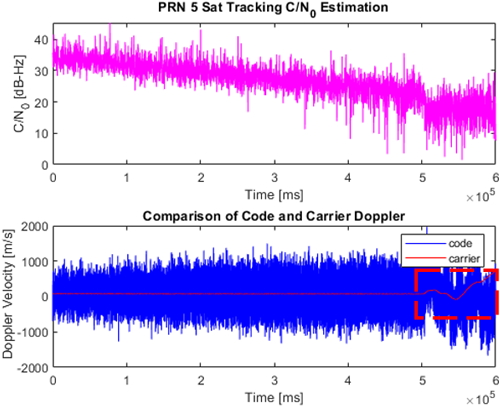
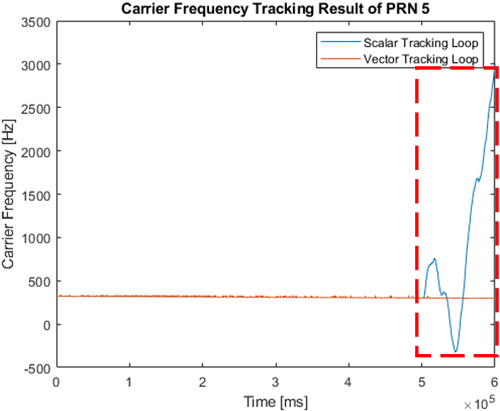
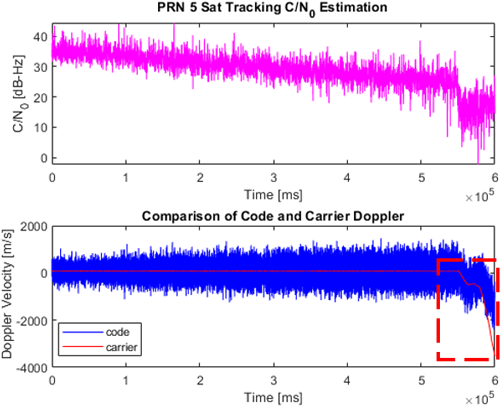
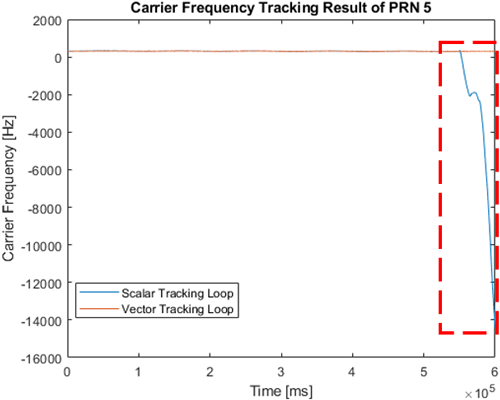
2.2절에서 구현한 vector tracking loop로 신호를 추적할 때 특정 위성 신호의 C/N₀가 크게 낮을 경우, 다른 위성 신호의 추적 성능까지 저하되는 문제가 발견되었다. 이를 검증하기 위해 PRN 1~7에 대한 180초 위성 신호를 생성하였으며, 초반 60초는 모든 신호를 감쇠 없이 생성하고, 후반 120초 동안은 PRN 4번 위성 신호의 세기만 감쇠하여 실험을 진행하였다. 이 신호 중 PRN 4번과 PRN 5번 위성 신호의 scalar tracking loop와 vector tracking loop로 처리한 시간 당 반송파 주파수 추적 결과는 Figs. 3과 4처럼 나타났다. scalar tracking loop로 처리한 PRN 5번 위성 신호는 반송파 주파수가 끝까지 수렴하지만, PRN 4번의 경우 신호 세기가 크게 감쇠되어 C/N₀가 약 27 dB-Hz 이하로 떨어졌을 때 반송파 주파수가 발산하는 것을 확인할 수 있다. 이처럼 각 위성에 대해 독립적으로 신호를 추적하는 scalar tracking loop 방식은 약한 세기의 신호의 영향 없이 안정적으로 반송파 주파수를 추적한다. Vector tracking loop로 처리된 PRN 4번 위성 신호의 반송파 주파수 추적 결과는 C/N₀가 약 27 dB-Hz 이하로 떨어진 이후 발산하는 것을 확인할 수 있으며, PRN 4번 위성 신호의 반송파 주파수가 발산하고 약 30초 후 PRN 5번 위성 신호의 반송파 주파수가 발산하는 것을 확인할 수 있다. 다른 위성에 대해 종속적으로 신호를 추적 및 항법해를 계산하는 vector tracking loop의 경우, 강한 신호가 약한 신호를 보정하여 가시 위성을 확보해야 하지만 Figs. 3과 4의 경우처럼 약한 신호가 다른 신호에 악영향을 미쳐 신호를 추적하지 못하는 상황이 일어날 수 있다.

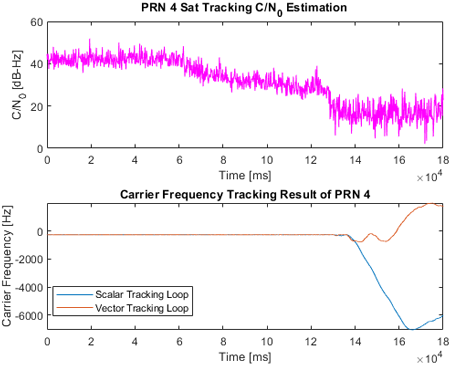
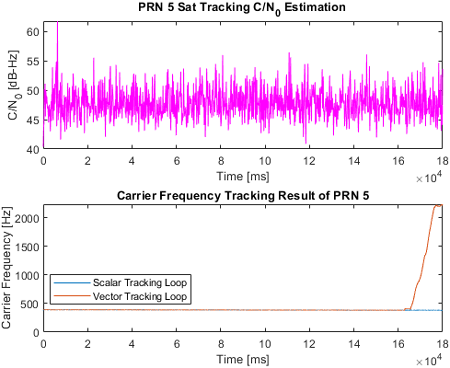
Fig. 3. Tracking result without noise adaptive method of PRN 4 satellite signal.

Fig. 4. Tracking result without noise adaptive method of PRN 5 satellite signal.

이를 방지하기 위해 측정 오차 공분산 행렬 $R_k$ 의 설계를 신중히 해야 한다. 측정 오차 공분산 행렬은 측정값의 신뢰도를 의미한다. $R_k$ 값이 크면 측정값의 신뢰도가 낮아 필터 업데이트 시 해당 채널의 측정값을 덜 반영하고, 반대로 신호 품질이 좋은 채널은 낮은 측정 오차 공분산 행렬을 갖기 때문에 상대적으로 더 많이 반영될 수 있다. 이 논문에서는 측정 오차 공분산 행렬을 예측 단계와 실제 측정치 간의 잔차를 이용한 적응적 공분산 행렬 방식으로 $R_k$ 를 Eq. (6)와 같이 계산하여 사용하였다.

$R_k = \alpha R_{k-1} + (1 – \alpha) \left( Z_k Z_k^T + H_k P_{k/k-1} H_k^T \right)$

여기서 α는 이전 상태에서 추정한 측정 오차 공분산 행렬인 $R_{k-1}$ 와 현재 상태의 정보의 가중치를 조절하기 위한 변수이며, 0<α<1의 값을 가질 수 있다. 또한, $Z_k Z_k^T$ 는 현재 상태의 잔차를 나타내고, $H_k P_{k/k-1} H_k^T$ 는 예측된 현재 상태의 공분산 행렬 $P_{k/k-1}$ 가 관측 행렬 $H_k$ 와 그의 전치행렬인 $H_k^T$ 를 통해 관측 공간에서 어떻게 표현되는지를 나타낸다. α의 값이 클수록 $R_{k−1}$ 를 더 많이 반영하게 되고 더 안정적인 $R_k$ 값을 얻을 수 있다. 하지만 잡음 변화에 둔할 수 있다. α의 값이 작아지면 현재 단계의 잔차가 더 크게 반영되어 더 빠르게 환경에 적응할 수 있지만 $R_k$ 값이 흔들릴 수 있다 (Akhlaghi et al. 2017). 이 논문에서는 α=0.9로 설정하여 시뮬레이션을 진행하였다. 이런 방식으로 계산된 $R_k$ 를 적용한 vector tracking loop로 위에서 사용한 신호를 처리한 결과는 Figs. 5와 6처럼 나타났다. $R_k$ 를 적용한 vector tracking loop로 처리된 PRN 4번과 PRN 5번 위성 신호의 반송파 주파수가 크게 오실레이션되지 않고 수렴하는 것을 확인할 수 있다. 결과적으로, Eq. (6)의 $R_k$ 를 이용하면 필터의 환경 적응성과 추정 정확도를 개선되어 약한 신호에 대한 안정적인 추적과 다양한 환경에서 신뢰도 높은 항법해를 계산이 가능하다.

Fig. 5. Tracking result with noise adaptive method of PRN 4 satellite signal.

Fig. 6. Tracking result with noise adaptive method of PRN 5 satellite signal.

3. 시뮬레이션

3.1 시뮬레이션 데이터 생성 및 처리 환경

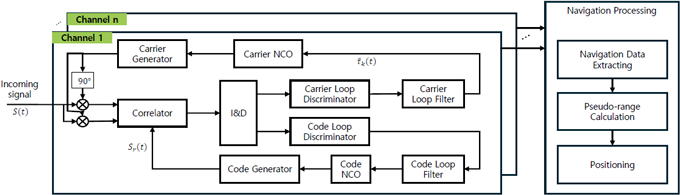
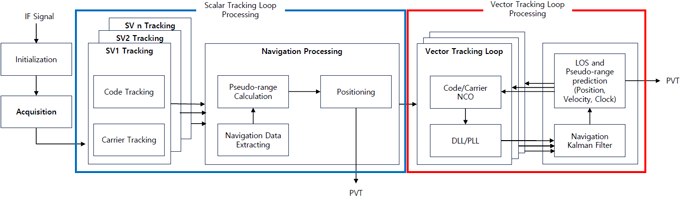
시뮬레이션에 사용된 신호는 Hong et al. (2024)에서 생성한 L2 대역의 GPS CNAV 신호를 기반으로 BOC(1,1) 변조 방식을 적용한 QZSS L2C/B 신호를 활용하였다. 이 연구에서 사용된 Software Defined Radio (SDR)는 Fig. 7에 나타난 것처럼 scalar tracking loop를 통해 신호 추적과 항법해를 계산한 후, EKF 기반의 vector tracking loop를 통해 신호를 처리하는 구조로 설계되었다 (Jeong et al. 2024). Vector tracking loop의 추적 필터가 신호를 예측하려면 먼저 항법해가 추정되어야 한다. 이를 위해 초기 단계에서 scalar tracking loop를 통해 신호 추적과 항법해 계산을 수행하도록 구성하였으며, 이 연구에서는 루프가 100번 반복될 때까지 scalar tracking loop 사용하여 초기 항법해를 결정하였다. Tracking loop의 구성은 2장에서 자세히 설명하였다.

Fig. 7. Processing of SDR.

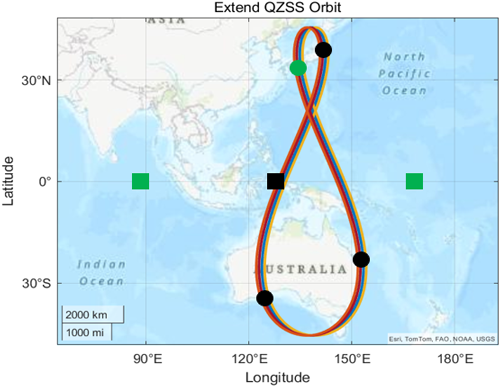
다양한 환경에서의 QZSS 단독 측위를 수행하기 위해 현재 GEO 1개와 IGSO 3개로 구성된 위성군이 아닌 Fig. 8과 같은 향후 구축될 GEO 위성 3개와 IGSO 위성 4개로 이루어진 QZSS 예상 위성군을 기준으로 QZSS L2C/B 신호를 만들었다. 이를 위해, 일본에서 제공하고 있는 4개의 QZSS 위성의 L2C 신호에 대한 RINEX 항법메시지 파일의 일부 항법 파라미터를 수정하여 GEO 위성 3개와 IGSO 위성 4개를 포함하는 새로운 항법 메시지 파일을 생성하였다. 신호의 제작과정은 Fig. 9에 나타낸 것처럼 7개 위성에 대한 RINEX 항법메시지 파일, CNAV 형식의 항법 메시지와 의사 잡음 코드를 Safran 사의 상용 GNSS 시뮬레이터인 Skydel에 입력하여 신호를 생성하였다. 이 시뮬레이터는 RINEX 항법메시지 파일을 활용해 위성의 궤도 움직임을 만들어내고, 설정한 변조 방식에 따라 설계된 항법 메시지와 PRN 코드를 삽입하여 IF 신호를 생성한다. 또한, 수신 안테나의 gain 패턴 모델 csv 파일로 입력할 수 있다 (Skydel 2024). 일반적으로 싱글 패치 안테나는 앙각이 ±50° 이상으로 넓게 퍼지는 방사 특성을 가지며, 이로 인해 저앙각에서는 위성의 신호 세기가 감소하여 천정 대비 10 ~ 20 dB 정도의 손실이 발생하는 경향이 있다. 특히, 앙각이 10도 보다 작을 경우 20 dB 이상의 큰 손실이 발생할 수 있다 (Zhou et al. 2024). 저앙각에서 위성 신호 세기가 감소하는 상황을 모델링하기 위해 마스크 앵글 이하의 위성 신호에는 싱글 패치 안테나의 방사 특성을 반영하여 10~20 dB의 추가 감쇠를 적용하였다.

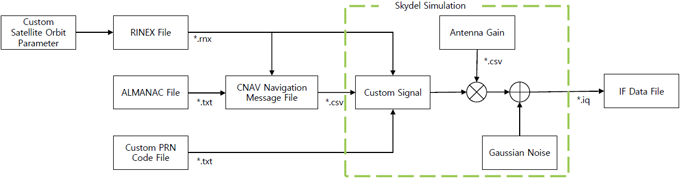
Fig. 8. Expected Quasi-geostationary orbit (Kishimoto et al. 2024).

Fig. 9. Generation processing of L2C/B custom signal.

위성의 앙각이 낮을수록 신호의 신뢰도가 떨어지기 때문에 GNSS 수신기는 일정 각도 이하의 앙각을 가진 위성을 제외하고 위치를 측정하며, 이 각도를 마스크 앵글이라고 한다. 이 논문에서는 일반적으로 평지에 위치한 사용자에 대한 항법 성능 평가에 사용되는 6.5°를 마스크 앵글 (Lee et al. 2005)으로 설정하였다. 이를 바탕으로, 한 위치에 고정된 사용자와 원운동을 하는 사용자에 대한 위성 신호를 생성하였다.

3.2 시뮬레이션 결과 분석

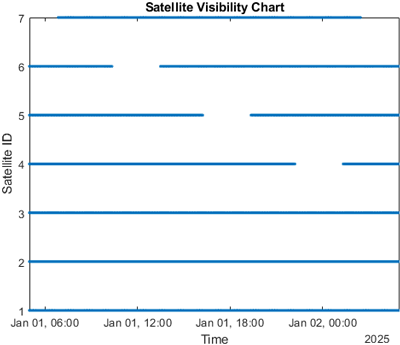
이번 절에서는 3.1절에서 제시한 방식으로 약 10분간 생성된 신호를 구현한 SDR을 이용해 항법 성능을 비교한다. 신호 생성 시 사용한 7개 위성의 RINEX 항법메시지 파일을 통해 24시간 동안 위도 37°, 경도 127°, 고도 2 m인 지점에서 최소 각 6.5° 기준으로 가시 위성을 분석한 결과는 Fig. 10에 나타나 있다. 분석 결과, 항상 6개 이상의 위성이 관측되었으며, 약 57.3%의 시간 동안은 6개의 위성, 약 43.7%의 시간 동안은 7개의 위성이 관측되는 것으로 확인되었다. 따라서 시뮬레이션은 7개의 가시 위성 중 1개의 IGSO 위성의 앙각이 낮아져 6개로 가시 위성이 줄어드는 상황을 기준으로 진행하였다.

Fig. 10. Result of skyplot for static receiver.

첫 번째로 위도 37°, 경도 127°, 고도 2 m인 지점에서 고정된 상태로 신호를 생성하고 처리하였다. 이때 Fig. 11의 scalar tracking loop로 추적한 PRN 5 (IGSO 위성)의 캐리어 주파수는 앙각이 감소하면서 신호의 C/N₀가 점차 떨어지면서 약 9분 이후에는 신호 추적이 불가능한 것을 확인할 수 있다. 반면, Fig. 12에서 vector tracking loop를 활용한 결과 끝까지 신호를 추적하는 것을 확인할 수 있다. 이러한 추적 신호를 기반으로 계산된 수신기 위치와 실제 수신기의 위치의 차이를 Fig. 13과 같이 나타냈다. Vector tracking loop로 얻은 항법해는 scalar tracking loop에 비해 변화가 크지 않고 일정하게 계산된다. Table 2에 제시된 Distance Root Mean Square (DRMS) 결과를 보면 오차의 평균은 scalar tracking loop를 통해 계산했을 때의 값이 더 작지만, 편차가 커 DRMS 값이 더 크게 나타나고 있다. Vector tracking loop를 이용해 신호를 처리한 경우 DRMS의 값은 0.825 m를 가지며, scalar tracking loop를 이용한 경우 DRMS의 값은 3.083 m이다. Vector tracking loop의 DRMS가 scalar tracking loop에 비해 약 73.2% 오차가 적게 나오는 것을 확인하였다.

Fig. 11. Scalar tracking loop results for static receiver.

Fig. 12. Carrier frequency tracking results of vector tracking loop and scalar tracking loop for static receivers.

Fig. 13. Positioning error results of NED coordinate system about static receiver.

Table 2. Static receiver’s DRMS results based on tracking loop type.

Tracking loop	Position error	N [m]	E [m]	D [m]	DRMS [m]
Scalar tracking loop	Mean	0.021	0.299	5.656	3.083
Scalar tracking loop	STD	2.61	1.616	4.212
Vector tracking loop	Mean	-0.546	0.338	5.345	0.825
Vector tracking loop	STD	0.459	0.238	0.535

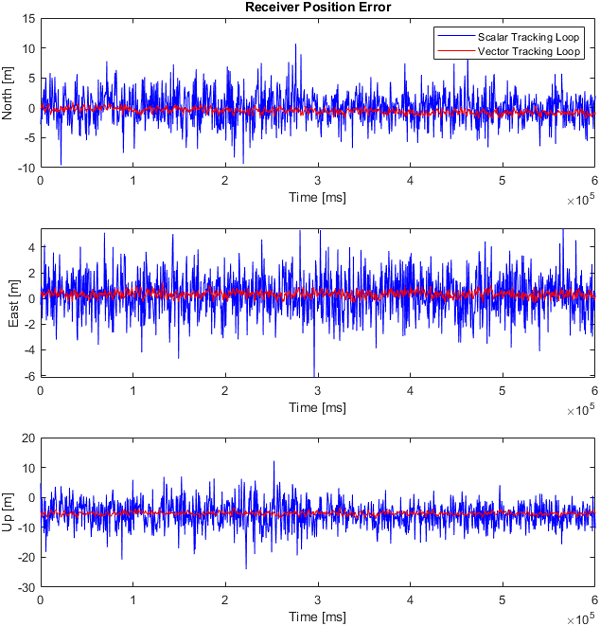
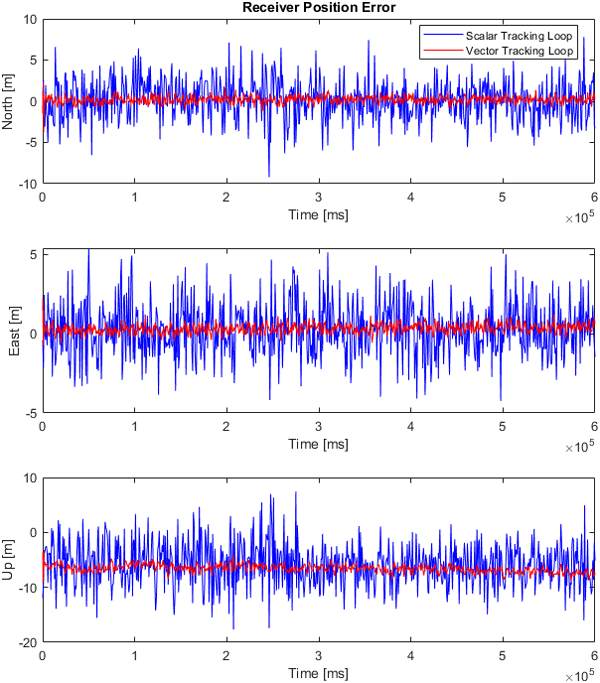
두 번째로 위도 37°, 경도 127°, 고도 2 m인 지점을 중심으로 반경 50 m로 원운동을 하는 상황에 대한 신호를 생성 및 처리하였다. Fig. 14의 결과처럼 SDR을 이용해 원운동의 항법해가 계산된 것을 확인할 수 있다. 고정된 수신기와 동일하게 원운동 역시 scalar tracking loop 방식으로 추적한 경우 신호 추적이 안되며 vector tracking loop로 처리했을 때만 신호가 끝까지 추적되는 것을 Figs. 15와 16을 통해 확인할 수 있다. Fig. 17과 Table 3에 제시된 DRMS 결과를 보면 원운동을 하는 수신자에 대해서도 고정된 수신자와 동일하게 vector tracking loop로 항법해를 구했을 때의 값이 더 고르게 나타나는 것을 볼 수 있고, 이로 인해 vector tracking loop를 이용했을 때의 DRMS 값은 0.601 m를 가지며, scalar tracking loop를 이용한 경우 DRMS의 값은 2.966 m이다. Vector tracking loop의 DRMS가 scalar tracking loop에 비해 약 79.7% 오차가 적게 나오는 것을 확인하였다.

Fig. 14. Positioning results in a map.

Fig. 15. Scalar tracking loop result for dynamic receiver.

Fig. 16. Carrier frequency tracking results of vector tracking loop and scalar tracking loop for dynamic receivers.

Fig. 17. Positioning error results of NED coordinate system about static receiver.

Table 3. Dynamic receiver’s DRMS results based on tracking loop type.

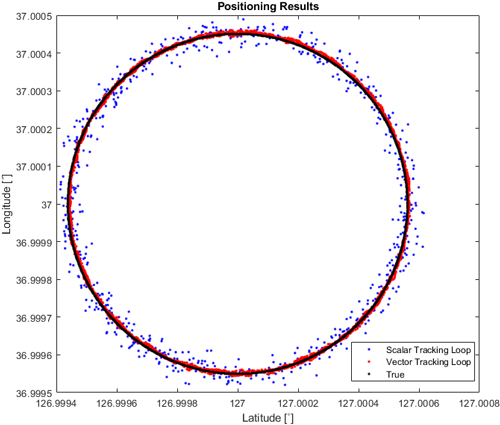
Tracking loop	Position error	N [m]	E [m]	D [m]	DRMS [m]
Scalar tracking loop	Mean	0.191	0.266	5.819	2.966
Scalar tracking loop	STD	2.41	1.701	3.984
Vector tracking loop	Mean	0.199	0.314	6.599	0.601
Vector tracking loop	STD	0.39	0.264	0.679

이번 장에서는 scalar tracking loop와 vector tracking loop의 성능을 고정된 수신기와 원운동을 하는 수신기 상황에서 시뮬레이션을 통해 비교하였다. 두 상황 모두에서 vector tracking loop가 품질이 낮은 위성 신호를 안정적으로 추적하며, 더 많은 위성 신호를 활용하여 정확한 항법해를 계산할 수 있는 것을 확인하였다. 특히 scalar tracking loop와 비교했을 때 DRMS 오차가 고정 상태에서 약 73.2%, 원운동 상태에서 약 79.7% 감소하는 결과를 통해 vector tracking loop의 강인한 항법 성능을 입증하였다.

4. 결론

이 연구에서는 기존 QZSS 위성군을 3개의 GEO 위성과 4개의 IGSO 위성으로 확장한 QZSS L2C/B를 단독으로 사용할 때, vector tracking loop와 scalar tracking loop를 이용한 항법성능을 비교 및 분석하였다. 특정 IGSO 위성이 관측자로부터 멀어지면서 신호 세기가 약해지는 상황에 대해 상용 위성항법 시뮬레이터로 신호를 생성하고, 구현한 vector tracking loop 기반 SDR 수신기로 처리하여 항법 성능을 평가 및 분석하였다. 실험 결과, 위성 신호의 C/N₀가 27 dB-Hz 이하로 감소할 경우 scalar tracking loop를 이용하면 해당 위성 신호의 반송파 주파수가 발산하는 것을 확인하였으며, vector tracking loop를 이용하면 신호의 반송파 주파수가 수렴하여 안정적으로 추적되는 것을 확인하였다. 또한, 신호의 세기가 약한 신호를 추적하여 항법해를 계산하는데 사용했을 때 약 73.2%와 약 79.7%의 DRMS 오차가 감소하는 성능 향상을 보였다. 추후 연구에서는 가시 위성 수에 변화를 주어 Dilution of Precision 관점에서의 이득에 대해 분석할 예정이다. 이를 통해 RNSS 환경에서 단독 측위를 수행할 때 항법 성능의 정확도를 개선할 수 있는 방안에 대해 연구할 계획이다.

ACKNOWLEDGEMENTS

이 연구는 Safran 사의 Skydel GNSS 시뮬레이터를 활용하여 진행되었으며, 이에 대한 지원에 감사를 드립니다.

AUTHOR CONTRIBUTIONS

Conceptualization, Jeong, H. and Jee, G.-I.; methodology, Jeong, H., Hong, J. S., and Jee, G.-I; software, Jeong, H., Hong, J. S., and Jee, G.-I.; validation, Jeong, H.; formal analysis, Jeong, H. and Hong, J. S.; investigation, Jeong, H., Hong, J. S., and Jee, G.-I.; resources, Jeong, H., Noh, J. H., and Jee, G.-I.; data curation, Jeong, H. and Hong, J. S.; writing—original draft preparation, Jeong, H.; writing—review and editing, Jeong, H., Noh, J. H., Hong, J. S., and Jee, G.-I.; visualization, Jeong, H. and Hong, J. S.; supervision, Jee, G.-I.; project administration, Jee, G.-I.; funding acquisition, Noh, J. H. and Jee, G.-I.

CONFLICTS OF INTEREST

The authors declare no conflict of interest.

REFERENCES

Akhlaghi, S., Zhou, N., & Huang, Z. 2017, Adaptive Adjustment of Noise Covariance in Kalman Filter for Dynamic State Estimation, 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA 16-20 Jul 2017. https://doi.org/10.1109/PESGM.2017.8273755

Hong, J. S., Jeong, H., & Jee, G.-I. 2024, Analysis of the Navigation Performance of Additional L2C BOC(1,1) Signal in the Extended QZSS Constellation, 2024 IPNT Conference, Jeju, Korea, 6-8 Nov 2024, pp.137-140. https://ipnt.or.kr/2024proc/167

Jeong, H., Hong, J. S., & Jee, G.-I. 2024, Implementation of IGSO Signal Processing SDR Based on Vector tracking loop, 2024 IPNT Conference, Jeju, Korea, 6-8 Nov 2024, pp.517-519. https://ipnt.or.kr/2024proc/179

Kishimoto, M., Sakai, Y., Hosoda, S., Yamane, T., & Numata, K. 2024, QZSS Latest Status, Pacific PNT, Honolulu, Hawaii, 15-18 Apr 2024. https://www.ion.org/pnt/ abstracts.cfm?paperID=13086

Lee, S.-H., Park, B.-W., Kim, D.-Y., Kee, C.-D., Paik, B.-S., et al. 2005, Orbit Design of a Korean Regional Communication & Navigation Satellite System, JKSAS, 33, 51-58. https:// doi.org/10.5139/JKSAS.2005.33.7.051

Morton, Y. J., van Diggelen, F., Spilker, J. J., & Parkinson, B. W. 2021, Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications, vol.1 (Hoboken, New Jersey: Wiley-IEEE Press).

National Aeronautics and Space Administration (NASA), Global Navigation Satellite System Overview [Internet], cited 2024 Mar 14, available from: https://cddis.nasa. gov/Techniques/GNSS/GNSS_Overview.html

Skydel, Skydel Custom Signal documentation, [Internet], cited 2024 Sep, available from: https://safrannavigation-timing.com/manuals/skydel/Content/SDX/ Intro/Home_Page.htm

Song, J.-H., Im, S.-H., & Jee, G.-I. 2013, Performance Evaluation of Vector tracking loop Based Receiver for GPS Anti-Jamming Environment, Journal of Institute of Control, Robotics and Systems, 19, 152-157. https://doi. org/10.5302/J.ICROS.2013.19.2.152

Tan, B., Ai, Q., & Yuan, Y. 2022, Analysis of Precise Orbit Determination of BDS-3 MEO and IGSO Satellites Based on Several Dual-Frequency Measurement Combinations, Remote Sens., 14, 6030. https://doi. org/10.3390/rs14236030

Zhao, S. & Akos, D. 2011, An Open Source GPS/GNSS Vector tracking loop – Implementation, Filter Tuning, and Results, Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, 24-26 Jan 2011, pp.1293-1305. https://www.ion.org/ publications/abstract.cfm?articleID=9580

Zhou, Z., Shi, J., Liu, G., Xu, K., & Jiang, R. 2024, A Bidirectional Quasi-Endfire Patch Antenna with Low Elevation Angle, Micromachines, 15, 777. https://doi. org/10.3390/mi15060777

ABSTRACT
KEYWORDS
1. 서론
2. TRACKING LOOP 구조 및 설계
3. 시뮬레이션
- 3.1 시뮬레이션 데이터 생성 및 처리 환경
- 3.2 시뮬레이션 결과 분석
4. 결론
ACKNOWLEDGEMENTS
AUTHOR CONTRIBUTIONS
CONFLICTS OF INTEREST
REFERENCES

Journal of Positioning, Navigation, and Timing (J Position Navig Timing; JPNT)

Indexed in KCI (Korea Citation Index)

OPEN ACCESS, PEER REVIEWED

pISSN 2288-8187 eISSN 2289-0866

Technical Papers