Soyoon Yoon, Yongrae Kim, Jeongrae Kim†
Department of Aeronautical and Astronautical Engineering, Korea Aerospace University, Gyeonggi-do 10540, South Korea
†Corresponding Author: Jeongrae Kim, E-mail: jrkim@kau.ac.kr
Citation: Yoon, S., Kim, Y., & Kim, J. 2025, Prediction Method of F10.7 Solar Radio Flux with the ARMA and the LSTM Models, Journal of Positioning, Navigation, and Timing, 14, 37-46.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 March, Volume 14, Issue 1, pages 37-46. https://doi.org/10.11003/JPNT.2025.14.1.37
Received on Jan 25, 2025, Revised on Feb 10, 2025, Accepted on Feb 13, 2025, Published on Mar 15, 2025.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The ranging error of the global navigation satellite system (GNSS) caused by the ionosphere significantly degrades GNSS positioning accuracy. Correcting and predicting ionospheric delay is thus important for improving GNSS accuracy. The ionospheric delay mainly depends on solar activity. Accurate prediction of the F10.7 index, an essential indicator of the intensity of solar activity, is required to accurately predict the global ionospheric delay. Two time series forecasting algorithms have been developed for the F10.7 prediction in this study: the auto-regressive moving average (ARMA) model and the long short-term memory (LSTM) model. The predictions were performed for one-day and seven-days ahead data. The LSTM model was trained with 45 years of data and the ARMA model was trained with 270 days of data. For the one-day prediction, both the ARMA and LSTM methods yielded a low prediction error, less than 2.1% of the true F10.7 value. But for the seven-day prediction, the LSTM method yielded a lower level of prediction error, 7.1%, than the ARMA method.
F10.7, ARMA, LSTM, time series forecasting, GNSS, GPS
우주기상은 지구와 우주 환경 간의 상호작용으로 발생하는 다양한 현상을 포함하며, 위성항법시스템 (Global Navigation Satellite System, GNSS)의 성능에 중요한 영향을 미친다. 특히 태양 활동은 전리층의 총 전자량 (Total Electron Content, TEC)에 영향을 미치며 GNSS 신호의 지연과 위치 오차를 유발하는 주요 요인으로 작용한다 (NOAA 2024a). 일반적으로 태양 활동이 활발할수록 전리층 지연 오차와 사용자 위치 오차가 증가한다. 태양 활동의 주요 지표로는 F10.7 태양활동지수가 사용되며, 이는 태양에서 방출되는 2.8 GHz 대역 (10.7 cm 파장)의 태양 복사 강도를 나타낸다 (Tapping 2013). 태양 활동은 약 11년을 주기로 극대기와 극소기를 반복하는데, 극대기에는 태양 활동이 활발해져 더 많은 태양 복사선이 방출되고, 극소기에는 태양 활동이 감소하며 방출량도 줄어드는 경향을 보인다 (NOAA 2024b, 2024c).
전리층 지연 오차를 보정하기 위해 Global Positioning System (GPS)은 항법메시지를 통해 Klobuchar 전리층 모델 정보를 제공하여 사용자가 전리층으로 인한 신호 지연 오차를 보정할 수 있도록 한다. Klobuchar 모델은 전리층에 의한 신호 지연의 강도와 지속시간을 8개의 계수로 표현하여 GPS 신호 지연을 보정하는 방식이다. 이 모델은 하루 단위로 갱신되는 예측 정보를 기반으로 실시간 전리층 지연값 대신 1일 후의 예측 지연값을 생성한다. Klobuchar 모델은 전리층 지연값을 예측하기 위해 주로 F10.7 태양활동지수의 예측값을 활용하는 것으로 알려져 있다 (Klobuchar 1987). F10.7과 연중 날짜 (day of year)를 입력모델로 하는 경험모델을 이용하여 F10.7 예측값에 따라 미리 정해진 Klobuchar 모델 파라미터값을 전송하는 방식이다. 따라서 F10.7 예측 정확도를 향상시키는 것은 GPS Klobuchar 모델 또는 유사한 전리층 모델의 성능을 높이는 데 매우 중요하다. 장기간 Klobuchar 전리층모델의 정확도를 분석한 연구에서 Klobuchar 모델의 전리층 보정오차와 F10.7값은 0.85의 높은 상관관계를 가지는 것으로 파악되었다 (Kim & Kim 2023).
F10.7 예측에 관한 연구는 이전부터 활발히 이루어져 왔다. 시계열예측에 많이 사용되는 AutoRegressive (AR), Auto-Regressive Integrated Moving Average (ARIMA) 모델, Support Vector Regression (SVR)와 같은 회귀 (Regression) 모델을 활용한 연구들이 대표적이다. Du (2020)는 AR 모델을 사용하여 1일부터 81일까지 예측을 수행하였으며, 예측기간별로 다른 최적화 파라미터를 적용하여 최적의 차수를 탐색하였다. Liu et al. (2010)과 Wen et al. (2010)은 AR 모델을 사용하여 최대 27일까지의 예측을 수행하였다. 머신러닝 모델을 기반으로 한 F10.7 예측 연구가 활발히 진행되고 있는데, Chatterjee (2001)는 neural network을 사용하여 1일 예측을 수행하였으며, Huang et al. (2009)은 SVR 모델로 11년간 데이터를 사용하여 3일이내 예측을 수행하였다. Long Short-Term Memory (LSTM) 네트워크는 시계열 예측에 적합한 모델로 주목받아 다양한 연구에 활용되고 있다. Kim et al. (2020)은 ARIMA와 LSTM을 사용한 연구를 수행하였는데, 월평균 F10.7 데이터를 사용하여 12개월까지 월 단위 예측을 수행하였다. Zhang et al. (2022) 역시 LSTM 모델을 사용하여 F10.7 데이터를 최대 3일까지 예측하였다. 기존 LSTM 모델을 확장한 기법도 개발되고 있는데, Luo et al. (2022)는 Convolutional Neural Network (CNN)에 LSTM을 결합하였으며, Hao et al. (2024)는 Variational Mode Decomposition (VMD)에 LSTM을 결합하여 F10.7 예측을 수행하였다. F10.7과 유사한 성향을 나타내는 태양흑점수(Sun Spot Number, SSN) 예측에 관한 연구도 많이 수행되었는데, Abdel-Rahman & Marzouk (2018)는 AR과 ARIMA 모델을 이용하여 2년간 SNN을 예측하였다.
본 연구에서는 시계열 데이터 예측에 널리 사용되는 Auto-Regressive Moving Average (ARMA) 모델과 LSTM 모델을 이용하여 F10.7 예측 기법을 개발하고, 두 모델의 예측 성능을 비교하였다. ARMA 모델은 일반적으로 LSTM 모델에 비해 장기 예측 성능이 부족하지만, 구현이 간단하고 성능 최적화가 용이하여 안정성이 중요한 예측 시스템에는 적합할 수 있다. 반면, LSTM 모델은 복잡한 시계열 데이터를 처리하는 데 강점을 가지며, 보다 정확한 예측이 가능하다. 추가적으로, ARMA 및 LSTM 모델과의 성능 비교를 위해 다항식 외삽법과 같은 간단한 예측 기법도 적용하였다. 기존의 연구들은 주로 1개월에서 12개월까지의 중장기 예측을 목표로 하였으나, 본 연구는 위성항법 전리층 보정 정보 생성에 사용되는 것을 주요 목적으로 하기 때문에 예측 기간을 1일부터 7일까지로 짧게 설정하였다. 이는 Klobuchar 모델을 사용하여 다음 날 또는 일주일 후의 전리층 지연값을 예측하는 것을 가정한 설정이다. 새로운 예측기법을 제시하는 기존 논문에 비해 본 연구는 추정 파라미터의 최적화에 주안점을 두었다. 최적화 파라미터는 예측기간에 따라 변하게 되는데 중장기 예측을 목표로 하는 기존 연구에 비해 7일 이내의 짧은 예측기간에 적합한 최적화 파라미터를 제시하였다.
F10.7 예측에서는 다양한 우주환경 변수들을 활용할 수 있지만, 본 연구에서는 과거 F10.7 값만을 사용하여 예측을 수행하였다. LSTM 모델은 학습 데이터의 길이가 예측 성능에 중요한 영향을 미치므로, 태양 활동의 약 11년 주기 변화를 고려해 이를 초과하는 장기간의 데이터를 사용하는 것이 필요하다. 또한, 태양 활동은 각 주기마다 강도가 달라지는 특성이 있으므로, 본 연구에서는 1965년부터 2009년까지 총 45년간의 데이터를 학습에 사용하고, 2010년부터 2020년까지의 11년 데이터를 예측하여 검증하였다. ARMA 모델은 사용한 차수에 따라 학습길이를 결정하는데, 본 연구에서는 270일 학습데이터를 사용하였으며, 학습길이 결정 방법은 3.2절에 기술하였다.
이 논문의 2장에서는 F10.7 예측기법의 이론에 관해 설명하고, 3장에서는 예측에 사용한 데이터와 데이터 전처리 과정에 관하여 설명하였다. 4장에서는 예측 모델의 최적화와 학습 방법을 설명하고, 5장에서 예측결과의 성능분석을 수행하였다.
ARMA 모델은 자기회귀 모델인 AR 모델과 이동평균 모델인 Moving Average (MA) 모델을 결합한 모델이며, 시계열데이터를 예측하는데 많이 사용된다 (Box & Jenkins 1970). 식 (1)은 미래의 시계열데이터
y
(
t
)
를 예측하는 ARMA 모델의 식을 나타내고 있다.
수식
여기서
T
는 시계열데이터 샘플링 간격이며,
y
(
t
−
k
T
)
는 과거 데이터를 의미한다. 오차
u
(
t
)
는 백색 잡음 (white noise)이다. AR 모델은 과거 데이터의 가중치 합으로 구성되며, MA 모델은 오차의 가중치 합으로 구성된다.
p
와
q
는 각각 AR 모델과 MA 모델의 차수이다. 입력 시계열데이터에 대한 ARMA 모델을 구성하는 것은 AR계수
A
k
와 MA 계수
B
k
를 결정하는 것을 의미하는데, 최소자승법 및 Yule-Walker 모델 등 다양한 결정방법이 개발되어 왔다 (Yule 1927, Box & Jenkins 1970). 과거 데이터를 많이 사용할수록 예측 정확도는 증가하지만, 일정 수준을 넘어 차수
p
와
q
가 과도하게 크다면 모델의 복잡성과 과적합의 가능성이 증가한다 (Hyndman & Athanasopoulos 2021). Fig. 1은 AR 모델과 MA 모델로 구성된 ARMA 모델의 구조를 나타내고 있다.
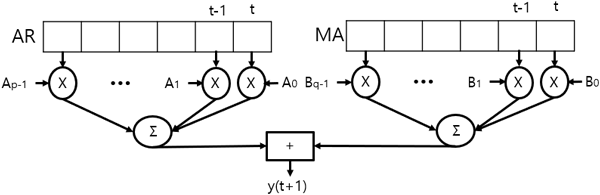
최적화된 ARMA 모델의 계수
A
k
와
B
k
를 선정하기 위한 지표로 많이 사용되는 것은 Akaike’s Information Criterion (AIC)인데, 이는 예측값의 적합도를 나타내는데 사용되는 것으로, ARMA 차수에 대한 패널티를 적용한 AIC는 식 (2)와 같이 나타낼 수 있다 (Akaike 1974).
수식
여기서
^
σ
는 예측값 오차의 표준편차,
n
은 최소 시계열 데이터 길이로, AIC는 예측값의 잔차 및 ARMA 모델에 사용된 계수의 개수로 구성된다. 예측오차와 추정 매개변수 수를 더하여 모델의 적합도 평가하면서 복잡성도 동시에 고려하여, 최적의 모델을 선택할 수 있다. AIC 값이 최소가 될 경우 예측에 가장 적합한 모델이다. AIC와 병행하여 예측값의 Root Mean Squared Error (RMSE)도 사용하였다.
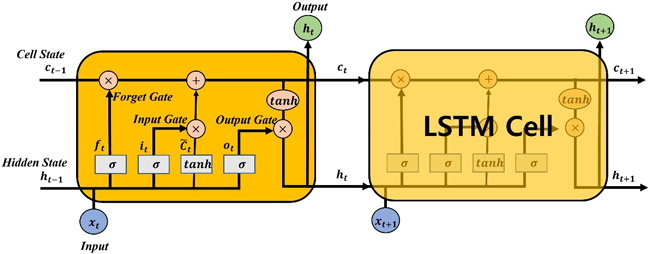
LSTM 네트워크는 Recurrent Neural Network (RNN)에서 발생하는 장기 종속성 문제를 해결하기 위해 개발된 딥러닝 기법 중 하나이다 (Hochreiter & Schmidhuber 1997). RNN은 장기 데이터를 학습할 때 역전파 과정에서 기울기가 소실되는 문제가 발생하여 가중치 갱신이 제대로 이루어지지 않는 한계를 가진다. 이러한 문제를 해결하기 위해 LSTM 네트워크는 입력 게이트, 망각 게이트, 출력 게이트를 활용하여 RNN의 은닉 상태에서 셀 상태를 제어한다. Fig. 2에 나타난 LSTM 구조는 각 게이트가 현재 입력과 이전 네트워크 출력을 결합하여 게이트 출력을 계산하며, 이는 식 (3)과 같이 표현된다 (Cui et al. 2018).
수식
여기서
W
x
와
W
h
는 각각 현재 입력
x
t
와 이전 출력
h
t
−
1
의 가중치를 나타내며,
b
f
는 망각 게이트의 편향을 의미한다.
σ
는 활성화 함수로, 망각 게이트에서는 주로 시그모이드 함수가 사용된다. 여기서
f
t
는 망각 게이트의 출력값으로, 셀 상태
c
t
−
1
에서 어떤 정보를 잊을지를 결정한다.
f
t
의 값이 0에 가까우면 해당 정보를 완전히 잊고, 1에 가까우면 정보를 그대로 유지한다. 망각 게이트는 네트워크가 학습 중에 필요하지 않은 정보를 제거함으로써 셀 상태를 효율적으로 관리할 수 있도록 돕는다.
입력 게이트는 현재 입력과 과거 셀 상태를 기반으로 작동하며, 새로운 셀 상태
c
t
는 망각 게이트의 출력과 과거 셀 상태의 곱, 그리고 입력 게이트 출력과 입력 정보의 곱의 선형 결합으로 계산된다. 이를 수식으로 나타내면 식 (4)와 같다.
수식
여기서
i
t
와
g
t
는 각각 sigmoid 함수와 hyperbolic tangent 함수에 의해 계산된 입력 게이트의 출력이다.
i
t
는 새로 추가할 정보를 결정하고,
g
t
는 현재 입력의 새로운 후보 값이다.
마지막으로, 네트워크의 최종 출력 상태
h
t
는 출력 게이트의 출력 값과 현재 셀 상태의 결합으로 식 (5)와 같이 계산된다.
수식
여기서
o
t
는 출력 게이트의 출력으로, 현재 입력
x
t
, 이전 출력
h
t
−
1
, 그리고 셀 상태와 결합하여 sigmoid 함수로 계산된다. 출력 게이트는 네트워크가 셀 상태의 정보를 얼마나 외부로 전달할지를 결정하며, 이는 식 (6)으로 표현된다.
수식
여기서
W
x
o
와
W
h
o
는 출력 게이트의 가중치,
b
o
는 출력 게이트의 편향을 나타낸다. 출력 게이트의 활성화 값
o
t
는 현재 셀 상태
c
t
에 hyperbolic tangent 함수
tanh
(
c
t
)
를 곱하여 최종 출력 상태
h
t
를 생성한다.
LSTM 네트워크는 시계열 데이터 처리와 예측 문제에서 매우 우수한 성능을 보이는 RNN 구조이다. 본 논문에서 사용된 LSTM 구조는 LSTM 계층과 완전 연결 (fully connected) 계층으로 구성되며, F10.7 태양활동지수를 입력 데이터로 활용한다. 입력 데이터는 LSTM 계층을 통과한 후, 완전 연결 계층에서 최종 네트워크 출력이 계산된다. 이를 통해 현재의 F10.7 데이터를 기반으로 k 시점 이후의 데이터를 효과적으로 예측할 수 있다.
ARMA 모델과 LSTM 모델의 성능 비교를 위하여 예측 모델에 다항식 외삽법 (polynomial extrapolation)을 함께 사용하였다. 다항식 외삽법은 시계열 데이터에서 과거의 데이터를 기반으로 다항식을 생성하여 외삽값을 예측하는 방법이다. 식 (7)과 같이 표현하며, 다항식 차수 n을 결정한 후 (n+1)개의 데이터를 기반으로 계수
a
i
를 결정하여 외삽값을 예측한다.
수식
여기서
x
i
는 입력값이며,
y
는 모델에 의해 추정되는 외삽값에 해당된다.
Bayesian 최적화는 특정 파라미터
x
에 대한 목적 함수
y
=
f
(
x
)
의 값을 최소화하기 위한 효율적인 방법으로 최적화기법에서 많이 사용되는 일반적인 방법이다. 본 연구에서는 최적화과정에서 조정해야 하는 파라미터 수가 많은 LSTM에 Bayesian 최적화기법을 적용하였다. 본 연구에서는 LSTM 모델의 RMS 오차를 목적 함수
y
로 정의하였으며, RMS 오차를 최소화하는 hyper parameter 조합을 찾는 것을 목표로 하였다. Bayesian 최적화는 Bayes 정리에 기반하고 있으며, Bayes 정리는 사전 확률과 관측된 데이터를 이용하여 사후 확률을 계산하는 이론이다. 이는 식 (8)과 같이 표현된다.
수식
여기서
P
(
A
|
B
)
는
B
가 주어졌을 때
A
가 발생할 확률, 즉 조건부 확률을 의미하며,
P
(
B
|
A
)
는
A
가 주어졌을 때
B
가 발생할 확률이다. 또한,
P
(
A
)
는 사건
A
의 사전 확률,
P
(
B
)
는 사건
B
의 전체 확률을 나타낸다.
Bayesian 최적화는 초기 탐색, 사후분포 업데이트, 그리고 획득 함수 최적화의 세 단계로 이루어진다. 첫 번째 단계에서는 설정된 변수 범위 내에서 임의의 점
x
i
를 선택하고, 이 점에서 목적 함수
y
i
=
f
(
x
i
)
를 계산한다. 두 번째 단계에서는 초기 탐색에서 계산된 데이터
x
i
와
y
i
를 바탕으로 목적 함수의 사후분포
Q
(
f
|
x
i
,
y
i
)
를 Gaussian Process로 모델링하여 업데이트한다. 세 번째 단계에서는 사후분포를 기반으로 획득 함수
a
(
x
i
)
를 최적화하여 다음 탐색 지점
x
i
+
1
을 선택한다. 획득 함수는 사후분포로부터 점
x
i
의 적합도를 평가하며, 탐색 과정에서 이미 조사된 영역의 점들을 과도하게 조사하지 않도록 설계되었다. 이를 통해 전역 최적해 (global minimum)를 찾을 가능성을 높이고, 지역 최적해 (local minimum)에 머무르는 문제를 방지한다 (Snoek et al. 2012). 이처럼 Bayesian 최적화 기법은 random search, grid search 방법과 비교하여 hyper parameter 공간을 보다 효율적으로 탐색할 수 있도록 한다.
본 연구에서는 독일 GeoForschungsZentrum (GFZ)에서 제공하는 1일 단위의 F10.7 관측 데이터를 사용하였으며 (GFZ 2024), 1965년부터 2020년까지의 56년치 데이터를 학습과 예측 검증에 활용하였다. 일반적으로 1개월 이상의 장기 예측에서는 월 평균 데이터와 같은 1개월 단위 데이터를 사용하는 경우도 있으나, 본 연구는 1일에서 7일까지의 단기 예측에 주목하여 1일 단위 데이터를 사용하였다. 한편, 특정일의 데이터가 누락될 경우, 연속적인 시계열 데이터를 가정하는 예측 알고리듬의 구동에 문제가 발생할 수 있다. 56년간 20,454개 데이터 중 누락된 데이터의 개수는 9개로 매우 적지만 spline 보간법을 활용하여 누락된 데이터를 보완하였다.
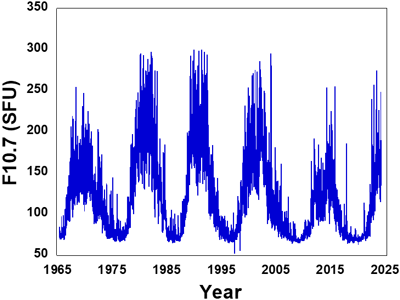
Fig. 3은 1965년부터 2023년까지 F10.7 지수의 일일 변화를 나타내고 있는데, 11년주기로 변화함을 알 수 있다. 태양활동 극대기에는 최고 300 Solar Flux Unit (SFU) 값을 가지며 극소기에는 최저 60 SFU 근처의 값을 가진다. 주기마다 극대값 수준은 약간씩 변화하는데, 2010년대의 극대값 수준은 1960 ~ 1990년대의 극대값 수준보다 약간 낮은 것을 알 수 있다. 1일 단위 데이터를 사용하였지만, 일일 측정 오차에 의한 영향을 감소시키기 위해서 5일 이동평균 데이터로 변환하여 사용하였다. 특정 날짜를 기준으로 4일전까지의 데이터를 평균하여 해당 날짜의 데이터로 사용하였다. 5일 평균을 사용한 이유는 GPS Klobuchar 모델에서 5일 이동평균 F10.7을 사용하여 전리층 모델 계수 예측을 수행하는 것으로 알려져 있기 때문이다 (Liu et al. 2024).
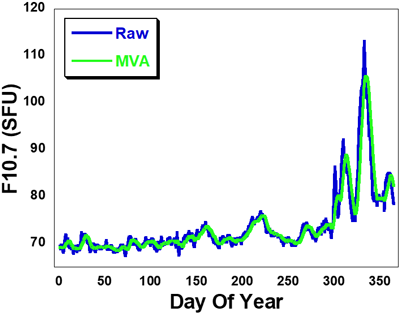
Fig. 4는 2020년 F10.7 일일 데이터와 5일 이동평균 데이터를 나타내고 있다. 2020년 후반기에는 태양활동 극대기로 진입하는 시기이기 때문에 F10.7이 증가하는 것을 알 수 있는데, 급격한 변화로 인해 시간지연 효과가 발생하는 것을 알 수 있다. 즉, 이동평균 시 원시 데이터와의 차이가 2020년 후반기에 급증하는데, 최대 14 SFU의 차이가 발생한다. 한편, LSTM 모델의 예측 알고리듬에 적용 시 이동평균 데이터를 평균이 0이고 표준편차가 1인 정규분포를 가지도록 정규화를 수행하였다.
F10.7 데이터의 예측 기간은 검증에 필요한 과거 데이터가 존재하는 2010년부터 2020년까지 총 11년으로 설정하였다. 예측 알고리듬의 학습에는 ARMA와 LSTM 모델을 사용하였으며, 두 모델의 학습 방식과 데이터 사용 기간에 차이가 있다. ARMA 모델의 경우, 계수
A
k
와
B
k
를 추정하기 위해 일반적으로 차수 합의 10배에 해당하는 데이터를 사용하였다. 너무 많은 데이터를 사용할 경우 과적합과 연산 시간 증가 문제가 발생할 수 있기 때문에, 최적화 과정을 통해 AR 차수
p
=
18
, MA 차수
q
=
9
로 설정하였다. 차수의 합인 27의 10배에 해당하는 270일의 데이터를 사용하여 ARMA 모델 계수를 추정한 후, 1일에서 7일 후의 데이터를 예측하였다. 예측 과정에서는 매일 과거 270일 데이터를 사용해 학습 (계수 추정)을 새로 수행하여 예측 성능을 높였다. 예를 들어, 2010년 1월 1일의 F10.7을 예측하기 위해 2009년 4월 6일부터 2009년 12월 31일까지의 데이터를 사용하며, 2010년 1월 2일의 예측에서는 2009년 4월 7일부터 2010년 1월 1일까지의 데이터를 새롭게 학습에 활용하였다. ARMA 차수를 결정하는 자세한 과정은 4.1절에서 설명한다.
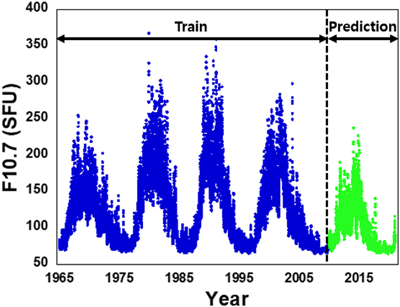
LSTM 모델은 가능한 많은 데이터를 사용하여 학습하는 것이 유리하다. 이에 따라 1965년부터 2009년까지 45년간의 데이터를 학습에 활용하였으며, 이는 약 4개의 태양 활동 주기에 해당하여 최근 태양 활동 변화 특성을 반영하기에 적합한 데이터이다. LSTM 모델은 이 45년 데이터를 이용해 학습한 뒤 네트워크를 생성하며, 이를 이용하여 1일 또는 7일 후의 F10.7 값을 예측한다. 이후 예측 과정에서는 예측된 데이터와 실제 관측 데이터를 결합하여 LSTM 모델을 매일 갱신함으로써 학습에 필요한 연산 시간을 최소화하였다. 예를 들어, 2일 후의 F10.7 값을 예측할 경우, 1일 후의 예측값을 포함한 데이터를 활용하여 LSTM 네트워크를 업데이트한다. Fig. 5는 LSTM 모델 학습에 사용된 데이터와 예측 및 검증에 사용된 데이터 구간을 나타내고 있다.
예측모델은 모델 파라미터 조합에 따라서 예측성능이 변화하므로 가능한 최적의 파라미터 조합을 찾기 위한 방법을 시도하였다. ARMA 모델의 최적화는 차수
p
와
q
에 의한 예측 기간에 따른 성능을 고려하였다. 매 예측 단계에서
p
+
q
의 10배에 해당하는 데이터를 사용하여 학습을 진행하였다. ARMA 모델의 학습 데이터는 최소 100개 이상 확보하는 것을 권장하기 때문이다 (Box & Jenkins 1970). ARMA 모델은 AR 모델의 차수
p
와 MA 모델의 차수
q
를 변경하면서 예측오차가 최소화되는 조합을 찾는 방법으로 최적화하였다.
p
는 1부터 25까지 변경하고,
q
는 1부터 9까지 변경하는 방법을 사용하였다. 예측성능을 판단하기 위한 지표로는 2.1절에서 설명한 AIC와 RMSE를 사용하였다. 연산시간을 단축하기 위하여 초기에는
p
와
q
의 변경간격을 6과 4로 크게 설정한 후, 최적해가 있는 영역에서 변경간격을 1로 단축하는 방법을 사용하였다.
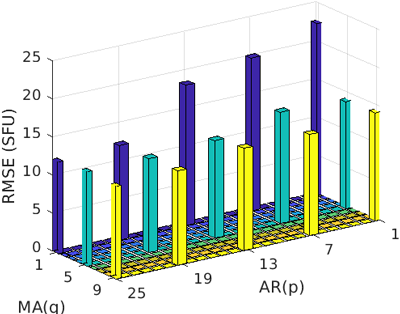
Fig. 6은 차수
p
와
q
의 변화에 따른 ARMA 모델 7일 예측 결과의 RMSE를 나타낸다. 최적화에 사용된 데이터 예측 기간은 2010년 1월부터 2020년 12월까지이며, 7일 이후의 값을 예측하였다. 그러나,
p
와
q
의 합이 커질수록 모델의 복잡성과 연산 시간이 증가하는 단점이 존재한다. 이를 고려하여, 차수 값을 보다 세밀하게 결정하기 위해 AIC를 추가로 활용하여 ARMA 모델의 차수를 최적화하였다.
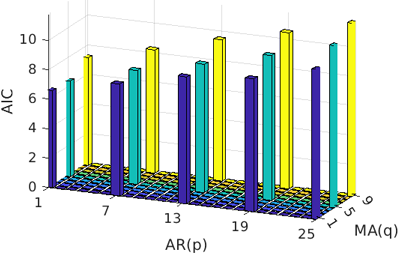
Fig. 7은 차수
p
와
q
의 변화에 따른 ARMA 모델 7일 예측 결과의 AIC를 보여준다. AIC는 차수의 합
p
+
q
가 계산에 반영되기 때문에, 같은 오차 수준에서 예측 모델의 복잡도가 높아질수록 학습에 소요되는 시간과, AIC 값이 증가한다. 이러한 특성으로 인하여,
p
=
1
,
q
=
1
일 때 AIC 값이 가장 작게 나타나며, 이는 차수 변화에 따른 시스템 복잡도 변화에 비해 오차의 변화가 작음을 의미한다. 높은 차수에서의 AIC 오차를 분석한 결과,
p
가 7에서 19 사이일 때 오차가 근소하게 감소하는 경향을 보였다. 이를 바탕으로
p
를 8부터 18까지 1 단위로 변경하며 RMS 오차와 AIC 변화를 관찰하였다. 이러한 최적화 과정을 통해 ARMA 모델의 최적 차수를
p
=
18
,
q
=
9
로 결정하였다.
예측기간에 따라 ARMA 최적 파라미터 구성이 차이가 나기 때문에 1일 예측기간에 대한 파라미터 최적화도 수행하였다. 1일 예측오차는 7일 예측오차와 유사하게
p
와
q
차수가 증가할수록 RMSE는 감소하지만, AIC는 증가하는 경향을 나타내었다. 1 일 예측인 경우
p
,
q
차수 변화에 따른 RMSE 변화폭이 0.9 SFU에 불과하여, 변화폭이 10 SFU인 7일 예측에 비해 최적화 효과가 매우 작았다. 이러한 이유로 7일 예측에 최적화된 파라미터를 1일부터 6일 예측에도 적용하였다.
본 연구에서는 LSTM 모델에 Bayesian 기법을 적용하여 최적화를 수행하였다. LSTM 모델의 최적화는 다양한 hyper parameter와 이들의 조합을 고려해야 하는 복잡한 과정으로, 이를 적절히 수행하기 위해 세부적인 조정이 필요하다. LSTM 모델에서 최적화 대상이 되는 주요 hyper parameter로는 LSTM 계층 수, 각 LSTM 계층의 은닉층 노드 수, 최적화 기법 (optimizer), 에포크 (epoch), 미니배치 크기 (minibatch size), 학습률 (learning rate), 학습률 감소 기간 (learning rate drop period), 학습률 감소율 (learning rate drop factor) 등이 있다. 이러한 hyper parameter들은 방대한 수의 조합을 형성하며, 경우의 수가 매우 많기 때문에 이를 모두 탐색하는 데에는 과도한 시간이 소요된다. 기존에 널리 사용되는 random search 기법은 일부 조합만을 임의로 실험하기 때문에 최적화 정확도가 떨어질 가능성이 있으며, 도출된 결과가 전역 최적해임을 보장하지 못한다는 단점이 있다. 또다른 최적화 기법인 grid search 기법은 모든 hyper parameter의 조합을 고려하여 최적해를 찾아내는 방법이기 때문에 연산 비용이 천문학적으로 증가한다는 단점이 존재한다. 이러한 문제를 해결하기 위한 효율적인 접근법으로 Bayesian 최적화 기법을 선택하였다.
고려해야 할 hyper parameter의 개수가 많기 때문에 최적화를 위한 반복 계산 시 많은 연산 시간이 소요되므로 2010년부터 2020까지 11년 데이터를 이용하여 학습을 수행한 뒤, 7일 후의 F10.7 예측을 수행한 후 실제 F10.7과의 비교로부터 예측 오차를 산출하였다. 2단계로 나누어서 최적화를 수행하였는데, 1단계에서는 은닉층 노드 수를 제외한 파라미터를 최적화하기 위하여 각종 파라미터를 변경시켜 가면서 170회의 탐색을 수행하였다. 이 과정에서 각 파라미터들의 초기 탐색 범위를 설정한 뒤, 반복적으로 Bayesian 최적화를 적용하였다. 2단계에서는 1단계 결과를 기반으로, 은닉 노드 수를 최적화하기 위하여 2개의 LSTM 계층을 대상으로 추가 탐색을 수행하였다.
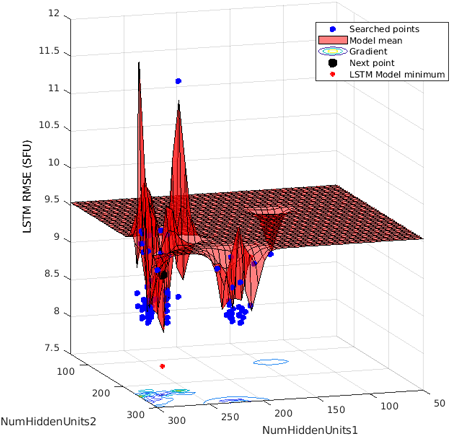
Fig. 8은 Bayesian 최적화 기법을 사용하는 과정을 나타내고 있는데, 2개 은닉층 수에 따른 예측오차 RMS의 변화를 나타내고 있다. 하단의 빨간색 점은 최적 은닉층 조합일 때의 오차 RMS를 나타낸다. Table 1은 LSTM 파라미터의 최적화 결과를 나타내고 있다. 네트워크는 총 6개의 층으로 구성되어 있으며, 시계열 데이터를 입력으로 받아 완전 연결 계층을 거쳐 두 개의 LSTM 층을 지난다. 은닉층의 개수는 각각 274, 250이며, LSTM 계층을 지날 때마다 활성화 함수로 정류된 선형 함수 (Rectified Linear Unit, ReLU)를 사용하였을 경우 가장 성능이 좋았다.
table
1965년 1월 1일부터 2009년 12월 31일까지의 F10.7 관측 데이터를 사용하여 2010년 1월 1일부터 2020년 12월 31일까지 총 11년간의 F10.7 값을 예측하였다. ARMA와 LSTM 모델을 사용하여 1일부터 7일 후의 값을 추정했으며, 성능 비교를 위해 구현이 간단한 다항식 기반의 예측도 수행하였다. 과거 데이터를 이용한 내삽 (interpolation)으로 다항식 계수를 결정한 후, 이를 외삽 (extrapolation)하여 예측하였고, 다항식의 차수를 1차부터 4차까지 변경하며 RMS 오차를 계산한 결과, 2차 다항식에서 RMS 오차가 최소값을 나타냈다. 따라서 2차 다항식을 이용한 예측 결과를 ARMA 및 LSTM 모델 결과와 비교하였다.
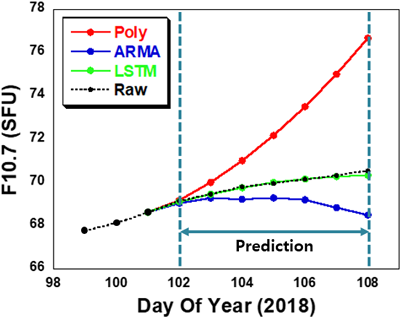
Fig. 9는 2018년 4월 12일 (DOY 102)부터 18일 (DOY 108)까지 7일간의 F10.7 예측 결과를 보여준다. 다항식 모델은 2차 다항식을 사용하였으며, 4월 9일부터 11일까지 3일간의 데이터를 활용해 2차 다항식 계수를 결정하였다. ARMA 모델은 4월 11일까지의 과거 270일 데이터를 이용해 학습을 진행하였고, LSTM 모델은 2009년까지 학습하여 네트워크를 생성한 뒤 2018년 4월 11일까지의 실제 F10.7 데이터를 반영하여 네트워크를 갱신하였다. 다항식 모델은 예측 기간이 길어질수록 실제 F10.7 데이터 (raw)와의 차이가 급격히 증가하며, F10.7 예측에 적합하지 않은 모델임을 확인할 수 있다. ARMA 모델은 1일 또는 2일 정도까지는 실제값에 근접한 예측값을 생성하지만, 예측 기간이 길어질수록 오차가 증가하는 경향을 보였다. 반면, LSTM 모델은 7일 후까지도 실제값과 거의 유사한 예측값을 생성하며 안정적인 성능을 보였다.
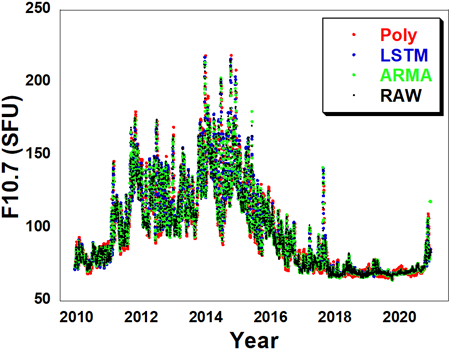
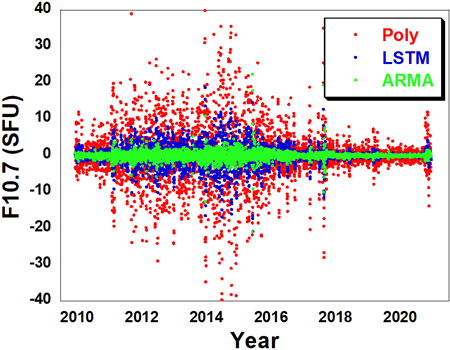
Fig. 10은 2010년부터 2020년까지 11년 동안 ARMA와 LSTM 모델을 이용하여 1일 후 F10.7 데이터를 예측한 결과를 나타내고 있다. 2014년에 태양활동 극대기를 지난 후에 F10.7의 세기가 약해지다가 2020년 후반에 점차 증가하는 것을 알 수 있다. 2017년은 극소기에 진입하는 시기이지만 일시적으로 F10.7이 반등한 것을 알 수 있다. 실제 (raw) 데이터와 비교하면 ARMA와 LSTM 모델의 예측결과는 거의 유사한 값을 나타내지만, 다항식 예측결과는 어느 정도의 차이를 나타낸다. Fig. 11은 2010년부터 2020년까지 11년 동안 1일 후 F10.7 예측데이터의 오차를 비교하고 있다. 태양활동 극대기에 오차 크기가 증가하는 경향을 보이며 다항식 모델로 예측 시 최대 오차는 50 SFU이다. ARMA와 LSTM 모델의 오차 수준은 큰 차이가 없다.
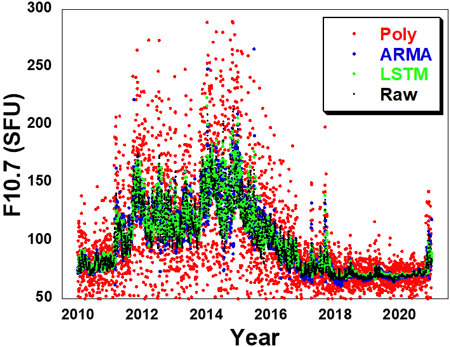
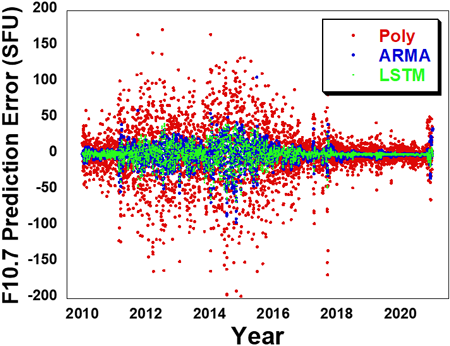
Fig. 12는 2010년부터 2020년까지 11년 동안 7일 후 F10.7 데이터를 예측한 결과를 나타내고 있다. 1일 예측 결과인 Fig. 10에 비해 다항식 예측값의 분산이 증가하여 실제 (raw) 값과의 차이가 상당히 발생함을 알 수 있다. 특히 태양활동 극대기인 2012년에서 2015년 사이에 차이가 급증하는데, 이로부터 다항식 모델은 7일 후 예측에는 부적합한 것을 알 수 있다. ARMA 모델은 LSTM 모델과 유사하지만 부분적으로 분산정도가 증가하는 것을 알 수 있다. Fig. 13은 2010년부터 2020년까지 11년 동안 7일 후 F10.7 예측데이터의 오차를 비교하고 있다. 태양활동 극대기인 2012년에서 2015년 사이에 예측오차가 급증하며, 태양활동 극대기에 진입하는 2020년 후반에 다시 급등하는 것을 알 수 있다. ARMA 모델이 LSTM 모델에 비해 좀 더 높은 수준의 예측오차를 나타내고 있다.
테이블
Table 2는 2010년부터 2020년까지 11년 동안 1일 후와 7일 후 F10.7 예측데이터의 오차의 통계값을 비교하고 있다. 실제 F10.7 값 대비 오차 비율도 같이 제시하였다. 모든 예측 오차의 평균은 0에 근접하는데, 이는 예측모델의 오차 편이가 낮은 수준임을 의미한다. 이러한 이유로 오차 RMS의 대부분 성분은 오차의 표준편차 성분으로 구성된다. 1일 예측오차 RMS에 비해 7일 예측오차 RMS는 3.1배 (LSTM)에서 9.9배 (ARMA)까지 증가하는데, LSTM 모델에 비해 ARMA 모델의 오차 증가폭이 높다. 이는 중장기 예측 시 ARMA 모델보다 LSTM 모델이 유리하다는 것을 의미한다. ARMA 모델의 1일 예측오차 비율은 0.9%로 F10.7 관측값에 근접하는 매우 낮은 수준을 나타내고 있다. F10.7 예측데이터를 입력값으로 사용하는 GPS Klobuchar 모델의 경우 전리층 지연값 오차는 50% 수준으로 알려져 있는데, 이를 고려하면 0.9% 수준의 입력값 오차는 전리층 보정정보 예측값 생성에 사용할 수 있는 수준으로 생각된다. LSTM 모델의 7일 예측오차 비율은 7.1% 로 1일 예측오차에 비해 증가하였지만, 이 역시 전리층 보정정보 예측값 생성에 사용할 수 있는 수준으로 생각된다.
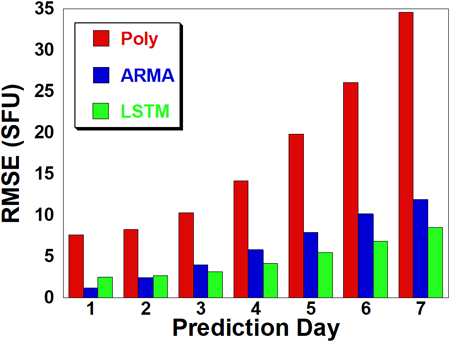
Fig. 14는 11년간의 예측 결과에서 7일간 일별 오차의 전체적인 변화에 대하여 설명한다. 그래프를 보면, 예측 3일차부터 LSTM 모델의 오차가 ARMA 오차보다 근소한 차이로 낮아지는 경향을 확인할 수 있다. 이는 두 모델의 예측 기법 차이에서 기인한 결과로 분석할 수 있다. ARMA 모델은 최신 과거 데이터들의 선형 결합을 기반으로 예측을 수행하기 때문에, 1, 2일차 예측과 같이 예측 일수가 매우 짧을 경우 LSTM 모델보다 더 좋은 성능을 보이지만, 예측 일수가 길어질수록 ARMA 모델의 선형적인 접근 방식은 데이터의 장기적인 비선형적 패턴과 변동성을 충분히 반영하기 못하기 때문에 예측의 불확실성이 더 크게 나타난다. 반면, LSTM 모델은 시간에 따른 데이터의 패턴을 더 잘 학습하고, 장기 종속성을 학습하는 데 유리하다. 이로 인하여 초기 예측 기간에서는 ARMA 모델보다 성능이 다소 떨어질 수 있지만, 예측 기간이 길어질수록 데이터의 변화를 효과적으로 반영하여 안정적인 성능을 보이는 것으로 해석할 수 있다.
본 연구와 유사한 기존 논문결과와 비교하면, 7일 이내의 예측정확도는 본 연구가 우수한 것으로 파악된다. AR 모델을 사용한 Du (2020) 연구의 경우 7일 예측오차 평균은 10.4 SFU이며, 역시 AR 모델을 사용한 Liu et al. (2010) 연구의 경우 1일 예측오차 평균이 2.0%로 본 연구 결과보다 오차수준이 다소 높은 것으로 파악된다. LSTM을 사용한 Zhang et al. (2022) 연구의 경우에도 1일 예측오차 평균은 6.4 SFU로 본 연구 결과보다 오차수준이 높은 것으로 파악된다. 예측오차 수준은 예측기법 뿐만 아니라 최적화정도에 따라 많이 달라지게 되는데, 본 논문은 7일 이내 예측정확도 최적화에 주안점을 두었으므로, 중장기 예측을 주로 다루는 기존 논문보다 우수한 성능을 나타내었다고 할 수 있다. 기존 논문결과에는 최적화결과가 상세히 기술되지 않은 경우도 있으므로 단기예측에 대한 본 연구의 최적화결과는 유용하게 활용될 수 있다.
GNSS 신호 오차의 주요 성분인 전리층에 의한 신호지연은 태양활동과 밀접한 관련이 있으며, GPS Klobuchar 등과 같은 전리층 보정정보 예측모델은 태양활동 지수인 F10.7 예측값을 입력값으로 사용하는 것으로 알려져 있다. 이러한 이유로 F10.7 예측정확도를 높이는 것은 GNSS 신호지연 오차를 줄이는데 매우 중요하다. 본 연구에서는 시계열데이터 예측에 많이 사용되는 ARMA 모델과 LSTM 모델을 이용하여 F10.7을 예측하는 알고리듬을 개발하였다. 45년간 F10.7 데이터를 사용하여 학습을 진행한 뒤, 11년간 예측성능을 분석하였고, 예측기간은 1일부터 7일로 설정하였다.
예측모델의 최적화를 위해 ARMA 모델 차수 변경 및 LSTM-Bayesian 방법을 사용하여 모델 파라미터를 결정하였다. 비교를 위해 다항식을 이용한 예측도 수행하였는데, 예측오차 수준이 높아서 적용하기에는 부적합한 것으로 파악되었다. 1일 예측오차의 경우 실제 F10.7 값 대비 ARMA 모델은 0.9%, LSTM 모델은 2.1%로 매우 낮은 수준을 나타내었다. 또한 7일 오차의 경우 ARMA 모델은 10.5%, LSTM 모델은 7.1%로 1일 오차수준보다는 증가했지만 폭이 크지는 않았다. 예측기간이 증가할수록 ARMA 모델에 비해 LSTM 모델의 오차수준이 낮게 유지되지만, 1일 예측의 경우 ARMA 모델도 충분한 성능을 산출하는 것으로 생각된다. ARMA 모델이 LSTM 모델에 비해 알고리듬 구현 난이도가 낮고, 최적화 파라미터 변화에 의한 불안정성이 낮으므로 단기 예측에는 충분히 활용될 수 있을 것으로 보인다. 두 방법 모두 전리층 보정정보 예측값 생성에 충분히 활용될 수준인 것으로 파악된다. 최근에는 LSTM을 확장한 CNN-LSTM 또는 VMD-LSTM을 이용한 F10.7 예측에 관한 연구가 시도되고 있는데, 향후 이러한 기법을 적용하여 예측 정확도 및 신뢰성을 높이는 연구가 필요하다.
None.
Conceptualization, J.K.; formal analysis, S.Y. and Y.K.; data curation, S.Y. and Y.K.; writing—original draft preparation, S.Y. and Y.K.; writing—review and editing, J.K.; project administration, J.K.; funding acquisition, J.K.
The authors declare no conflict of interest.
Abdel-Rahman, H. I. & Marzouk, B. A. 2018, Statistical method to predict the sunspots number, NRIAG Journal of Astronomy and Geophysics, 7, 175-179. https://doi. org/10.1016/j.nrjag.2018.08.001
Akaike, H. 1974, A new look at the statistical model identification, IEEE Transactions on Automatic Control, 19, 716-723. https://doi.org/10.1109/TAC.1974.1100705
Box, G. E. P. & Jenkins, G. M. 1970, Time Series Analysis: Forecasting and Control (San Francisco: Holden-Day).
Chatterjee, T. N. 2001, On the application of information theory to the optimum state-space reconstruction of the short-term solar radio flux (10.7 cm), and its prediction via a neural network, Monthly Notices of the Royal Astronomical Society, 323, 101-108. https://doi. org/10.1046/j.1365-8711.2001.04110.x
Cui, Z., Ke, R., Pu, Z., & Wang, Y. 2018, Deep Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction, in International Workshop on Urban Computing (UrbComp), Nova Scotia, Canada, 14 Aug. 2017.
Du, Z. 2020, Forecasting the Daily 10.7 cm Solar Radio Flux Using an Autoregressive Model, Solar Physics, 295, E125. https://doi.org/10.1007/s11207-020-01689-x
GFZ, Helmholtz Centre for Geosciences [Internet], cited 2024 Jul 28, available from: https://kp.gfz-potsdam.de/ en/data
Hao, Y., Lu, J., Peng, G., Wang, M., Li, J., et al. 2024, F10.7 Daily Forecast Using LSTM Combined with VMD Method, Space Weather, 22, 1-13. https://doi. org/10.1029/2023SW003552
Hochreiter, S. & Schmidhuber, J. 1997, Long Short-Term Memory, Neural Computation, 9, 1735-1780. https:// doi.org/10.1162/neco.1997.9.8.1735
Huang, C., Liu, D.-D., & Wang, J.-S. 2009, Forecast daily indices of solar activity, F10.7, using support vector regression method, Research in Astronomy and Astrophysics, 9, 694-702. https://doi.org/10.1088/16744527/9/6/008
Hyndman, R. J. & Athanasopoulos, G. 2021, Forecasting: Principles and Practice, 3rd ed. (Melbourne, Australia: OTexts).
Iqbal, M. F., Zahid, M., Habib, D., & John, L. K. 2019, Efficient Prediction of Network Traffic for Real-Time Applications, Journal of Computer Networks and Communications, 2019, Article ID 4067135. https://doi. org/10.1155/2019/4067135
Kim, B. & Kim, J. 2022, Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change, Sensors, 22, E9421. https://doi.org/10.3390/ s22239421
Kim, B. C., Kim, Y. G., & Lee, S. H. 2020, A Prediction of Solar Activity Indicator F10.7 using LSTM Network, Journal of the Korean Data Analysis Society, 22, 169-176. https:// doi.org/10.37727/jkdas.2020.22.1.169
Kim, J. & Kim, Y. 2023, Long-term Analysis of Availability and Accuracy Variation of GPS Ionospheric Delay Model, Journal of Advanced Navigation Technology, 27, 841-848. https://doi.org/10.12673/jant.2023.27.6.841
Klobuchar, J. A. 1987, Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users, IEEE Transactions on Aerospace and Electronic Systems, AES-23, 325-331. https://doi.org/10.1109/TAES.1987.310829
Liu, S., Zhong, Q., Wen, J., & Dou, X. 2010, Modeling Research of the 27-day Forecast of 10.7 cm Solar Radio Flux (I), Chinese Astronomy and Astrophysics, 34, 305315. https://doi.org/10.1016/j.chinastron.2010.07.006
Liu, Z., Fang, R., Hu, Z., Zhang, Q., Liu, X., et al. 2024, A revised BDS Klobuchar model with a non-symmetrical processing strategy and a high-latitude amplitude constraint, Advances in Space Research, 73, 780-793. https://doi.org/10.1016/j.asr.2023.10.026
Luo, J., Zhu, L., Zhang, K., Zhao, C., & Liu, Z. 2022, Forecasting the 10.7-cm Solar Radio Flux Using Deep CNN-LSTM Neural Networks, Processes, 10, E262. https://doi.org/10.3390/pr10020262
NOAA, Space Weather Prediction Center [Internet], cited 2024a July 26, available from: https://www.swpc.noaa. gov/impacts/space-weather-and-gps-systems
NOAA, Space Weather Prediction Center [Internet], cited 2024b July 26, available from: https://www.swpc.noaa. gov/phenomena/f107-cm-radio-emissions
NOAA, Space Weather Prediction Center [Internet], cited 2024c July 26, available from: https://www.swpc.noaa. gov/phenomena/total-electron-content
Snoek, J., Larochelle, H., & Adams, R. P. 2012, Practical Bayesian Optimization of Machine Learning Algorithms, Advanced in Neural Information Processing Systems, 4. https://doi.org/10.48550/arXiv.1206.2944
Tapping, K. F. 2013, The 10.7 cm solar radio flux (F10.7), AGU Space Weather, 11, 394-406. https://doi.org/10.1002/ swe.20064
Wen, J., Zhong, Q., & Liu, S. 2010, Model Research of 10.7 cm Solar Radio Flux 27-day Forecast, Chinese Journal of Space Science, 30, 198-204. https://doi.org/10.11728/ cjss2010.03.198
Yule, G. U. 1927, On a Method of Investigating Periodicities Disturbed Series, with Special Reference to Wolfer’s Sunspot Numbers, Philosophical Transactions of the Royal Society of London, 226, 267-298. https://doi. org/10.1098/rsta.1927.0007
Zhang, W., Zhao, X., Feng, X., Liu, C., Xiang, N., et al. 2022, Predicting the Daily 10.7-cm Solar Radio Flux Using the Long Short-Term Memory Method, Universe, 8, E30. https://doi.org/10.3390/universe8010030