Ei-Ju Sim1, Kwan-Dong Park1,2†
1Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
2PP-Solution Inc., Seoul 08504, Korea
†Corresponding Author: Kwan-Dong Park, E-mail: kdpark@inha.ac.kr
Citation: Sim, E.-J. & Park, K.-D. 2025, Simultaneous Estimation of the Night Delay Constant and Coefficients of a Regional Klobuchar Model Using IGS GIM, Journal of Positioning, Navigation, and Timing, 14, 29-35.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 March, Volume 14, Issue 1, pages 29-35. https://doi.org/10.11003/JPNT.2025.14.1.29
Received on Jan 22, 2025, Revised on Feb 05, 2025, Accepted on Feb 12, 2025, Published on Mar 15, 2025.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In Global Navigation Satellite System (GNSS) signal transmission, the ionosphere is the most significant source of error. The Klobuchar model, a widely used ionospheric error correction model, relies on correction coefficients transmitted in Global Positioning System (GPS) navigation messages to provide global coverage. However, its accuracy is limited to approximately 50–60%. In this study, correction coefficients and Delay Constant (DC) values were estimated using International GNSS Service (IGS) Global Ionospheric Map (GIM) data to enhance the accuracy of the regional Klobuchar model, and the resulting improvements were analyzed. The grid point range for estimating the correction coefficients was defined as latitude 22.5–50° and longitude 105–150°, considering the Ionosphere Pierce Point (IPP) range over the Korean Peninsula. After calculating the Vertical Total Electron Content (VTEC) for each model, correction coefficients and DC values were simultaneously estimated using the least squares method. To evaluate the performance, the DC values were analyzed over periods with varying solar activity, and accuracy was validated based on VTEC Root Mean Square Error (RMSE) and positioning accuracy using IGS GIM as a reference. When DC values were estimated simultaneously, the VTEC RMSE improved by 54.8–74.4% compared to the original Klobuchar model, regardless of the solar activity intensity. Furthermore, positioning results at the Daejeon Station indicated horizontal accuracy improvements of approximately 1.7–40.0% and vertical accuracy improvements of approximately 34.8–37.4%.
GNSS, ionosphere, Klobuchar model coefficients, night delay constant, IGS GIM
Global Navigation Satellite System (GNSS) 측위 오차의 종류는 위성과 수신기, 그리고 전달 경로에 의한 오차로 나눌 수 있다. 그 중에서도 전리층에 의한 오차는 가장 큰 오차 요인으로 작용하고 있다 (Misra & Enge 2006). 이러한 전리층 오차를 보정하기 위해 다양한 방법들이 사용되고 있으며, 이중 주파수 수신기 사용자의 경우에는 두개의 주파수를 조합하는 무전리층 조합을 통해 전리층 오차를 제거할 수 있다. 하지만 이중주파수 수신기는 높은 가격으로 인해 대중화 속도가 느리기 때문에 저가의 단일주파수 수신기가 널리 사용되고 있다. 단일주파수 수신기의 경우 무전리층 조합을 사용할 수 없으므로 전리층 오차 보정을 위해 Global Ionospheric Map (GIM)과 Klobuchar 모델을 사용한다.
GIM은 전세계 상시관측소에서 수집된 데이터를 처리해 생성한 전지구 격자형 전리층 지도이다. GIM은 전지구를 위도 2.5°, 경도 5° 간격의 격자로 나눠, 각 격자점에서 2시간 간격으로 계산된 수직방향 총전자수(Vertical Total Electron Content, VTEC) 데이터를 하루 단위로 제공한다. 다수의 International GNSS Service (IGS) 분석센터는 신속산출물(rapid product)과 최종산출물(final product)을 공통으로 제공하며, 일부 분석센터에서는 1-2일 전에 생성되는 예측산출물(predicted product)을 제공하기도 한다 (IGS 2025). 예측산출물은 실시간 사용이 가능하다는 이점이 존재하지만 최종산출물과 비교할 경우 정확도가 다소 낮다. 반면 최종산출물은 2~8 Total Electron Content Unit (TECU)의 정확도로 우수한 보정성능을 보이지만 후처리 모델로 실시간 사용이 불가능하다는 단점이 있다.
Klobuchar 모델로 위성과 수신기 사이의 전리층 지연량을 계산할 수 있다. 전리층 지연량을 산출하기 위해서는 Global Positioning System (GPS) 항법메시지에 송출되는 보정계수인
α
n
,
β
n
(
n
=0~3)을 이용한다. 주간 시간 동안의 전리층 지연량은 사용자의 위치, 보정계수, 시각을 이용하여 계산하는 반면, 야간 시간의 전리층 지연량은 야간지연상수(Delay Constant, DC)인 5 ns로 고정한다. Klobuchar 모델은 전리층 오차를 50~60%의 수준으로 보정하지만, 실시간 사용이 가능하다는 이점과 모델의 계산 단순성으로 인해 널리 사용되고 있다 (Klobuchar 1987).
Klobuchar 모델의 보정계수는 사용자의 위치, 시각과 무관하게 전지구를 대상으로 하루에 한 세트씩 송출되고 있다. 전리층은 위도에 따라 특성이 다르기 때문에, 다른 위도대에 위치한 사용자가 동일한 보정계수를 사용한다면 정확도가 낮아질 것으로 판단된다. 또한 사용자의 위치적 특성을 고려하지 않고 전지구적으로 동일한 야간지연상수를 사용하는 것은 Klobuchar 모델의 보정 성능 저하에 영향을 미칠 것으로 보인다.
이러한 Klobuchar 모델의 한계점을 극복하기 위해, 보정계수를 추정하는 다양한 선행 연구가 수행되었다. Zhang et al. (2022)은 Klobuchar 모델의 정확도를 높이기 위해
α
n
(
n
=0~3),
β
n
(
n
=0~2) 그리고 야간지연상수를 파라미터로 도입하여 총 8개의 매개변수를 추정하였다. 수정된 보정계수는 북반구에서 기존 모델 대비 47%의 성능 향상을 나타냈다. Wang et al. (2019)은 전리층 오차를 줄이기 위해 Klobuchar 모델을 개선한 Nklob 모델을 제안하였다. 시간, 지자기 위도, 전리층의 주기적인 변동을 반영한 경험적 야간 지연 모델을 사용해 기존 모델 대비 보정 성능을 6% 개선하였다. Nishimoto et al. (2013)은 Klobuchar 모델의 보정계수를 Spherical Cap Harmonics Analysis (SCHA) 모델을 이용하여 개선하였다. 보정계수
α
n
,
β
n
을 추정하기 위해 최소제곱법을 이용하였으며, DC 값은 SCHA 모델의 평균값으로 대체하였다. 일본 내 3개 관측소에서 실험한 결과, 수직 방향에서 평균 74.8%, 수평 방향에서 기존 Klobuchar 모델 대비 평균 62.5%의 개선 효과를 보였다. 또한 Klobuchar 모델의 야간지연상수를 개선하기 위해 Zhou et al. (2018)는 야간지연상수를 적용할 적합한 시간대를 비교하였으며 지방시 기준 20:00~06:00가 가장 적합한 시간대라는 결과를 도출하였다. 그리고 위도별 야간 시간 동안의 Nighttime VTEC (NVTEC) 변동성과 계절별 NVTEC 평균을 고려한다면 Klobuchar 모델의 기존 야간지연상수인 5 ns는 부적합하다는 결론을 도출하였다. 선행연구를 살펴보면 전지구를 대상으로 수행된 결과이기 때문에 국지적인 지역에 적용이 어려우며 사용자의 위치가 변화할 경우에도 한계가 있다.
이 연구에서는 지역적 Klobuchar 모델의 정확도를 높이기 위해 최소제곱법을 이용해 보정계수와 DC를 동시에 추정하였으며 IGS GIM과 비교하여 정확도를 검증하였다. 먼저 전리층 오차 보정 모델에 대해 설명하고, 보정계수를 추정하기 위한 절차를 3단계로 세분화하였다. 지역적 특성만을 고려하기 위해 사용 격자점의 범위를 한반도의 Ionosphere Pierce Point (IPP)를 고려한 위도 22.5~50°, 경도 105~150°로 설정하였다. 다음으로, 모델별로 설정 격자점에서의 VTEC을 산출하였다. 보정계수와 DC는 최소제곱법을 이용해 추정하였다. 태양활동에 따라 추정한 DC를 기존 DC와 비교하였으며 IGS GIM을 기준으로 전체 격자점에서의 VTEC Root Mean Square Error (RMSE)를 산출해 정확도를 확인하였다. 마지막으로 추정된 보정계수와 DC의 성능 검증을 위해 대전관측소에서의 측위정확도를 산출한 후 정확도를 평가하였다.
GIM은 자유전자가 약 450 km 상공의 단일층에 집중되어 있다고 가정한 모델로, 전지구 격자점에서의 VTEC을 TECU 단위로 제공한다. GIM은 IONosphere Map Exchange (IONEX) 데이터 형식으로 제공되며 위도 2.5°, 경도 5°의 공간 해상도와 2시간의 시간해상도를 가진다. 사용자가 GIM을 활용하여 전리층 지연량을 계산하기 위해서는 사용자와 관측 위성 간의 시선 벡터와 단일층으로 가정된 전리층과 교차하는 IPP를 산출해야 한다. IPP와 인접한 4개의 격자점을 선택하고 사용자의 위치와 시간을 고려해 시공간 보간을 한다. 보간된 VTEC에 전리층 사상 함수를 적용하면 시선 방향에 대한 전리층 지연량을 산출할 수 있다. 보간법과 관련된 내용은 Schaer et al. (1998)에 자세히 소개되어 있다.
Klobuchar 모델은 계산 단순성으로 인해 가장 널리 사용되는 전리층 오차 보정 모델이다. Klobuchar 모델은 전리층을 350 km 상공에 자유전자가 밀집된 단일층으로 가정하며 사용자와 위성 간 시선 벡터를 따라 전리층 지연량을 계산한다. Klobuchar 모델로 전리층 지연량을 구하기 위해서는 사용자의 위치, 위성의 3차원 좌표, 관측 시각 그리고 보정계수인
α
n
,
β
n
이 필요하다. Klobuchar 모델은 전리층 지연량을 야간과 주간으로 구분하여 보정한다. 야간에는 전리층 지연량을 야간지연상수인 5 ns로 고정하며, 주간에는 14시에 위상이 최대인 half-cosine 함수로 가정한다. 이때 half-cosine 함수의 진폭인 AMP와 주기인 PER은 항법메시지에 송출되는 보정계수를 이용하여 계산하며 Eqs. (1, 2)를 통해 계산한다. 여기서
ϕ
n
m
는 지자기 위도이다.
수식
최종적으로 전리층 지연량을 구하는 식은 Eq. (3)과 같다. Eq. (3)의 F는 수직방향 전리층 지연량을 시선방향 전리층으로 변환해주는 Slant Factor이며, Eq. (4)의
X
I
는 코사인 함수의 라디안을 나타낸다. Klobuchar 모델로 전리층 지연량을 구하는 전체 과정은 Klobuchar (1987)에 자세히 소개되어 있다.
수식
지역적 Klobuchar 모델의 정확도를 높이기 위해서는 GIM의 모든 격자점을 사용할 필요가 없다. 사용자의 위치를 고려하여 격자점의 범위를 한정할 수 있기 때문에 이 연구에서는 사용자가 한반도에 위치한다고 가정하여 한반도 인근 격자점을 선택하였다. 격자점의 범위를 설정하기 위해 한반도 내 6개 지점을 선정한 후, 모든 지점에서 24시간 동안의 IPP를 산출하였다. IPP 산출을 위한 임계고도각은 15°로 가정하였다. 각 지점의 지리적 위치는 Fig. 1a에, 모든 지점에서 발생한 IPP는 Fig. 1b에 나타냈다. 이를 고려하여 Sim et al. (2023)의 격자 범위와 동일하게 격자점의 범위를 위도 22.5~50°, 경도 105~150°로 설정하였다. GIM의 공간해상도를 고려한다면 격자점의 개수는 위도 방향으로 12개, 경도 방향으로 10개씩 존재하므로 총 120개가 된다.
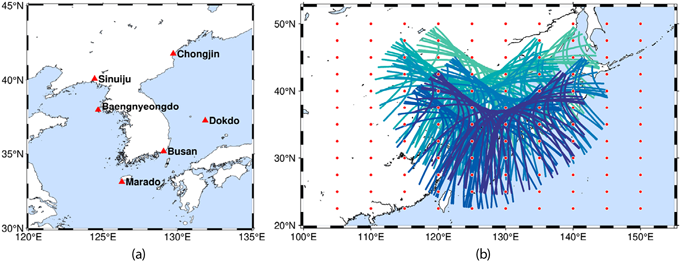
Klobuchar 모델의 보정계수와 DC를 추정하기 위해서는 설정 격자범위에서 모델별 VTEC을 구해야 한다. 이를 위해 모든 격자점에 관측소가 위치한다고 가정하였다. GIM은 각 격자점에서의 VTEC을 제공하므로 그대로 사용하였다. 다음으로 Klobuchar 모델로 VTEC을 구하기 위해 모든 격자점의 상공에 위성이 존재한다고 가정하였다. 이러한 가정을 할 경우 위성의 고도각과 방위각은 각각 90°, 0°로 설정된다. Eq. (5)의 E는 위성의 고도각을 나타내며 Klobuchar 모델식에서의 모든 단위는 semi-circle로 계산되기 때문에 E는 0.5다. 따라서 위성의 고도각이 90°라면 Eq. (5)에 의해 VTEC을 STEC으로 변환해 주는 F는 1로 가정할 수 있다.
수식
모델별로 VTEC을 구할 때의 시간 간격은 GIM의 시간 해상도와 동일한 2시간으로 설정했다. 이는 별도의 시간 보간을 필요로 하지 않는다는 장점이 있다. 또한 위성이 각 격자점의 상공에 위치한다고 가정하므로 위성 궤도력 파일이 필요 없고, 위성 위치 계산 과정을 생략할 수 있어 효율성이 향상된다는 장점이 있다.
이 연구에서는 최소제곱법을 이용하여 보정계수와 DC를 동시에 추정하기 위해, Eq. (3)의 상수인 DC를 미지수로 가정하였다. 보정계수 추정을 위해 조성한 설계행렬이며 총 9개의 미지수를 추정하기 때문에 9개의 열로 구성된다. 보정계수를 추정하는 자세한 과정은 Park et al. (2025) 논문으로 대체한다. 앞으로 이 연구에서 추정한 보정계수와 DC는 NEW로, 기존 보정계수는 Legacy (LEG)로 칭하기로 한다.
보정계수와 DC 추정을 위한 분석 기간을 선택하기 위해 태양활동의 영향을 받는 전리층의 특성을 고려하였다. GPS는 태양활동 수준을 10단계로 구분한 뒤, 태양 플럭스 수치의 5일 이동 평균값에 따라 370개의 상수 세트 중 LEG를 선택한다 (Yuan et al. 2008). 따라서 이 연구에서는 태양활동을 고려하기 위해 Fig. 2에 태양활동지수인 F10.7의 11년간의 연평균 값을 나타냈다. 2013년부터 2023년 중 연평균 F10.7이 가장 낮았던 2019년과 가장 높았던 2023년을 분석기간으로 설정하였다.
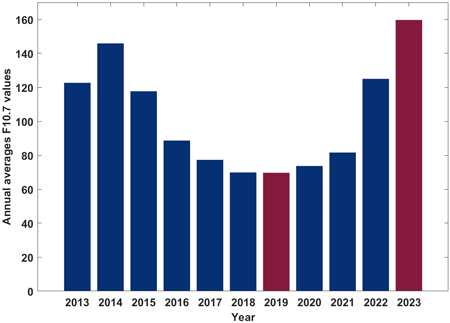
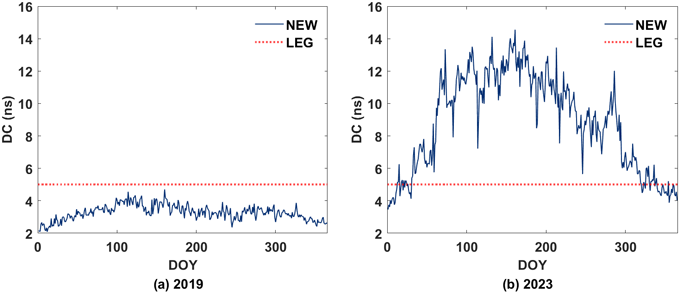
Fig. 3에는 2019년과 2023년의 일별 DC 추정값을 나타냈다. 빨간색 점선은 LEG DC를, 남색 실선은 NEW DC를 나타낸다. 태양활동이 평이했던 2019년의 경우 모든 일자에서 5.0 ns 이하로 추정되었다. 2019년의 연평균 DC 값은 3.27 ns로 LEG DC보다 1.73 ns 낮았으며, 표준편차는 0.47 ns로 일별 편차가 낮게 나타났다. 반면, 태양활동이 활발했던 2023년의 연평균 DC 값은 8.88 ns로, 표준편차는 2.95 ns로 산출되었다. 태양활동이 활발해질수록 DC 값이 증가했으며, DC 값의 일별 편차가 크게 나타나는 것을 확인할 수 있었다. 분석 기간 동안 산출한 DC는 모두 LEG의 DC와 상이한 값을 가졌기 때문에, 기존 5 ns는 한반도 인근 지역에서 보편적으로 적용하기에는 한계가 있다.
모든 격자에서 LEG와 NEW의 VTEC을 계산한 후, GIM의 VTEC을 기준으로 RMSE를 미터(meter) 단위로 산출하여 정확도를 평가하였다. 2019년과 2023년의 일별 VTEC RMSE는 Figs. 4와 5에 제시하였다. 모든 일자에서 NEW로 산출한 VTEC RMSE는 기존 LEG의 VTEC RMSE보다 낮은 값을 보여 우수한 성능을 가지는 것을 확인할 수 있었다. 2019년에 LEG는 계절별로 편차를 나타냈으나, NEW는 계절에 관계없이 안정적인 성능을 보였다. 한편, 2023년에는 태양활동이 활발해짐에 따라 LEG와 NEW 모두 VTEC RMSE가 증가하였다. 특히 봄과 가을에 VTEC RMSE가 증가하는 경향이 관찰되었다. 이는 전리층 활동이 활발해지는 계절적 특성이 반영된 결과로 해석된다.
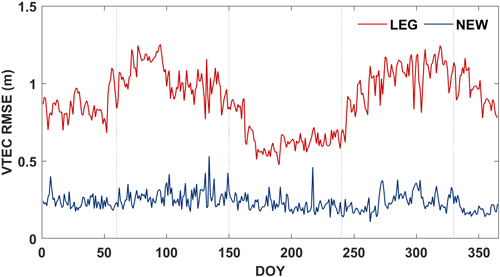
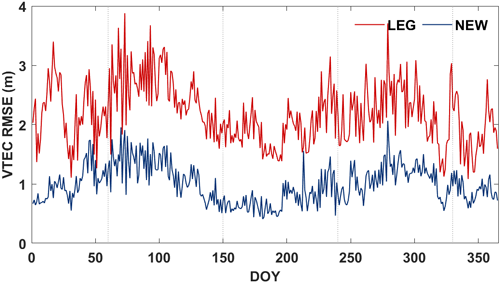
Table 1에는 Figs. 4와 5에 나타낸 2019년, 2023년의 일별 VTEC RMSE의 평균과 표준편차를 나타냈다. NEW의 평균값은 2019년과 2023년에 각각 0.23 m와 0.99 m로 모든 경우에서 1 m 이내의 값을 유지하였다. 이는 태양활동이 활발해지는 환경에서 LEG 기준 약 55%의 VTEC RMSE 성능 향상을 보인 것이다. 또한, NEW의 VTEC RMSE 표준편차는 2019년과 2023년에 각각 0.06 m와 0.33 m로 나타나, LEG에 비해 더 안정적으로 결과가 산출되는 것을 확인하였다.
table
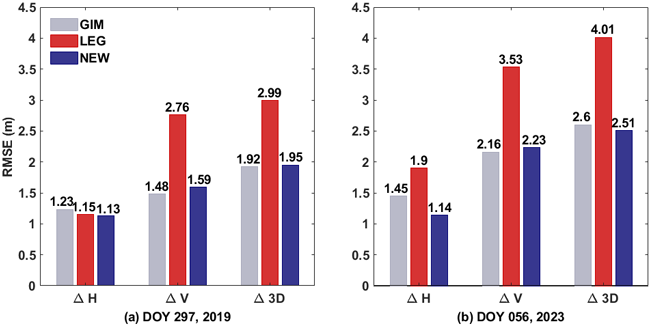
보정계수별 정확도를 비교하기 위해, 대전관측소(36.3994°N, 127.3745°E)에서의 GPS 단독의 Standard Point Positioning (SPP) 측위 결과를 분석하였다. 태양극소기인 2019년 중 태양활동이 가장 조용했던 일자인 DOY 297과, 2023년 태양극대기 중 태양 활동이 두 번째로 활발했던 DOY 056을 분석 일자로 선정하였다. 이는 F10.7이 가장 높았던 DOY 048이 연평균 수치에서 크게 벗어나는 값으로 기록되었기 때문에, 두 번째로 높은 값을 보인 DOY 056을 선택한 결과이다. Fig. 6에는 GIM, LEG, NEW의 측위 오차를 나타내었으며 Table 2에는 LEG 기준 NEW의 RMSE 향상률을 나타내었다.
Fig. 6a를 통해 수평방향으로는 모델별로 유사한 RMSE를 가졌지만, 수직 오차와 3차원 오차는 LEG의 정확도가 가장 낮아 NEW가 모든 방향에서 LEG의 정확도보다 우수한 것을 확인할 수 있었다. LEG 대비 NEW의 RMSE는 태양활동이 활발한 2023년 DOY 056의 경우 NEW는 수직방향과 3차원 방향에서 가장 우수한 성능을 보였다 (Fig. 6b). 특히 수직 방향에서는 LEG 기준 37.4%의 성능이 향상되었으며 3차원 오차는 GIM 대비 9 cm 감소하는 것을 확인할 수 있었다. 이를 통해 태양활동이 활발하더라도 NEW의 보정성능은 우수하게 나타나는 것을 확인하였다.
table
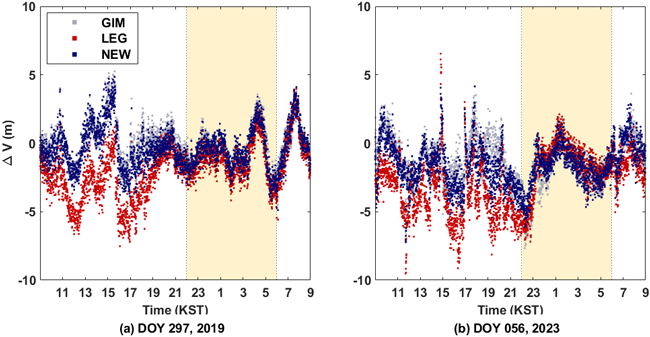
수평, 수직, 3차원 방향에 대한 24시간 동안의 RMSE 결과로 NEW의 성능을 확인할 수 있었다. 추가적으로 야간 시간대에서의 영향을 분석하기 위해 Klobuchar 모델에서 야간 시간으로 정의하는 22시부터 6시까지의 수직방향 오차를 분석하였다. Fig. 7에는 24시간 동안의 수직방향 오차를 나타냈으며, 노란색 박스로 야간 시간대를 구분하였다. 이를 통해 주간 시간대와 야간 시간대의 오차의 크기에 차이가 나타나는 것을 알 수 있었다. 특히, 빨간색 점으로 표시한 LEG의 경우 주간 시간대에 GIM과 NEW보다 수직 오차가 큰 값을 나타냈다. 이러한 경향은 야간 시간대에서도 유사하게 나타났다. 야간 시간대에서 NEW로 산출한 수직 오차는 GIM과 큰 차이가 나지 않았으며 LEG의 수직오차보다 작은 값을 가지는 것을 확인할 수 있었다. Table 3에는 야간 시간 동안의 수직방향에 대한 RMSE를 정리하였다. NEW RMSE는 2019년에 1.52 m, 2023년에 2.30 m로 산출되었다. NEW는 LEG 대비 20.4% (2019년), 7.3% (2023년) 향상된 것이다. 또한 2023년의 경우 GIM의 RMSE는 2.63 m로 나타났으며, 정확도가 모델 중 가장 낮은 것을 확인할 수 있었다. NEW는 GIM의 RMSE보다 33 cm 감소하여, 12.6%의 성능 향상을 나타냈다. 이를 통해 DC를 추정하는 것이 야간 시간대의 측위 성능을 향상시키는 데 기여할 수 있는 것으로 판단된다.
table
이 연구에서는 지역적 Klobuchar 모델의 정확도를 높이기 위해 IGS GIM을 이용하여 보정계수인
α
n
,
β
n
과 야간지연상수 DC를 동시에 추정하였다. 한반도에 위치하는 사용자를 가정했으므로 한반도 6개 지점에서 발생하는 IPP를 고려하여 격자점 120개를 선정하였다. 그리고 전체 격자점에서의 모델별 VTEC을 산출한 후 최소제곱법을 이용해 일별 보정계수와 DC를 추정하였다. 이 연구에서 추정한 보정계수의 정확도를 확인하기 위해 태양활동 1주기 중 태양극소기인 2019년과 태양극대기인 2023년을 선정하여, 태양활동을 대표하는 두 개의 연도를 분석 기간으로 설정하였다. 그 결과 태양활동의 강도에 따라 추정된 DC 값이 증가하거나 감소하는 양상을 보였다. 기존 DC 값인 5 ns와 새로 추정한 DC는 상이했기 때문에 DC를 5 ns로 고정하는 것은 한반도 인근 지역에 적합하지 않은 것으로 판단된다. 전체 격자점을 대상으로 IGS GIM 기준 VTEC RMSE를 산출한 결과, NEW는 LEG 대비 2019년, 2023년에 74.4%, 54.8%로 성능이 향상되었다. 그리고 NEW의 표준편차는 2019년과 2023년에 0.06 m, 0.33 m로, LEG에 비해 안정적으로 나타났다. 대전관측소에서의 측위정확도를 확인한 결과 NEW는 LEG 대비 수직방향으로 최대 47.9% 향상되었으며, 야간 시간대의 경우 최대 20.4% 향상되었다. 이 연구에서는 한반도에 한정하여 설정 격자점의 범위를 제한했지만, 사용자의 위치를 기반으로 유연하게 적용할 수 있기 때문에 활용 가능성이 높을 것으로 기대된다. 또한 이 연구에서는 GIM의 최종 산출물만을 이용하여 Klobuchar 모델의 보정계수와 DC를 추정했지만, 예측산출물을 이용한다면 실시간 적용이 가능할 것이라고 예상된다.
본 연구는 2025년도 국토교통부의 재원으로 국토교통과학기술진흥원의 지원으로 수행되었음 (RS-2022-00141819, 초정밀 디지털 국토정보 획득을 위한 절대, 상대, 연속복합 측위 고도화 기술 개발).
Conceptualization, E.-J. Sim and K.-D. Park; Methodology, E.-J. Sim and K.-D. Park; Software, E.-J. Sim; Validation, E.-J. Sim; Formal analysis, E.-J. Sim; Investigation, E.-J. Sim; Writing—original draft preparation, E.-J. Sim; Writing—review and editing, E.-J. Sim and K.-D. Park; Visualization, E.-J. Sim; Supervision, K.-D. Park.
The authors declare no conflict of interest.
International GNSS Service, Ionospheric Products [Internet], cited 2025 Jan 21, available from: https://igs.org/ products/#ionosphere
Klobuchar, J. A. 1987, Ionospheric time-delay algorithm for single-frequency GPS users, IEEE Transactions on aerospace and electronic systems, AES-23, 325-331. https://doi.org/10.1109/TAES.1987.310829
Misra, P. & Enge, P. 2006, Global positioning system: Signals, Measurements, and Performance, 2nd ed. (Lincoln, MA: Ganga-Jamuna Press).
Nishimoto, K., Ohashi, M., Kubo, Y., & Sugimoto, S. 2013, Refining the Klobuchar Ionospheric Model with Spherical Cap Harmonic Model for GNSS Positioning, Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications, 2013, 236-243. https://doi.org/10.5687/sss.2013.236
Park, K.-D., Sim, E.-J., Choi, B.-K., Sohn, D.-H., Chung, J.-K., et al. 2025, Generation of Klobuchar Coefficients based on IGS GIM for a Regionally Optimized Ionospheric Correction in GNSS Positioning [Manuscript in preparation]. Department of Geoinformatic Engineering, Inha University.
Schaer, S., Gurtner, W., & Feltens, J. 1998, IONEX: The Ionosphere Map Exchange Format Version 1, in Proceedings of the IGS AC Workshop, Darmstadt, Germany.
Sim, E.-J., Park, K.-D., Park, J.-Y., & Park, B.-G. 2023, Accuracy Analysis of Predicted CODE GIM in the Korean Peninsula, Journal of Positioning, Navigation, and Timing, 12, 423-430. https://doi.org/10.11003/ JPNT.2023.12.4.423
Wang, N., Li, Z., Yuan, Y., Li, M., Huo, X., et al. 2019, Ionospheric Correction Using GPS Klobuchar Coefficients with an Empirical Night-Time Delay Model, Advances in Space Research, 63, 886-896. https://doi. org/10.1016/j.asr.2018.10.006
Yuan, Y., Huo, X., Ou, J., Zhang, K., Chai, Y., et al. 2008, Refining the Klobuchar Ionospheric Coefficients Based on GPS Observations, IEEE Transactions on Aerospace and Electronic Systems, 44, 1498-1510. https://doi. org/10.1109/TAES.2008.4667725
Zhang, Q., Liu, Z., Hu, Z., Zhou, J., & Zhao, Q. 2022, A Modified BDS Klobuchar Model Considering Hourly Estimated Night-Time Delays, GPS Solutions, 26, 49. https://doi.org/10.1007/s10291-022-01236-0
Zhou, W., Song, S., Chen, Q., Cheng, N., & Xie, H. 2018, Determination of Nighttime VTEC Average in the Klobuchar Ionospheric Delay Model, Geodesy and Geodynamics, 9, 175-182. https://doi.org/10.1016/ j.geog.2017.09.001