Byung-Kyu Choi†, Dong-Hyo Sohn, Junseok Hong
Space Science Division, Korea Astronomy and Space Science Institute, Daejeon 34055, Korea
†Corresponding Author: Byung-Kyu Choi, E-mail: bkchoi@kasi.re.kr
Citation: Choi, B.-K, Sohn, D.-H., & Hong, J. 2025, Analysis and Comparison of PPP ZTD using Empirical Models GPT, GPT2, and GPT3, Journal of Positioning, Navigation, and Timing, 14, 21-28.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 March, Volume 14, Issue 1, pages 21-28. https://doi.org/10.11003/JPNT.2025.14.1.21
Received on Jan 21, 2025, Revised on Feb 03, 2025, Accepted on Feb 12, 2025, Published on Mar 15, 2025.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The accuracy of tropospheric delay corrections for the global navigation satellite system (GNSS) depends on the quality of the tropospheric model. The empirical tropospheric models used in GNSS processing include the Saastamoinen, global pressure and temperature (GPT), and global mapping function (GMF). In the present study, we estimate precise point positioning (PPP) zenith total delay (ZTD) using GPT, GPT2, and GPT3 empirical models, and then compare the results. To verify the PPP ZTD obtained from the GPT model, we compared it with the international GNSS service (IGS) ZTD products. The root mean square (RMS) value at the DAEJ station was estimated to be 4.97 mm. This is close to the accuracy of the IGS ZTD, which is about 4 mm. As a result, it is suggested that the PPP ZTD estimated in this study is reliable. In addition, we confirmed that there is a bias of 0.33 mm, 0.26 mm, and 0.49 mm between the GPT and other models at the DAEJ, MIZU, and DARW stations, respectively. On the other hand, no bias was observed between the GPT2 and GPT3 models, except for at DARW, and their ZTD values were in good agreement.
GNSS, ZTD, GPT, PPP
위치결정, 항법, 그리고 정밀시각 정보 제공을 위해 설계된 Global Navigation Satellite System (GNSS)는 대기 수증기량을 정밀 측정하는 시스템으로도 활용되고 있다. 전 지구에 고르게 분포하고 있는 GNSS 기준국들과 특정 지역에 조밀하게 분포하는 GNSS 기준국망은 데이터 가용성을 증가시키고 있다. 또한 GNSS는 높은 시간해상도를 갖고 있어서 15분 또는 그 이내에서 대기 수증기량을 측정할 수 있다. 따라서 GNSS는 대기 수증기량 변화를 연구하는데 매우 유용하다. GNSS가 전 지구, 대륙 또는 지역 단위에서 대기 수증기량을 정밀하게 측정한 여러 연구사례가 있다 (Bock et al. 2007, Wang & Zhang 2009, Vaquero-Martínez et al. 2018). GNSS 관측으로부터 계산된 수증기량은 라디오존데, 수치 기상 모델과 같은 타 기준 측정값과 비교를 통해 검증을 수행한다. 또한 GNSS 관측을 통한 수증기량의 정밀한 산출은 수치 예보능력 향상, 기후변화 감시 등에도 활용되고 있다 (Negusini et al. 2021).
최근에는 기후변화로 인해 국지적인 집중호우, 대형 태풍, 그리고 잦은 폭설 등 피해가 급증하고 있다. 이러한 피해를 일으키는 근본적인 원인은 대기중의 수증기라 할 수 있으며, 이를 정확하게 측정하고 감시하는 것이 필요하다.
GNSS는 대기 수증기량을 연속적으로 관측하는 도구로써 널리 활용되고 있다 (Bevis et al. 1992). 국제 GNSS 서비스국(International GNSS Service, IGS)은 전 지구적으로 고르게 분포하고 있는 IGS 기준국들의 관측자료를 이용해서 일일단위로 각 기준국에서의 zenith total delay (ZTD) 산출물을 제공한다. 또한 스위스 Center for Orbit Determination in Europe (CODE), 미국 Jet Propulsion Laboratory (JPL), 유럽 European Space Agency (ESA), 스페인 Universidad Politécnica de Cataluña (UPC), 그리고 중국 Wuhan University (WHU) 등과 같은 GNSS 분석센터에서도 별도로 기준국의 대류권 ZTD 산출물을 제공한다.
대류권에 의한 총 지연량은 일반적으로 ZTD로 표현된다. ZTD는 천정 건조 지연(zenith hydrostatic delay, ZHD)과 천정 습윤 지연(zenith wet delay, ZWD)으로 나누어진다. ZHD는 대기압(atmospheric pressure)과 온도에 의해 달라지고, ZWD는 부분 수증기압(partial water vapour pressure)과 온도에 따라 달라지기 때문에 대기 매개변수가 무엇보다도 중요하다 (Tang et al. 2013, Ding & Chen 2020). GNSS 기준국에서는 MET4 또는 MET4A와 같은 기상 관측장비를 설치하여 현장에서 직접 대기 매개변수를 측정할 수 있다. 그러나 기준국마다 기상 관측장비의 설치는 막대한 비용이 발생한다. 또한 일부 기준국에 이러한 장비의 설치는 공간 해상도를 떨어지게 할 수 있다. 따라서 경험적인 모델을 사용하여 대기 매개변수를 얻는 것이 유용할 수 있다 (Lagler et al. 2013).
대기 매개변수를 얻을 수 있는 대표적인 경험모델이 바로 Global Pressure and Temperature (GPT)이다. GPT 모델은 Böhm et al. (2007)에 의해 고안이 되었고, 최근까지 지속적으로 모델이 갱신되었다. 현재는 GPT, GPT2, GPT2w 그리고 GPT3 모델이 있다. GPT2w는 온도 감소율과 수증기의 평균 온도라는 두 개의 매개변수가 추가된 것 외에는 GPT2와 거의 차이가 없다. GPT3는 GPT2w의 업그레이드 버전으로 유럽중기 기상예보센터(European Center for Medium-Range Weather Forcasts, ECMWF) ReAnalyis (ERA)-Interim 데이터를 기반으로 개발되었다. GPT3에는 동쪽 경사도(East gradient)와 북쪽 경사도(North gradient) 매개변수가 추가되었다 (Landskron & Böhm 2018).
Böhm et al. (2007)은 간단한 모델을 사용하는 대신 GNSS 또는 초장기선 전파간섭계(very long baseline interferometry) 분석에서 대류권 모델링에 GPT 모델 사용을 권고한 바 있다. 최근에는 대류권을 분석하고 타 모델과 함께 활용하는 분야에 GPT3 모델이 많이 활동 되고 있다 (Ding & Chen 2020, Yang et al. 2021, Huang et al. 2023). 그러나 서로 다른 GPT 모델들을 GNSS PPP에 적용했을 때 대류권 ZTD 추정치의 차이와 이에 대한 분석을 수행한 연구는 찾아보기 어렵다.
따라서 본 연구에서는 GPT, GPT2, GPT3 모델에서 얻어진 대기 매개변수를 이용해서 대류권 ZTD를 추정하고 이에 대한 통계적인 분석 값을 제시한다.
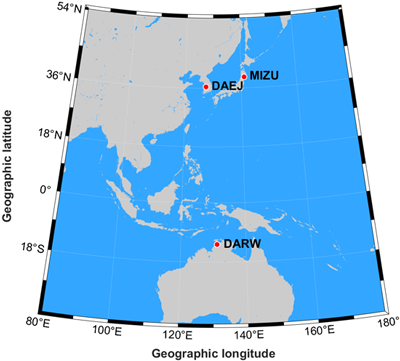
한반도 및 인근 지역에서 경험모델 GPT 계열의 대류권 ZTD 추정을 위해 세 곳의 IGS 기준국을 선정하였다. Fig. 1은 DAEJ, MIZU, 그리고 DARW 기준국의 위치 분포이다. 세 곳의 기준국에는 각각 Trimble NetR9과 Septentrio PolaRx5 수신기가 설치되어 있고, 추가적인 안테나 구성은 Table 1과 같다. 실험에 선정된 기준국들은 버전 3.0x 이상의 Receiver Independent Exchange Format (RINEX) 관측파일을 제공하고 있다. 이 파일에는 GPS, GLONASS, Galileo, BeiDou, 그리고 QZSS 항법 관측자료가 함께 포함되어 있다. 이러한 RINEX 파일은 IGS 데이터 센터(https://cddis.nasa.gov/archive/ gnss/data)에서 다운로드 할 수 있다. 또한 GNSS PPP 자료처리에 필요한 위성궤도, 위성시각 오차, 지구자전계수 산출물은 독일 지구물리연구소(GeoForschungsZentrum Potsdam, GFZ)에서 제공하는 Rapid 산출물을 사용한다. GFZ Rapid 산출물은 모든 위성항법시스템에 대한 정밀 위성궤도와 정밀 위성시각 정보를 포함하고 있다.
테이블
고정밀 GNSS 자료처리에서 대류권은 큰 오차로 작용한다. 전리층에 의한 오차는 이중주파수 관측치를 이용해서 약 99% 이상 제거할 수 있지만, 대류권 오차는 직접 추정하거나 경험식을 이용해서 계산해야만 한다 (Niell 1996).
일반적으로 GNSS 대류층 지연오차를 추정하는 것은 식 (1)과 같이 표현할 수 있다 (Davis et al. 1985).
수식
여기서
Δ
T
h
z
와
Δ
T
w
z
는 각각 천정방향 건조지연(zenith hydrostatic delay)과 천정방향 습윤지연(zenith wet delay)을 의미한다.
m
f
h
(
ε
)
와
m
f
w
(
ε
)
은 각각 건조지연과 습윤지연의 사상함수(mapping function)이며, 본 연구에서는 사상함수로 global mapping function (GMF)을 사용한다 (Böhm et al. 2006). 그리고
ε
는 수신기와 위성의 위치로 계산되는 위성의 앙각(elevation angle)이다.
건조지연은 Saastamoinen 모델을 이용해서 쉽게 계산할 수 있으며, 식 (2)와 같다 (Davis et al. 1985).
수식
여기서 p는 GPT 모델로부터 얻어지는 기준국에서의 대기압력이다.
φ
는 기준국의 위도,
h
e
l
l
은 기준국의 고도값이다.
건조지연에 비해 습윤지연을 정확하게 추정하는 것은 매우 어렵다. 습윤지연량은 건조지연량의 10~20% 수준이지만 GNSS PPP에 큰 오차요인으로 작용한다. 특히 이것은 고정밀 측지/측량 등에서 고도방향 위치오차에 직접적인 영향을 준다. 본 연구에서는 GNSS PPP 기법을 이용해서 천정방향 습윤지연량을 추정한다.
Table 2는 대류권 ZTD를 추정하기 위한 자료처리 방법과 모델들을 기술한 것이다. 자료처리에 사용된 위성항법시스템은 GPS, GLONASS, Galileo, BeiDou, 그리고 QZSS이다. 즉, 기준국에서 수신되는 모든 항법위성의 관측치를 사용한다. 정밀한 ZTD를 추정하기 위해서는 반드시 이중주파수 관측자료가 필요하다. 본 연구에서 GPS는 L1C와 L2W, GLONASS는 L1C와 L2C를 사용하였다. GLONASS의 L2C 관측자료가 없는 경우에는 대체 신호로 L2P 신호 사용을 고려하였다. 수신기 제조사 별로 제공하는 일부 신호 타입이나 관측자료가 상이하기 때문에 대체 신호 사용을 고려할 필요가 있다. Galileo는 L1C와 L5Q를 우선순위 신호로 설정하였고, L1C가 없는 경우 L1P 또는 L1X를 사용하도록 설정하였다. 또한 L5Q가 없는 경우에는 대체신호로 L5X를 이용한다. BeiDou는 L1C와 L7I 신호를 우선 사용하도록 설정하고, L1C가 없는 경우에는 L1P와 L1I를, 그리고 L7I가 없는 경우에는 L7D를 대체 사용한다. QZSS는 L1C와 L5Q 신호를 사용하도록 설정하며, L5Q가 없는 경우에는 대체신호로 L5P와 L5X 신호를 사용한다.
테이블
대류권의 천정방향 습윤지연 오차는 동쪽(Ge)과 북쪽(Gn) 방향 경사도(gradient) 매개변수와 함께 추정을 한다. 이때 사용하는 사상함수로는 GMF를 사용하고, 추가적으로 GPT, GPT2, GPT3 모델에서 얻어진 대기 매개변수를 이용해서 최종 ZTD를 산출한다.
GNSS 상태변수 추정을 위한 자료처리 방법은 ‘static’, ‘kinematic’, ‘dynamic’ 형태로 구분할 수 있다. 정밀한 대류권 ZTD 추정을 위해서 일반적으로 ‘static’ 방법을 사용한다. 이 연구에서도 상태변수 추정을 위해 ‘static’ 방법을 사용하였다.
GPT 모델은 ECMWF 40년 재해석 데이터(ERA-40)의 압력과 온도에 대한 정보를 이용해서 만들어진 것이다 (Uppala et al. 2005). 과거에는 ERA-15로 자료가 제공되었고, 최근에는 압력과 온도에 대한 정보가 ERA-Interim으로 통합 제공되고 있다. 이것은 압력과 온도에 대한 월 평균 프로파일과 전지구 위도·경도 격자해상도(
15
o
×
15
o
)에 대한 3년치(1999년 9월부터 2002년 8월)를 기반으로 한다. 즉, 각 격자점에 대해 평균해수면에서의 압력과 온도에 대한 월 평균값 36개를 사용한다. 이에 대한 구체적인 표현은 식 (3)과 같다.
수식
여기서
r
(
t
)
는 기상 매개변수로 압력과 온도이고,
d
o
y
는 연중 일수(day of year)를 의미한다.
A
0
는 평균 값이고, 연간 진폭
A
는 위상 옵셋이
d
o
y
가 연중 일인 1월 28일에 고정되어 추정된다 (Niell 1996).
Lagler et al. (2013)은 GPT와 GMF를 개선하고 결합한 후 업데이트된 블라인드 모델을 GPT2라고 명명했습니다. 그들은 ERA-Interim 재해석에서 얻은 10년(2001년~2010년)의 월 평균 기압 수준 데이터를 사용하였다. 그리고 평균 Earth Topography Five Minute Grid (ETOPO5) 높이와 규칙적인
5
o
×
5
o
격자에서 선택된 매개변수 r(t)에 대한 평균값,
A
0
와 연간 진폭(annual amplitude)인
A
1
과
B
1
그리고 반기별 진폭(semi-annual amplitude)인
A
2
와
B
2
를 함께 결정했다. 식 (4)를 이용해서 GPT2 매개변수를 계산할 수 있다 (Zhu et al. 2022).
수식
GPT3 모델은 이전 모델인 GPT2에서 채택하고 있는 일련의 기상학적 양이 포함되어 있다. GPT3 모델은 측지, 기상, 기후 연구 목적으로 사용할 수 있는 매우 포괄적인 대류권 모델이다. GPT3 모델은
5
o
×
5
o
와
1
o
×
1
o
의 격자 데이터를 제공하는 경험적 모델이다. GPT3는 이전 모델인 GPT2와 매우 유사하지만,
1
o
×
1
o
의 격자 버전을 사용하여 더 나은 결과를 제공하고 있다 (Landskron & Böhm 2018). 그리고 이 모델은 온도, 압력, 수증기압과 같은 기상 데이터를 제공하는 것 외에도 수증기의 평균온도(
T
m
) 값을 계산하는데 사용할 수 있다. 본 연구에서는 GPT3 모델의
1
o
×
1
o
의 격자 데이터를 사용했다. 또한 매개변수를 추정하는 방법은 GPT2와 같은 식 (4)를 사용한다.
대류권 ZTD의 추정 정확도에 큰 영향을 주는 매개변수가 온도와 대기압력이다. 경험적 모델들로 산출되는 값을 비교하기 위해 먼저 2024년 일년간 DAEJ 기준국에서의 일일 평균 온도와 대기압력을 생성하였다. Fig. 2는 2024년 DOY로 1일부터 366일까지 GPT, GPT2, 그리고 GPT3 모델을 이용해서 산출한 일일 평균 온도와 대기압력에 대한 시계열을 보여주고 있다. 온도 변화와 대기압력 변화는 각각 Figs. 2a,b에서 볼 수 있다. Fig. 2a에서 붉은색, 파란색, 연두색 실선으로 표기된 것은 GPT, GPT2, GPT3 모델에서 각각 산출한 평균 온도이다. Fig. 2a에서 볼 수 있듯이 모델들은 일일 평균온도가 DOY 20에서 50일 사이에 최솟값을, DOY 210에서 230일 사이에 최댓값을 보이고 있다. 특히 GPT2와 GPT, 그리고 GPT3와 GPT 모델 간 평균 온도의 최대 차이는 각각 2.1도와 2.7도로 나타났다.
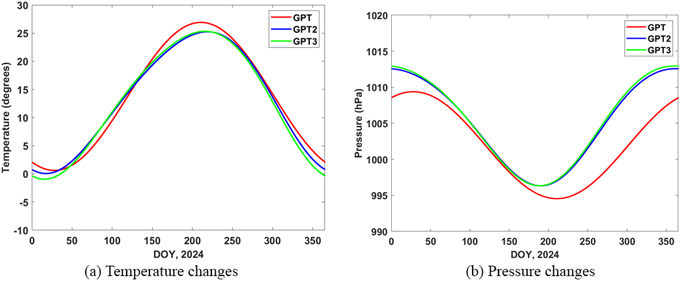
DAEJ 기준국의 대기압력은 약 995 헥토파스칼(hectopascal, hPa)에서 1013 hPa 내에서 형성이 되며, Fig 2a의 평균 온도변화 그래프와는 반대되는 경향을 보인다. GPT2와 GPT, 그리고 GPT3와 GPT 모델 간 대기압력의 최대 차이는 각각 7.2 hPa과 7.6 hPa이다.
또한 GPT2와 GPT3 모델에서 각각 산출된 평균 온도와 대기압력은 그 차이가 최대 0.4도와 1.1 hPa로 두 모델 간에는 큰 차이가 없음을 알 수 있었다.
경험적 모델인 GPT로부터 산출된 평균 온도와 대기압력 값을 GNSS PPP 자료처리에 적용하여 ZTD 값을 산출하였다. 모델간 평균 온도와 대기압력 차이가 큰 2024년 DOY 306일부터 336일까지 DAEJ, MIZU, 그리고 DARW 기준국의 관측자료를 처리하였다. 그리고 PPP로 추정된 ZTD 값의 검증을 위해 IGS에서 제공하는 ZTD 산출물과 비교하였다. IGS에 등록된 GNSS 기준국들의 ZTD 산출물은 데이터센터 (https://cddis.nasa.gov/archive/gnss/products/troposphere/zpd/)에서 다운로드 하였다.
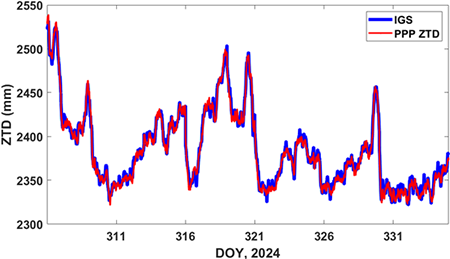
Fig. 3은 IGS ZTD 산출물과 PPP로부터 얻어진 ZTD 시계열을 함께 보여주고 있다. Fig. 3에서 파란색 실선과 붉은색 실선은 각각 IGS ZTD와 PPP ZTD를 의미한다. Table 3에 나타낸 것처럼, 본 연구에서 산출한 DAEJ 기준국의 PPP ZTD 값은 IGS ZTD와 비교하여 그 차이에 대한 평균값은 -0.14 mm 그리고 root mean square (RMS) 값은 4.97 mm였다. IGS ZTD의 정확도는 4 mm 수준으로 알려져 있다 (https://www.igs.org/products). PPP ZTD에 의해 산출된 수치들은 IGS ZTD의 정확도와 매우 유사한 수준이다. 따라서 본 연구에서 추정한 PPP ZTD가 신뢰할 만한 수준임을 알 수 있다.
테이블
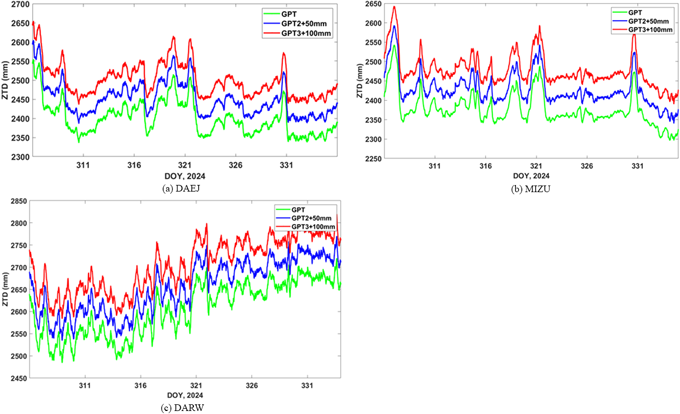
Fig. 4는 서로 다른 GPT 모델들(GPT, GPT2, GPT3)을 이용해서 추정한 ZTD 시계열을 나타낸 것이다. Fig. 3과 동일하게 PPP ZTD 추정을 위해 각각 GPT, GPT2, GPT3 모델에서 생성된 매개변수를 사용하였다. 서로 다른 모델들에 의해 추정된 ZTD 값은 Fig. 4에 붉은색 실선, 파란색 실선, 그리고 녹색 실선으로 표기를 했다. 그리고 GPT2와 GPT3 모델로부터 산출된 ZTD값은 자료처리 결과의 뚜렷한 구분을 위해 각각 +50 mm와 +100 mm의 편향(bias) 값을 추가하였다. Figs. 4a-c는 각각 DAEJ, MIZU, 그리고 DARW 기준국에서 산출된 PPP ZTD를 나타낸 것이며, GPT 모델 간에는 동일한 경향성을 보이고 있다.
서로 다른 모델들을 이용해서 산출한 ZTD 값들의 차이를 분석하기 위해 GPT2와 GPT, GPT3와 GPT, 그리고 GPT3와 GPT2 모델 간의 ZTD 값 차이를 각각 계산하였고, 그것들을 Fig. 5에 나타냈다. Fig. 5a의 a)-c)는 DAEJ 기준국에서 GPT2와 GPT, GPT3와 GPT, 그리고 GPT3와 GPT2 모델 간의 ZTD 차이를 각각 나타낸 것이다. 해당기간 동안 GPT2와 GPT의 ZTD 값은 ±3 mm 내에서 차이가 있었다. 또한 GPT3와 GPT의 차이는 앞선 GPT2와 GPT의 차이와 매우 유사한 것을 알 수 있다. 그리고 Fig. 5a의 c)에서 볼 수 있듯이 GPT3와 GPT2 모델은 ZTD 값에 차이가 없는 것으로 나타났다. Fig. 5b는 MIZU 기준국에서의 모델 간 ZTD 값 차이를 나타낸 것이며, Fig. 5a의 DAEJ 기준국의 결과와 매우 유사한 특징을 보인다. Fig. 5c는 남반구에 위치한 DARW 기준국의 결과를 보여주고 있다. DARW에서 GPT2와 GPT, GPT3와 GPT 모델 간 차이는 앞선 두 곳의 기준국과 유사하지만, GPT3와 GPT2는 평균 -0.16 mm로 조금 편향된 값을 보였다.
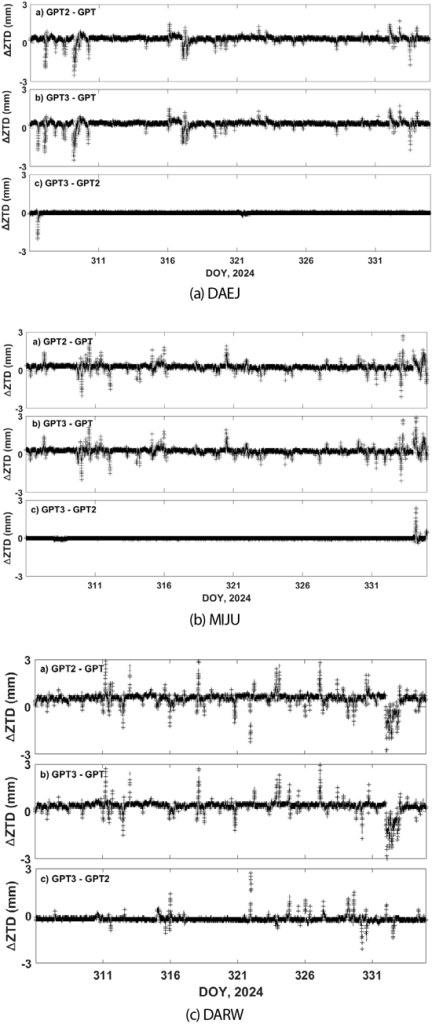
Table 3은 세 곳 기준국(DAEJ, MIZU, DARW)의 결과로부터 얻은 모델 간의 통계적인 값을 나타낸 것이다. DAEJ 기준국에서는 GPT2와 GPT, GPT3와 GPT 모델 간에 약 0.33 mm의 편향(bias)되는 특징을 보였다. MIZU 기준국에서는 DAEJ와 유사하게 서로 다른 두 모델 간에 약 0.26 mm의 편향성이 나타났다. 반면 DAEJ와 MIZU 기준국에서 GPT3와 GPT2 모델은 서로 편향되지 않았으며, RMS 값도 각각 0.06 mm와 0.08 mm로 잘 일치했다. DARW 기준국에서는 중위도에 위치한 DAEJ와 MIZU와는 달리 GPT3와 GPT2 모델 간에 약 -0.16 mm의 차이가 있었다. 그러나, 이러한 차이는 매우 작다. GPT3와 GPT2 모델은 모델 생성 및 분석을 위한 기간이 동일하며, 격자 해상도 및 일부 매개변수의 추가 이외에는 거의 유사하다 (Landskron & Böhm 2018).
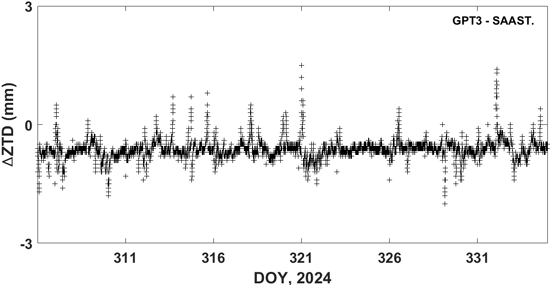
Fig. 6은 GPT3 모델로부터 산출된 ZTD와 Saastamoinen 기본 모델의 대기 매개변수로부터 산출된 ZTD의 차이를 시계열로 나타낸 것이다. GPT3 모델을 사용하지 않는 경우 Saastamoinen 모델의 입력 값으로 평균 온도와 대기압력은 각각 섭씨 15도와 1013.25 hPa를 사용하였다. Fig. 6은 DAEJ 기준국에서의 두 모델간 ZTD 차이를 의미한다. DAEJ 기준국에서는 GPT3와 Saastamoinen 모델간 ZTD가 평균적으로 약 0.63 mm 편향되는 것으로 나타났다. ZTD 차이에 대한 RMS 값은 0.67 mm로 편향된 값과 유사했다. ZTD 편향은 GPT3 모델로부터 산출된 대기 매개변수와 Saastamoinen 모델에서 설정한 기본 매개변수와의 차이가 원인 일 수 있다.
본 연구결과로부터 여러 경험적 GPT 모델에서 생성되는 대기 매개변수는 정밀한 대류권 ZTD 추정에 약간의 편향을 발생시킬 수 있다는 것을 알 수 있었다.
본 연구에서는 경험적 모델인 GPT, GPT2, 그리고 GPT3 모델을 PPP ZTD 값 산출에 이용하여 서로 비교 분석하였다. 먼저 GPT, GPT2, GPT3 모델로부터 생성되는 대기 매개변수인 온도와 대기압력을 분석하였고, DAEJ 위치 기준으로 모델간 온도는 최대 약 2.7도, 대기압력은 최대 약 7.6 hPa의 차이가 있었다.
또한 GPT 모델을 이용한 PPP ZTD 값의 검증을 위해 IGS ZTD 산출물과 비교하였다. DAEJ 기준국은 RMS 값이 4.97 mm로 추정되었고, 이것은 IGS ZTD의 정확도인 4 mm와 매우 유사하여 본 연구에서 추정한 PPP ZTD가 신뢰할 만한 수준임을 제시하였다.
서로 다른 세개의 모델을 이용해서 PPP ZTD를 산출하였고, 각 모델의 매개변수를 이용해서 산출한 PPP ZTD 값을 서로 교차 비교하였다. 결과적으로 DAEJ, MIZU, 그리고 DARW 기준국에서는 GPT2와 GPT, GPT3와 GPT 모델 간에 0.33 mm와 0.26 mm의 편향이 나타난 것을 확인했다. 그리고 DAEJ와 MIZU에서는 GPT3와 GPT2 모델 간에는 편향이 나타나지 않았고, ZTD 값의 차이가 없었다. 반면에 DARW에서는 GPT3와 GPT2 모델 간에는 -0.16 mm 편향이 나타났고, 이 값은 매우 미비한 수준이다.
본 연구는 GNSS PPP 자료처리시에 대류권 ZTD 추정을 위해 사용하는 경험적 모델인 GPT, GPT2, 그리고 GPT3 모델 간의 차이를 비교 분석했으며, GNSS 대류권 연구에 도움이 될 수 있을 것으로 판단한다.
This study was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 2025-1-8-5004) supervised by the Ministry of Science and ICT.
Methodology, B.-K. Choi, D.-H. Sohn and J. Hong; software, B.-K. Choi; formal analysis, B.-K. Choi; investigation, D.-H. Sohn and J. Hong.
The authors declare no conflict of interest.
Bevis, M., Businger, S., Herring, T. A., Rocken, C., Anthes, R. A., et al. 1992, GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System, J. Geophys. Res., 97, 15787. https://doi. org/10.1029/92JD01517
Bock, O., Guichard, F., Janicot, S., Lafore, J. P., Bouin, M. N., et al. 2007, Multiscale analysis of precipitable water vapor over Africa from GPS data and ECMWF analyses, Geophys. Res. Lett., 34. https://doi. org/10.1029/2006GL028039
Böhm, J., Heinkelmann, R., & Schuh, H. 2007, Short Note: A global model of pressure and temperature for geodetic applications, J. Geod., 81, 679-683. https://doi. org/10.1007/s00190-007-0135-3
Böhm, J., Niell, A., Tregoning, P., & Schuh, H. 2006, Global Mapping Function (GMF): a new empirical mapping function based on numerical weather model data, Geophys. Res. Lett., 33. https://doi.org/:10.1029/ 2005GL025546
Davis, J. L., Herring, T. A., Shapiro, I. I., Rogers, A. E. E., & Elgered, G. 1985, Geodesy by radio interferometry: effects of atmospheric modeling errors on estimates of baseline length, Radio Sci., 20, 1593-1607. https://doi. org/10.1029/RS020i006p01593
Ding, J. S. & Chen, J. P. 2020, Assessment of empirical troposphere model GPT3 based on NGL’s global troposphere products, Sensors, 20, 3631. https://doi. org/10.3390/s20133631
Huang, L., Zhu, G., Peng, H., Liu, L., Ren, C., et al. 2023, An improved global grid model for calibrating zenith tropospheric delay for GNSS applications, GPS Solut., 27, 17. https://doi.org/10.1007/s10291-022-01354-9
Lagler, K., Schindelegger, M., Böhm, J., Krasna, H., & Nilsson, T. 2013, GPT2: Empirical slant delay model for radio space geodetic techniques, Geophys. Res. Lett., 40, 1069-1073. https://doi.org/10.1002/grl.50288
Landskron, D. & Böhm, J. 2018, VMF3/GPT3: refined discrete and empirical troposphere mapping functions, J. Geod., 92, 349-360. https://doi.org/10.1007/s00190017-1066-2
Negusini, M., Petkov, B. H., Tornatore, V., Barindelli, S., Martelli, L., et al. 2021, Water Vapour Assessment Using GNSS and Radiosondes over Polar Regions and Estimation of Climatological Trends from Long-Term Time Series Analysis, Remote Sens., 13, 4871. https:// doi.org/10.3390/rs13234871
Niell, A. E. 1996, Global mapping functions for the atmosphere delay at radio wavelengths, JGR, 101, 32273246. https://doi.org/10.1029/95JB03048
Tang, Y. X., Liu, L., & Yao, C. 2013, Empirical model for mean temperature and assessment of precipitable water vapor derived from GPS, Geodesy and Geodynamics, 4, 51-56. https://doi.org/10.3724/SP.J.1246.2013.04051
Uppala, S. M., Kållberg, P. W., Simmons, A. J., Andrae, U., da Costa Bechtold, V., et al. 2005, The ERA-40 re-analysis, Q. J. R. Meteorol. Soc., 131, 2961-3012, https://doi. org/10.1256/qj.04.176
Vaquero-Martínez, J., Antón, M., Ortiz de Galisteo, J. P., Cachorro, V. E., Álvarez-Zapatero, P., et al. 2018, Intercomparison of integrated water vapor from satellite instruments using reference GPS data at the Iberian Peninsula, Remote Sens. Environ., 204, 729-740. https://doi.org/10.1016/j.rse.2017.09.028
Wang, J. & Zhang, L. 2009, Climate applications of a global, 2-hourly atmospheric precipitable water dataset derived from IGS tropospheric products, J. Geod., 83, 209-217. https://doi.org/10.1007/s00190-008-0238-5
Wu, J., Wu, S., Hajj, G., Bertiger, W., & Lichten, S. 1993, Effects of antenna orientation on GPS carrier phase, Manuscripta Geodaetica, 18, 91-98. https://doi. org/10.1007/BF03655303
Yang, X., Jiang, X., Jiang, C., & Xu, L. 2021, Real-Time Modeling of Regional Tropospheric Delay Based on Multicore Support Vector Machine, Mathematical Problems in Engineering, 2021, Article ID 7468963, 14, https://doi.org/10.1155/2021/7468963
Zhu, G., Huang, L., Yang, Y., Li, J., Zhou, L., et al. 2022, Refining the ERA5-based global model for vertical adjustment of zenith tropospheric delay, Satellite Navigation, 3, 27, https://doi.org/10.1186/s43020-02200088-w