1Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
2PP-Solution Inc., Seoul 08504, Korea
†Corresponding Author: Kwan-Dong Park, E-mail: kdpark@inha.ac.kr
Citation: Lee, J.-S., Park, K.-D., Park, B.-G., & Kim, M. 2025, Development of a Weighting Model Based on C/N0 and Code Pseudorange Residuals for Smartphone GNSS Positioning, Journal of Positioning, Navigation, and Timing, 14, 11-19.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 March, Volume 14, Issue 1, pages 11-19. https://doi.org/10.11003/JPNT.2025.14.1.11
Received on Jan 16, 2025, Revised on Jan 31, 2025, Accepted on Feb 13, 2025, Published on Mar 15, 2025.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
With the availability of smartphone GNSS raw measurement data, research on enhancing positioning accuracy using smartphones has become increasingly prominent. Despite the widespread use of C/N0-based weighting models to mitigate multipath errors, these models do not sufficiently account for the intrinsic characteristics of the observations, resulting in unstable positioning accuracy. To address this limitation, this study proposes a novel weighting model that incorporates the inherent characteristics of GNSS observations by combining code pseudorange residuals and C/N0. The proposed model utilizes a sliding window technique to calculate residuals through curve fitting of code pseudorange observations. These residuals are then combined with C/N0 to better reflect the unique features of the observations. Experimental results from tests conducted at Inha University demonstrate significant improvements in positioning accuracy. The proposed model achieved 40%, 32%, and 33% improvements in horizontal positioning accuracy and 32%, 20%, and 23% improvements in vertical accuracy for DOY 022, DOY 058, and DOY 253, respectively, compared to conventional elevation-based and C/N0-based models. These findings confirm that the proposed approach effectively improves both the accuracy and precision in smartphone GNSS positioning by addressing both observation noise and signal quality.
smartphone GNSS, C/N0 , observation noise, code pseudorange residuals
2016년 Google이 Android 7.0 운영체제를 출시하면서, 스마트폰에서 Global Navigation Satellite System (GNSS)의 원시데이터를 사용자에게 제공하기 시작했다 (Håkansson 2019). 이는 기존의 Position, Velocity and Time (PVT) 정보에 더해 코드의사거리, 반송파 위상, 도플러 관측치 등의 원시데이터를 제공함으로써 더욱 정밀한 위치 추정을 가능하게 만들었다 (Fortunato et al. 2019).
그러나 스마트폰 GNSS는 저가의 GNSS 칩셋과 선형 편광 방식의 안테나를 탑재하고 있어 다중경로 오차와 관측 잡음에 취약한 구조적 한계를 지니고 있다 (Yun et al. 2022). 일반 GNSS 수신기와 비교하였을 때, 스마트폰의 Carrier-to-Noise Density Ratio (C/N0)는 약 10 dB-Hz 정도 낮아 신호 강도가 약하고 잡음 수준이 높다 (Zangenehnejad & Gao 2021). 더불어 스마트폰의 반송파 위상 관측값은 잦은 불연속성과 빈번한 데이터 누락이 발생하여 연속적인 신호 처리와 정밀한 위치 추정을 어렵게 만든다. 이러한 기술적 한계를 극복하고 위치 추정 성능을 향상시키기 위해서는 스마트폰 GNSS의 특성을 반영하는 확률적 모델이 필요하다.
기존 연구에서는 GNSS 관측값의 품질에 따라 가중값을 부여하는 다양한 확률적 모델이 제안되었다. 스마트폰 GNSS의 경우, 위성 고도각 기반 가중값 모델이 아닌 C/N0 기반 가중값 모델이 적합하다고 평가되고 있다. Bahadur & Schön (2024)는 스마트폰 환경에 맞도록 수정된 C/N0 기반 가중값 모델과 Robust Kalman Filter를 설계하였고 이를 통해 관측값의 확률적 특성을 평가하고 이상치를 줄여 3D 위치 정확도를 기존 고도각 기반 모델 대비 약 45% 향상시켰다. 또한, 고도각 기반 모델과 C/N0 기반 모델을 결합하여 측위 정확도를 향상시키려는 연구도 있었다. Li et al. (2022)는 고도각과 C/N0 기반 가중값 모델을 결합하여 각 모델의 장점을 융합함으로써 개활지에서 고도각 기반 모델 대비 3D 위치 정확도를 약 22% 향상시켰다. Zangenehnejad & Gao (2023)은 최소 제곱 분산 성분 추정(LS-VCE) 기법을 사용하여 GNSS 관측값의 분산과 공분산을 추정하고 이를 기반으로 C/N0와 고도각을 결합한 확률적 모델을 설계하였다. 해당 연구에서 제안된 모델을 Precise Point Positioning (PPP)에 적용하였을 때, 수평 위치 정확도가 약 25% 향상되었다.
앞서 기술한 선행 연구들은 스마트폰 GNSS의 다중경로 오차와 관측 잡음 문제를 해결하기 위해 C/N0와 고도각을 활용한 확률적 모델을 제안하였다. 이러한 신호 품질 지표는 환경적 요인을 반영하는 데 효과적이지만 관측값 자체의 특성을 충분히 고려하지 못한다는 한계를 가진다. 따라서 본 연구에서는 스마트폰 GNSS 관측값 자체의 특성을 반영하여 관측 잡음과 신호 품질을 종합적으로 평가할 수 있는 새로운 확률적 모델을 제안한다. 연구에 사용된 Samsung Galaxy S21+의 코드의사거리 관측값에 슬라이딩 윈도우 기반 2차 다항식 곡선 접합 기법을 적용하여 각 윈도우 내 관측값의 변화를 모델링하였다. 이후, 모델로부터 계산된 잔차와 C/N0를 결합함으로써 다중경로 오차와 관측 잡음을 통합적으로 고려하는 새로운 가중값 모델을 설계하였다.
이 논문의 2장에서는 스마트폰 GNSS에 적합한 확률적 모델을 설계하기 위해 데이터의 품질 및 잡음 특성을 분석한다. 3장에서는 기존의 가중값 모델의 구조와 그 한계를 기술하고, 4장에서는 코드의사거리 기반 다항식 곡선 접합 방법과 C/N0와의 결합 기법에 대해 설명한다. 5장에서는 제안된 가중값 모델의 성능을 입증하기 위한 실험 결과를 다루며, 마지막으로 6장에서는 분석 결과와 향후 연구 방향에 대해 논의한다.
이번 장에서는 스마트폰 GNSS에 적합한 확률적 모델을 설계하기 위해 관측 데이터의 기본적인 품질과 잡음 수준을 확인한다. 2.1절에서는 데이터 취득 과정에 대해 기술하며, 2.2절에서는 일반 GNSS 수신기와 스마트폰에서 고도각, C/N0의 상관관계를, 2.3절에서는 관측 잡음의 특성을 분석한다.
스마트폰 GNSS 데이터의 품질과 잡음 수준을 분석하기 위해 2024년 9월 1일(DOY 253), 인하대학교 농구장에서 Samsung Galaxy S21+와 (주)피피솔의 RTAP2U 수신기를 이용해 30분간 데이터를 동시 취득하였다. 테스트 환경은 Fig. 1과 같으며, 관측 데이터는 Google의 GNSS Logger를 사용하여 기록하였다.

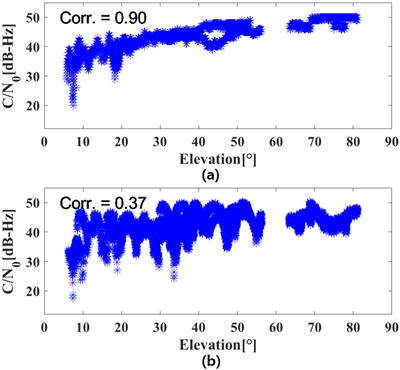
일반 GNSS 수신기는 다중경로 오차를 최소화하고 낮은 고도각에서도 신호를 효과적으로 수신하기 위해 우측 원형 편광 안테나(RHCP)를 사용한다. 반면 스마트폰은 설계와 크기 제한으로 인해 선형 편광 안테나를 사용하며 다중경로 오차와 신호 강도 저하에 취약하다 (Bisnath & Aggrey 2024). 이러한 안테나 설계의 차이는 위성 고도각과 C/N0의 상관관계에서 명확히 나타난다. Fig. 2는 Fig. 1의 환경에서 일반 수신기(Fig. 2a)와 스마트폰(Fig. 2b)으로 30분간 데이터를 직접 수집한 결과로, 위성 고도각과 C/N0의 상관관계를 보여준다. 일반 수신기는 고도각이 증가함에 따라 C/N0도 증가하며, 상관계수는 0.86으로 높은 상관성을 나타냈다. 반면 스마트폰은 고도각과 C/N0 간 상관성이 불규칙하며, 상관계수는 0.37로 일반 수신기에 비해 상당히 낮았다.
코드의사거리 관측값은 일반적으로 반송파 위상에 비해 약 100배 높은 수준의 관측 잡음을 포함한다. 특히 스마트폰 관측의 경우, 저가의 GNSS 안테나로 인해 신호 강도가 낮아 관측 잡음이 수시로 증폭된다.
이 연구에서는 일반 수신기와 스마트폰의 관측 잡음 수준을 비교하기 위해 시간 차분된 Code Minus Carrier (CMC)를 이용하였다. CMC는 코드의사거리와 반송파 위상 관측값의 차이를 계산한 값으로 관측값의 잡음 특성을 분석하는 데 활용된다. 시간 차분된 CMC는 Eq. (1)과 같이 구할 수 있다.
수식
여기서 t는 GPS seconds를 의미하며, i와 i-1은 현재 관측 시점과 이전 관측 시점을 의미한다. △CMC는 CMC의 변화율을 의미하며 시간에 따른 잡음의 차이를 분석하는데 용이하다. 본 연구에서 사용한 데이터는 1초 간격이므로 직관적인 분석을 위해 △ CMC를 m/s가 아닌 m 단위로 표기한다.
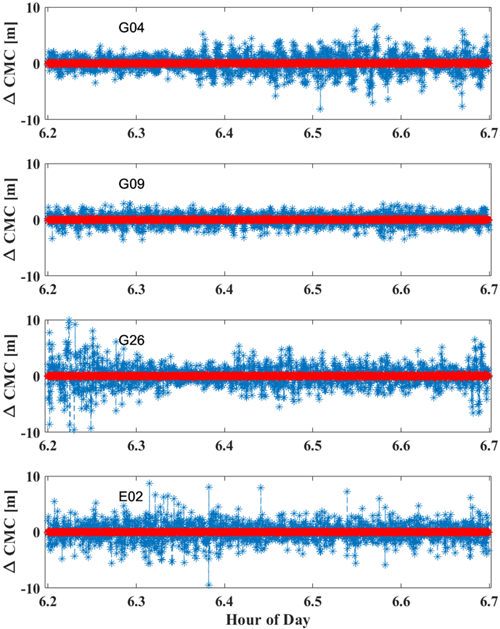
Fig. 3은 일반 수신기와 스마트폰의 △CMC 결과를 비교한 그래프이다. 일반 수신기의 경우,
△
CMC 값이 관측 시간 동안 일정하여 유지되어 신호 품질이 안정적인 것을 알 수 있다. 반면, 스마트폰은 관측 시간 동안 관측값에 일정 수준의 잡음이 포함되어 있으며 특정 시간대에
△
CMC 값이 크게 증가하는 경향을 확인할 수 있다. 이러한 경향은 위성 별
△
CMC의 분산과 RMS를 나타낸 Table 1에서도 확인할 수 있다.
table
일반 수신기의
△
CMC 분산은 0.001~0.015 m이며, RMS는 0.035~0.122 m이다. 반면 스마트폰의
△
CMC 분산은 0.397~2.779 m이며, RMS는 0.860~1.986 m로 일반 수신기에 비해 현저히 높은 잡음을 보여준다. 2장의 결과는 스마트폰 GNSS의 잡음 수준과 신호 품질 문제를 보완하기 위한 새로운 확률적 모델 개발의 필요성을 시사한다.
위성의 고도각에 기반한 가중값 모델은 코드의사거리 관측값의 잡음 수준을 설명하는데 주로 활용된다. 고도각이 높은 위성일수록 다중경로 오차 및 대기 오차의 영향이 적으며 신호 품질이 상대적으로 우수하다는 특징이 있다. 고도각 기반 가중값 모델은 Eq. (2)와 같다.
수식
고도각 모델은 고도각이 증가할수록 잡음의 분산을 나타내는 σi2이 작아지는 방식으로 가중값이 부여된다 (Kim 2015). Fig. 4는 고도각 기반 모델에 따른 잡음의 분산 변화를 나타낸 것으로 고도각이 증가함에 따라 분산이 급격히 감소하는 특징을 확인할 수 있다.
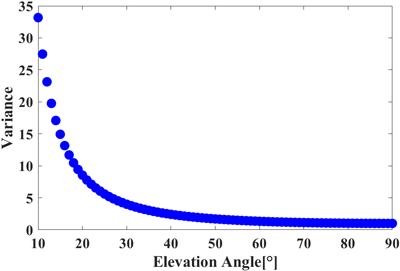
고도각 기반 가중값 모델은 계산 과정이 단순하고 구현이 용이하다는 장점이 있다. 그러나 2.1절에서 설명한 바와 같이, 스마트폰 GNSS에서는 고도각과 C/N0의 상관성이 일반 수신기보다 낮게 나타나며 높은 고도각에서도 신호 품질이 불안정하게 유지된다. 이로 인해 고도각 모델은 스마트폰의 신호 품질을 정확히 반영하지 못하는 한계가 있다.
C/N0 기반 가중값 모델은 Brunner et al. (1999)와 Li & Wu (2009) 등에 의해 도입된 확률적 모델로, 신호 품질을 직접 반영하여 코드의사거리 관측값의 잡음 수준을 설명한다. 본 연구에서는 Bahadur & Schön (2024)에 의해 스마트폰 GNSS에 맞도록 수정된 시그마 모델을 적용하였으며, Eq. (3)과 같다.
수식
여기서
C
는 주파수 및 위성 신호 별로 달라지는 분산 계수이다. 이 모델은 스마트폰의 신호 품질 특성을 고려하여 기준 C/N0 값을 40 dB-Hz로 설정하였다. Fig. 5는 시그마 모델에 따른 분산의 변화를 나타낸다. C/N0가 증가할수록 잡음의 분산을 나타내는
σ
2
i
이 감소하며 기준 C/N0에서 분산은 1로 수렴하게 된다.
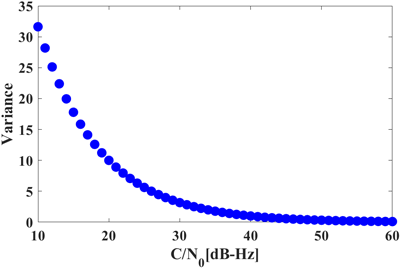
C/N0 기반 가중값 모델은 신호 품질을 반영하는 효과적인 방법으로 평가된다. 그러나 C/N0 값이 낮더라도 관측 잡음이 작은 경우가 발생할 수 있어 신호 품질을 정확하게 반영하지 못하는 한계를 가진다 (Hu et al. 2023). 따라서 C/N0 만을 단독 기준으로 신호 품질을 평가하는 것에는 한계가 있으며 관측값 자체의 특성을 반영할 수 있는 추가적인 고려가 필요하다.
이번 장에서는 스마트폰 GNSS 관측값의 특성과 신호 품질을 반영하는 새로운 가중값 모델을 제안한다. 4.1절에서는 코드의사거리 관측값 기반의 2차 다항식 곡선 접합 기법을 통해 관측 잡음 수준을 정량화 하는 방법을 다룬다. 이어서, 4.2절에서는 정량화된 관측 잡음 수준을 C/N0와 결합하여 최적의 가중값을 생성하는 방법을 제시한다.
스마트폰 코드의사거리 관측값의 잡음 수준은 2.2절에 설명한 바와 같이, 일반 수신기에 비해 약 10배 이상 크게 나타난다. 기존에는 반송파 위상과 코드의사거리 관측값을 이용하여 관측 잡음 수준을 측정하였으나 본 연구에서는 반송파 위상의 불연속성을 고려하여 코드의사거리 관측값만을 이용하였다. 코드의사거리는 Eq. (4)와 같이 구성된다.
수식
여기서 ρ는 위성과 수신기 간 기선 거리, δtr와 δts는 각각 수신기 시계 오차와 위성 시계 오차를 의미하며, δI와 δT는 대기권 오차, MP와 ε는 다중경로 오차와 관측 잡음을 나타낸다. 스마트폰은 다중경로 오차와 관측 잡음의 영향의 영향을 크게 받으며 두 요소를 명확히 구분하기 어렵다 (Mu et al. 2024). 본 연구에서는 다중경로 오차와 관측 잡음을 모두 잡음으로 간주하여 분석을 진행하였다.
코드의사거리 관측값에서 짧은 시간 동안 대기 오차는 일정하게 유지되며 시계 오차는 점진적으로 증가하는 경향이 있다. 따라서 수신기가 고정되어 있는 환경에서 코드의사거리 관측값의 변화는 위성 궤도와 잡음 수준에 영향을 받는다. 이러한 특성을 모델링하기 위해 슬라이딩 윈도우 기반 코드의사거리 2차 곡선 접합 기법을 적용하였다.
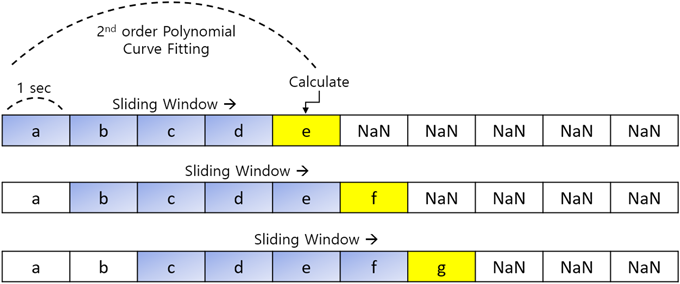
Fig. 6은 슬라이딩 윈도우 기반 코드의사거리 2차 다항식 곡선 접합 기법을 활용한 데이터 처리 과정을 보여준다. 각 슬라이딩 윈도우는 1초 간격으로 수집된 관측값을 포함하며 윈도우 크기는 5초로 설정하였다. 윈도우 내의 코드의사거리 관측값을 바탕으로 2차 다항식 곡선을 접합하여 관측값의 변화를 모델링하였다. 이후, 윈도우 내 마지막 관측값과 2차 곡선에 의해 추정된 값을 이용하여 잔차를 계산하였다.
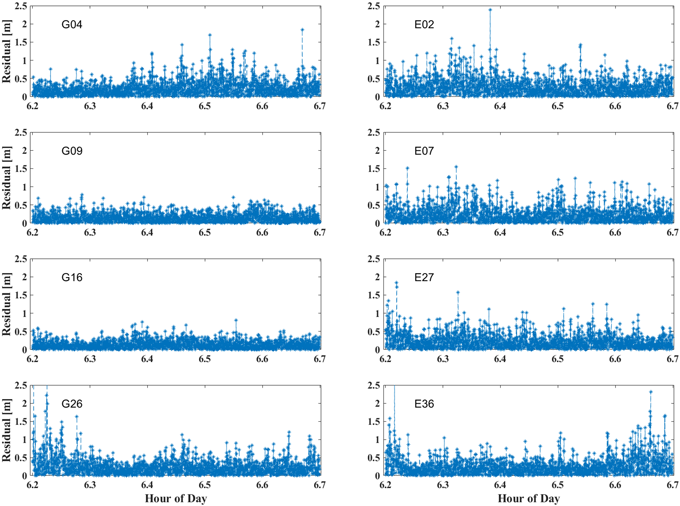
Fig. 7은 8개 위성의 코드의사거리 관측값에서 계산된 잔차를 나타낸다. 본 연구는 미국의 GPS와 유럽의 Galileo를 대상으로, 각각 L1신호와 E1 신호를 이용하였다. G09와 G16 위성은 전체 관측 시간 동안 일정한 수준의 잔차를 유지하여 신호 품질이 안정적인 것으로 평가되었다. 반면 G04, G26, E02 등의 위성에서는 특정 시간대에 잔차가 증가하였으며 이는 해당 시간대에 관측 잡음이 크게 증가했음을 의미한다. 이러한 측정 방법은 코드의사거리 관측값만을 이용하여 관측값의 잡음 수준을 정량화할 수 있으며 관측값의 품질 평가에 효과적으로 활용될 수 있다.
4.1절에서 도출한 관측 잡음 수준을 C/N0와 결합하여 가중값 모델을 설계하였다. C/N0은 신호품질을 나타내는 전통적인 지표로서 도심지와 개활지 같은 환경적 변화에 따라 변동하며 관측값의 신뢰도를 평가하는 데 중요한 역할을 한다.
본 연구에서는 C/N0와 관측 잡음을 각각 지수함수로 모델한 후, 이를 결합하는 새로운 가중값 모델을 제안한다. 해당 모델은 Eqs. (5, 6)과 같다.
수식
Eq. (5)는 신호의 품질을 반영하여, C/N0 값이 높을수록 관측값의 신뢰도가 증가함을 나타내며, Eq. (6)은 잔차가 클수록 관측 잡음이 크다는 것을 의미한다. 경험적 계수인 a, b, c는 스케일 팩터(scale factor)로 Eqs. (5, 6)에서 구한 가중치의 범위를 0과 1 사이의 값으로 설정하는 역할을 한다. 이는 스마트폰 기종 및 하드웨어 특성에 따라 조정되어야 하며 본 논문에서는 2.1절에 사용한 데이터를 기반으로 a, b, c를 각각 0.1, 0.004, 0.11로 설정하였다. 두 지표는 상호 보완적인 역할을 수행하며 관측값의 특성과 신호 품질을 반영한다.
Fig. 8은 이 연구에서 제안하는 가중값 모델의 결과를 시각적으로 나타낸다. 좌측 그래프는 Eqs. (5, 6)에 따른 분산을 나타내며, 우측 그래프는 두 모델을 가중치간 곱 연산하여 계산된 최종 가중값을 나타낸다. Colorbar는 C/N0 값을 나타내며 높은 C/N0 값은 붉은색, 낮은 C/N0 값은 파란색으로 표현하였다.
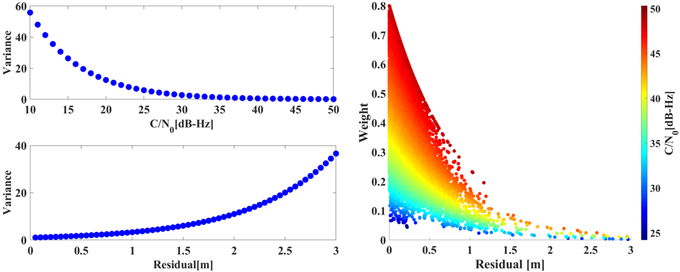
C/N0가 높고 관측 잡음이 작은 경우에는 해당 관측값에 높은 가중값을 부여하였고, 반대로 C/N0가 낮고 잡음 수준이 큰 경우에는 낮은 가중값을 부여하였다. C/N0가 높으면서 잡음 수준이 큰 경우나 그와 반대되는 상황에서는 두 지표가 상호 보완적인 역할을 수행함으로써 관측값의 품질을 정밀하게 반영할 수 있다.
본 연구에서는 Samsung Galaxy S21+를 사용하여 2024년 1월 22일, 2월 27일, 9월 9일 (DOY 022, 058, 253)에 인하대학교 농구장에서 30분간 검증 데이터를 수집하였다. 테스트 환경은 Fig. 9와 같으며, 기준 좌표는 (주)피피솔의 RTAP2U 수신기와 국토지리정보원에서 운영하는 Virtual Reference Station (VRS) 서비스를 통해 산출하였다.

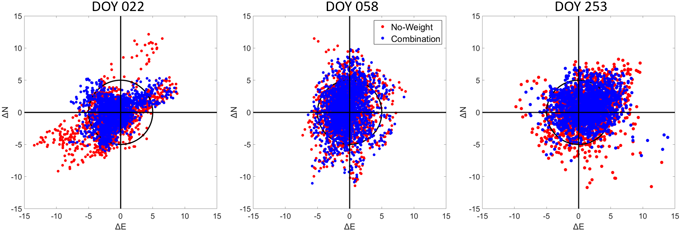
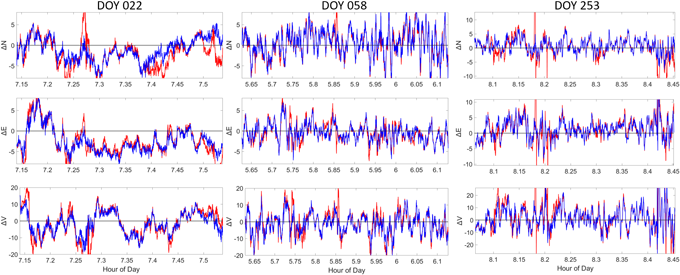
각 테스트의 측위 성능 평가는 Figs. 10과 11 그리고 Table 2와 같다. Fig. 10은 각 DOY 별로 산출된 수평 방향 오차이며, Fig. 11은 3차원 N, E, V 방향의 시계열 오차를 나타낸다. Figs. 10과 11의 단위는 m이며, 가중값을 적용하지 않은 경우는 붉은색으로, C/N0와 관측 잡음 수준 결합 가중값 모델을 적용한 경우는 파란색으로 표현하였다.
table
Table 2는 각 DOY별 테스트 결과로, 고도각 기반 가중값 모델(elevation), C/N0 기반 가중값 모델(C/N0) 그리고 본 연구에서 제안하는 가중값 모델(combination)을 적용하였을 때의 측위 정확도를 비교한 것이다. 정확도 평가를 위해 수평, 수직, 3차원 방향에 대한 RMSE와 RMSE 향상률을 확인하였다. 테스트 결과, Combination 모델을 적용했을 때 DOY 022에서는 수평과 수직 RMSE가 각각 약 40%와 32% 개선되었으며, DOY 058에서는 각각 약 10%와 20%, DOY 253에서는 약 33%와 23%의 RMSE 향상률을 보였다. 이는 C/N0과 관측 잡음을 결합한 Combination 모델이 스마트폰 측위에서 고도각, C/N0을 사용한 기존 모델보다 더 효과적임을 나타낸다.
본 연구에서는 스마트폰 GNSS의 위치 정확도 향상을 위해 C/N0와 코드의사거리 잔차를 결합하는 새로운 가중값 모델을 제안하였다. 모델의 개발을 위해 스마트폰 GNSS 관측값의 품질과 잡음을 분석하였고 기존에 제안된 가중값 모델을 검토하였다. 이를 통해 고도각 및 C/N0 기반 가중값 모델은 관측값 자체의 특성을 반영하지 않아 스마트폰 환경에서 신호 품질을 정확하게 반영하는 데 한계가 있음을 확인하였다.
본 연구는 관측값 자체의 특성을 반영하기 위해 슬라이딩 윈도우 기반의 코드의사거리 관측값을 2차 다항식 곡선으로 접합하고, 윈도우 내 마지막 관측값과 추정값의 차이를 이용하여 관측 잡음 수준을 정량화하였다. 이후, 정량화된 관측 잡음 수준과 C/N0을 결합함으로써 두 지표가 상호 보완적인 역할을 수행하는 가중값 모델을 개발하였다.
제안된 모델은 인하대학교 농구장에서 수행된 단독 측위 테스트를 통해 검증되었다. 테스트 결과, 제안된 가중값 모델은 수평과 수직 RMSE에서 각각 최대 40%, 32%의 개선 효과를 보였다. 이는 본 연구의 가중값 모델이 스마트폰 GNSS 관측값의 신뢰도를 보다 정밀하게 평가하고 기존 모델 대비 우수한 성능을 제공할 수 있음을 입증한다. 향후 연구에서는 다양한 환경에서 추가 테스트를 수행하여 모델의 보편성을 검증하고 난수신 및 동적 환경에서의 활용 가능성을 평가하여 더욱 정밀한 확률적 모델을 개발할 필요가 있다.
This research was supported by Korea Agency for Infrastructure Technology Advancement grant funded by the Ministry of Land, Infrastructure and Transport (RS-2022-00141819, Development of Advanced Technology for Absolute, Relative, and Continuous Complex Positioning to Acquire Ultra-precise Digital Land Information).
Conceptualization, J.L. and K.P.; methodology, J.L.; software, J.L.; validation, J.L., K.P. and M.K; formal analysis, J.L.; investigation, J.L.; resources, J.L. and B.P; data curation, J.L. and B.P; writing—original draft preparation, J.L.; writing—review and editing, J.L., K.P., B.P and M.K; visualization, J.L. and K.P; supervision, K.P and M.K.; project administration, K.P.; funding acquisition, K.P.
The authors declare no conflict of interest.
Bahadur, B. & Schön, S. 2024, Improving the stochastic model for code pseudorange observations from Android smartphones, GPS Solutions, 28, 148. https:// doi.org/10.1007/s10291-024-01690-y
Bisnath, S. & Aggrey, J. 2024, Current Limitations and Prospects for Smartphone GNSS Precise Positioning, Proceedings of the 2024 International Technical Meeting of The Institute of Navigation, Long Beach, California, January 23-25 2024, pp.1-24. https://doi. org/10.33012/2024.19560
Brunner, F., Hartinger, H., & Troyer, L. 1999, GPS signal diffraction modelling: the stochastic SIGMA-δ model, Journal of Geodesy, 73, 259-267. https://doi. org/10.1007/s001900050242
Fortunato, M., Ravanelli, M., & Mazzoni, A. 2019, Real-Time Geophysical Applications with Android GNSS Raw Measurements, Remote Sens., 11, 2113. https://doi. org/10.3390/rs11182113
Hu, J., Yi, D., & Bisnath, S. 2023, A comprehensive analysis of smartphone GNSS range errors in realistic environments, Sensors, 23,1631. https://doi.org/10.3390/s23031631
Håkansson, M. 2019, Characterization of GNSS observations from a Nexus 9 Android tablet, GPS Solutions, 23, 21. https://doi.org/10.1007/s10291-018-0818-7
Kim, H.-I. 2015, Improvement of the real-time positioning accuracy in urban canyons through development of a new weight model based on GNSS signal strength, PhD T hesis, Inha University.
Li, J. & Wu, M. 2009, The improvement of positioning accuracy with weighted least square based on SNR, Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, September 24-26 2009, pp.145-150. https://doi. org/10.1109/WICOM.2009.5302600
Li, Y., Cai, C., & Xu, Z. 2022, A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones, Sensors, 22, 2804. https://doi. org/10.3390/s22072804
Mu, H., Yu, X., Aragon-Angel, A., Wang, J., & Wu, Y. 2024, Real-time detection and correction of abnormal errors in GNSS observations on smartphones, Remote Sens., 16, 3117. https://doi.org/10.3390/rs16173117
Yun, J., Lim, C., & Park, B. 2022, Inherent Limitations of Smartphone GNSS Positioning and Effective Methods to Increase the Accuracy Utilizing Dual-Frequency Measurements, Sensors, 22, 9879. https://doi. org/10.3390/s22249879
Zangenehnejad, F. & Gao, Y. 2021, GNSS smartphones positioning: advances, challenges, opportunities, and future perspectives, Satell Navig, 2, 24. https://doi. org/10.1186/s43020-021-00054-y
Zangenehnejad, F. & Gao, Y. 2023, Stochastic Modeling of Smartphones GNSS Observations Using LS-VCE and Application to Samsung S20, Sensors, 23, 3478. https:// doi.org/10.3390/s23073478