Department of Electronic Engineering, Hanyang University, Seoul 04763, South Korea
†Corresponding Author: Sunwoo Kim, E-mail: remero@hanyang.ac.kr
Citation: Yang, D., Kang, J., Jeong, M., & Kim, S, 2024, RTT-Enabled Doppler Positioning in LEO-PNT Systems, Journal of Positioning, Navigation, and Timing, 13, 301-307.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 September, Volume 13, Issue 3, pages 301-307. https://doi.org/10.11003/JPNT.2024.13.3.301
Received on Aug 14, 2024, Revised on Aug 26, 2024, Accepted on Aug 27, 2024, Published on Sep 15, 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In this paper, we propose a round trip time (RTT)-enabled Doppler-based positioning method considering the low earth orbit (LEO) satellite visibility restriction. Doppler-based positioning typically requires visibility to at least eight satellites, which is often unfeasible due to the limited coverage of LEO satellites, as beamforming technique is applied to current LEO satellites. To solve this problem, we utilize the RTT measurements, assuming that a communication link exists between the user equipment (UE) and LEO satellites. We employ the Newton-Raphson method to estimate the UE position with RTT and Doppler measurements. We analyze the positioning performance of the considered framework via simulation, demonstrating its performance in 3D positioning errors under varying satellite numbers and measurement errors.
Doppler positioning, LEO-PNT, NTN, RTT positioning, satellite visibility
최근 low earth orbit-position, navigation and timing (LEO-PNT)은 기존 global navigation service system (GNSS)의 보완 및 대체제로 각광받고 있다 (Prol et al. 2022, Ferre et al. 2022, Stock et al. 2024). 기존 GNSS 대비 LEO-PNT의 장점은 다음과 같다. 먼저 low earth orbit (LEO) 위성은 global positioning service (GPS) 대비 약 10배 이상 낮은 600 km에서 2,000 km의 고도에 위치하기 때문에 보다 높은 C/N0를 보인다. 대표적으로 Ferre et al. (2022)는 시뮬레이션을 통하여 Starlink가 GPS 대비 실외에서 16.9 dB/Hz, 실내에서 6.2 dB/Hz의 C/N0 이득이 있음을 보였으며 이는 높은 신호획득 성능이 보장됨을 뜻한다. 다음으로 Starlink, Oneweb, Kuiper와 같은 다중 LEO 위성군을 모두 측위에 활용하게 될 경우 MEO 대비 약 2.5배 낮은 geometric delusion of precision (GDOP)를 가지며 이러한 낮은 GDOP는 LEO-PNT가 보다 정확한 측위 정확도를 달성할 수 있음을 의미한다 (Ferre et al. 2022, Prol et al. 2024).
이러한 장점에도 불구하고 현재 대다수의 LEO 위성은 통신목적 위성이며 측위를 위한 신호를 송신하지 않는다. 또한 현 시점의 Starlink, Oneweb, Kuiper와 같은 LEO 위성은 사기업이 소유하고 있으므로 신호구조가 공개되어 있지 않거나, 중심 주파수나 변조기법과 같은 일부만이 알려져 있다 (Humphreys et al. 2023, Kassas et al. 2024). 이에 따라 신호구조에 대한 정보 없이 얻을 수 있는 carrier phase와 도플러 천이에 기반한 측위 기법이 현재 주요 기술로 여겨지고 있으며 Khalife et al. (2021, 2022)는 신호 구조를 알 수 없는 LEO 위성신호에서 도플러 천이 및 carrier phase를 획득 및 추적한 바 있다. 특히 도플러 천이 기반 측위는 carrier phase 기반 측위와 다르게 송수신단 간 시각 오차에 영향받지 않으며 이는 원자시계 부재로 인해 시각 동기화에 어려움이 있는 LEO-PNT에 적합하다. 또한 약 7 km/s의 빠른 위성 속도로 인해 향상된 도플러 천이 활용성으로 인하여 보다 정확한 측위가 가능하다는 장점을 가지고 있다 (Khalife & Kassas 2019, Shi et al. 2023).
상기의 장점으로 인하여 LEO 위성 신호의 도플러 천이 기반 측위에 대한 다양한 연구가 이뤄지고 있다. Khalife & Kassas (2019)는 알지 못하는 통신 위성 신호를 활용하여 도플러 기반 측위를 실증한 바 있으며, Psiaki (2021)는 수치 실험을 통하여 다중 위성군을 사용한 도플러 기반 측위 기법의 유효성을 보였다. Guo et al. (2023)은 시뮬레이션을 통하여 도플러 측정값 오차가 0.01 m/s로 작을 때 미터 수준의 측위 오차가 달성 가능함을 보였으며, Wang et al. (2023)은 위성 궤도 오차를 고려한 도플러 기반 측위 기법을 제안하였고 실험을 통하여 오차 고려 시 약 70%의 성능 향상이 있음을 보였다. 그러나 도플러 기반 측위는 최소 8개 이상의 위성에 대한 가시성을 확보해야 하며 이는 현 LEO 위성의 빔 포밍을 통한 커버리지의 제약으로 인하여 불가능하다 (Psiaki 2021). McLemore & Psiaki (2022)는 이러한 빔 포밍 패턴을 고려했을 때 가시성 확보 가능한 위성은 최소 1개에서 최대 4개임을 수치실험을 통해 보인 바 있다.
위성 가시성 확보 문제를 해결하기 위해 도플러 천이와 inertial navigation system (INS)을 같이 활용하는 연구가 진행되고 있다 (McLemore & Psiaki 2022, Du et al. 2024). McLemore & Psiaki (2022)는 비행체용 inertial measurement unit (IMU) 센서 데이터와 적은 수의 LEO 위성으로부터 수신한 도플러 천이를 같이 활용한 extended Kalman filter (EKF) 기반 측위 기법을 제안하였으며, Du et al. (2024)은 차량용 INS와 Iridium 위성 신호의 도플러 천이를 활용한 federated Kalman filter (FKF) 기반 측위 기법을 제안 및 실증하였다. 그러나 이러한 고정밀의 차량 및 비행체용 INS는 휴대용 단말이나 internet of things (IoT)와 같은 전력 및 크기가 제한된 경우 탑재가 불가능하기 때문에 LEO 위성으로부터의 측정값만을 활용한 측위 기법이 요구된다.
본 논문은 위성 가시성 제약이 있는 상황에서 round trip time (RTT)와 도플러 천이를 용한 측위 기법을 제안한다. Nawaz et al. (2023)은 RTT-도플러 천이 기반 측위 기법을 이미 제시하였으나 단일 LEO 위성만을 고려하였다. 차세대 이동통신 시스템은 다중 위성 통신 신호 기반 정밀 측위를 고려하며 (Dureppagari et al. 2023), 우리가 아는 한 다중 LEO 위성 시나리오에서 RTT와 도플러 천이를 활용한 측위 기법 연구는 현재 존재하지 않는다. 제안 기법은 측위 대상인 단말과 LEO 위성과의 통신 상황 가정 하에 RTT 및 도플러 측정값을 다중 LEO 위성으로부터 측정한다. 측정값은 단말 위치와 비선형 함수로 표현됨에 따라 Newton-Raphson 기법을 사용하여 단말 위치를 추정한다. 성능 검증을 위한 시뮬레이션을 진행하였으며 위성수와 측정값 오차 별 측위 성능 오차를 분석한다.
본 논문의 구성은 다음과 같다. 2장에서 시스템 모델을 제시하고 3장에서 Newton-Raphson 기법을 사용한 RTT 및 도플러 천이 기반 측위 기법을 제시한다. 4장에서 수치실험 환경 제시와 위성수 및 측정값 잡음 별 측위 성능 분석을 진행하고, 마지막으로 5장에서 결론을 맺는다.
본 논문은 earth centered earth fixed (ECEF) 프레임을 따르며 고려하는 시나리오는 Fig. 1과 같다. 속도 $\mathbf{v}_{\ell} = \begin{bmatrix} v_{x,\ell} & v_{y,\ell} & v_{z,\ell} \end{bmatrix}^{\mathsf{T}}$로 움직이는 L개의 위성 $\mathbf{p}_{\ell} = \begin{bmatrix} x_{\ell} & y_{\ell} & z_{\ell} \end{bmatrix}^{\mathsf{T}}$로부터 위치를 알지 못하는 단말 $\mathbf{p}_{\mathrm{UE}} = \begin{bmatrix} x & y & z \end{bmatrix}^{\mathsf{T}}$가 RTT $τ_{RTT,l}$ 및 도플러 천이 $f_{D,l}$를 측정한다 (Nawaz et al. 2023). 측정 오차를 포함한 RTT 측정값을 통하여 오차를 포함한 $l^th$ 위성 간의 거리 $r_{RTT,l}$을 Eq. (1)과 같이 구할 수 있다.
$$r_{\text{RTT},\ell} = \frac{c T_{\text{RTT},\ell}}{2} = \| \mathbf{p}_{\text{UE}} – \mathbf{p}_{\ell} \| + c \delta_{\text{atmos},\ell} + c n_{\text{RTT},\ell}$$
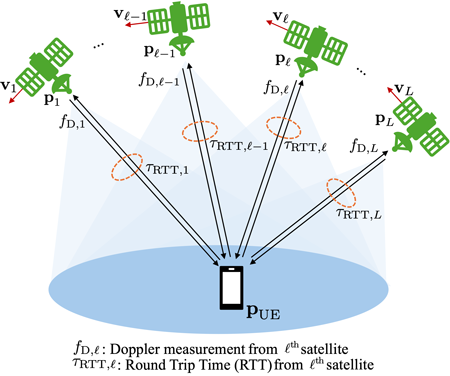
Fig. 1. Considered scenario with the NTN LEO satellites.
여기서 c는 자유공간에서의 전파 속도, $n_{\mathrm{RTT},\ell} \sim \mathcal{N}(0, \sigma^2_{\mathrm{RTT}\ell})$은 정규화된 RTT 측정 잡음이다. 본 논문에서 대류권과 이온층 지연을 포함하는 $\delta _{atmos,l}$는 보정 가능함을 가정한다 (Causa et al. 2017).
도플러 천이 측정값은 신호의 반송파 주파수 $f_c$에 따른 파장 $\lambda _c$를 통해 거리 변화율로 변환할 수 있다. 측정 오차를 포함한 $l^{th}$ 위성과의 거리 변화율 $r_{D,l}$은 Eq. (2)와 같다.
$$r_{D,\ell} = -\lambda_c f_{D,\ell} = \frac{(\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}})^\top (\mathbf{v}_{\ell} – \mathbf{v}_{\text{UE}})}{\| \mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}} \|} + c \dot{\delta}_{\text{clk}} + c \dot{\delta}_{\text{clk},\ell} + \dot{\delta}_{\text{atmos},\ell} + \lambda_c n_{D,\ell}$$
여기서 $\mathbf{v}_{UE} \in \mathbb{R}^3$는 단말의 도플러 천이 측정 시점에서의 속도, $n_{D,\ell} \sim \mathcal{N}(0, \sigma_{D,\ell}^2)$은 도플러 천이 측정 오차, $\dot{\delta}_{clk}$, $\dot{\delta}_{clk,l}$는 각각 단말 및 $l^{th}$ 위성의 clock drift이며 $\dot{\delta}_{atmos}$는 대기 지연 변화율이다. 이 때, $\dot{\delta}_{atmos}$는 측정 잡음 대비 작아 무시 가능함을 가정하며 위성의 위치, 속도, 시각 정보는 통신 링크로 얻을 수 있음을 가정하므로 $\dot{\delta}_{clk,l}$는 보정 가능하다.
모든 L개 위성에 대한 RTT 기반 거리와 도플러 기반 거리 변화율 측정값 벡터 $\mathbf{r} = [r_{\text{RTT},1} \cdots r_{\text{RTT},L} \; r_{\text{D},1} \cdots r_{\text{D},L}] \in \mathbb{R}^{2L}$는 Eq. (3)과 같다.
$$\mathbf{r} = \begin{bmatrix} \boldsymbol{\mu}_{\text{RTT}} \\ \boldsymbol{\mu}_{D} \end{bmatrix} + \mathbf{n},$$
여기서 $\boldsymbol{\mu}_{\text{RTT}} = \begin{bmatrix} \mu_{\text{RTT},1} & \cdots & \mu_{\text{RTT},L} \end{bmatrix}^{\top} \in \mathbb{R}^{L}$, $\boldsymbol{\mu}_{\text{D}} = \begin{bmatrix} \mu_{\text{D},1} & \cdots & \mu_{\text{D},L} \end{bmatrix}^{\top} \in \mathbb{R}^{L}$는 각 모든 L개 위성에 대한 Eq. (1)의 RTT 기반 거리 벡터인 $\mathbf{r}_{RTT} = \left[ r_{RTT,1} \cdots r_{RTT,L} \right]^{\mathsf{T}} \in \mathbb{R}^L$와 Eq. (2)의 도플러 기반 거리 변화율 벡터 $\mathbf{r}_{D} = \left[ r_{D,1} \cdots r_{D,L} \right]^{\mathsf{T}} \in \mathbb{R}^L$의 오차를 포함하지 않는 벡터다. $\mathbf{n} = \left[ n_{RTT,1} \cdots n_{RTT,L} \; n_{D,1} \cdots n_{D,L} \right]^{\mathsf{T}} \sim \mathcal{N}(0, \mathbf{\Sigma}) \in \mathbb{R}^{2L}$는 측정 오차 벡터로 모든 성분 간 독립을 가정하며 이에 따라 오차 공분산 행렬 $\mathbf{\Sigma} \in \mathbb{R}^{2L \times 2L}$는 $\mathbf{\Sigma} = \operatorname{diag}(\sigma_{RTT,1}^2, \cdots, \sigma_{RTT,L}^2, \sigma_{D,1}^2, \cdots, \sigma_{D,L}^2)$이다. 여기서 diag(⋅)는 ⋅ 을 대각 성분으로 하는 대각행렬이다.
Eq. (3)에 따라 단말 위치, 속도, clock drift 추정값 $\hat{\mathbf{p}}_{\text{UE}}$, $\hat{\mathbf{v}}_{\text{UE}}$, $\hat{\delta}_{\text{clk}}$를 위한 목적 함수는 Eq. (4)와 같이 정의된다.
$$\hat{\mathbf{p}}_{\mathrm{UE}},\ \hat{\mathbf{v}}_{\mathrm{UE}},\ \hat{\delta}_{\mathrm{clk}}
= \underset{\mathbf{p}_{\mathrm{UE}},\ \mathbf{v}_{\mathrm{UE}},\ \delta_{\mathrm{clk}}}
{\mathrm{arg}\ \min}
(\mathbf{r} – \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\mathbf{r} – \boldsymbol{\mu})
$$
여기서 $\boldsymbol{\mu} = \begin{bmatrix} \boldsymbol{\mu}_{\text{RTT}}^\top & \boldsymbol{\mu}_{\text{D}}^\top \end{bmatrix}^\top \in \mathbb{R}^{2L}$은 모든 측정값의 오차를 제외한 벡터이다.
Eq. (4)의 해를 구하기 위하여 Newton-Raphson 기법을 사용한다 (Ypma 1995, Shi et al 2023). 알지 못하는 단말 위치, 속도, clock drift를 $\mathbf{x}_{\text{UE}} = \begin{bmatrix} \mathbf{p}_{\text{UE}}^\top & \mathbf{v}_{\text{UE}}^\top & \delta_{\text{clk}} \end{bmatrix}^\top \in \mathbb{R}^7$라 할 때, $\mathbf{x}_{UE}$와 μ 간의 관계가 비선형 이므로 테일러 1차 근사를 통한 선형화를 진행한다. k번째 값 $\mathbf{x}_{\text{UE}, k} = \begin{bmatrix} \mathbf{p}_{\text{UE}, k}^\top & \mathbf{v}_{\text{UE}, k}^\top & \delta_{\text{clk}, k} \end{bmatrix}^\top$에 대하여 $\mu$는 Eq. (5)와 같다.
$$\boldsymbol{\mu} \approx \boldsymbol{\mu}_k + \mathbf{J}_k \Delta \mathbf{x}_{\text{UE}, k}$$
여기서 $\boldsymbol{\mu}_k \in \mathbb{R}^{2L}$는 오차를 포함하지 않는 측정값 벡터 $\boldsymbol{\mu}$의 $\mathbf{x}_{\text{UE,k}}$ 시점의 거리 및 속도변화율 벡터이며 $\Delta \mathbf{x}_{\text{UE}, k} = \mathbf{x}_{\text{UE}} – \mathbf{x}_{\text{UE}, k}$는 k번째 $\mathbf{x}_{\text{UE}, k}$에 대한 오차 보정 벡터이다. $\boldsymbol{\mu}$의 $\mathbf{x}_{\text{UE}, k}$에 대한 자코비안 행렬 $\mathbf{J}_k \in \mathbb{R}^{2L×7}$는 Eq. (6)과 같다.
$$\mathbf{J}_k = \frac{\partial \boldsymbol{\mu}}{\partial \mathbf{x}_{\text{UE}, k}} = \begin{bmatrix}
\frac{\partial \boldsymbol{\mu}_{\text{RTT}, 1}^\top}{\partial \mathbf{p}_{\text{UE}, k}} & 0 & 0 \\
\vdots & \vdots & \vdots \\
\frac{\partial \boldsymbol{\mu}_{\text{RTT}, L}^\top}{\partial \mathbf{p}_{\text{UE}, k}} & 0 & 0 \\
\frac{\partial \boldsymbol{\mu}_{\text{D}, 1}^\top}{\partial \mathbf{p}_{\text{UE}, k}} & \frac{\partial \boldsymbol{\mu}_{\text{D}, 1}^\top}{\partial \mathbf{v}_{\text{UE}, k}} & \frac{\partial \boldsymbol{\mu}_{\text{D}, 1}^\top}{\partial \delta_{\text{clk}, k}} \\
\vdots & \vdots & \vdots \\
\frac{\partial \boldsymbol{\mu}_{\text{D}, L}^\top}{\partial \mathbf{p}_{\text{UE}, k}} & \frac{\partial \boldsymbol{\mu}_{\text{D}, L}^\top}{\partial \mathbf{v}_{\text{UE}, k}} & \frac{\partial \boldsymbol{\mu}_{\text{D}, L}^\top}{\partial \delta_{\text{clk}, k}}
\end{bmatrix}$$
여기서
$$\Delta \mathbf{x}_{\text{UE}, k} = \mathbf{x}_{\text{UE}} – \mathbf{x}_{\text{UE}, k}$$
$$\frac{\partial \boldsymbol{\mu}_{\text{RTT}, \ell}}{\partial \mathbf{p}_{\text{UE}, k}} = \frac{\mathbf{p}_{\text{UE}, k} – \mathbf{p}_{\ell}}{\|\mathbf{p}_{\text{UE}, k} – \mathbf{p}_{\ell}\|}$$
$$\frac{\partial \boldsymbol{\mu}_{\text{D}, \ell}}{\partial \mathbf{p}_{\text{UE}, k}} = \frac{1}{\|\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}, k}\|} \left( \frac{(\mathbf{v}_{\ell} – \mathbf{v}_{\text{UE}, k})^\top (\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}, k})}{\|\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}, k}\|^2} (\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}, k}) – (\mathbf{v}_{\ell} – \mathbf{v}_{\text{UE}, k}) \right)$$
그리고
$$\frac{\partial \boldsymbol{\mu}_{\text{D}, \ell}}{\partial \mathbf{v}_{\text{UE}, k}} = \frac{\mathbf{p}_{\text{UE}, k} – \mathbf{p}_{\ell}}{\|\mathbf{p}_{\ell} – \mathbf{p}_{\text{UE}, k}\|}$$
이다. 따라서 k+1번째 값 $\mathbf{x}_{\text{UE},k+1}$은 k번째 값 $\mathbf{x}_{\text{UE},k}$를 통하여 Eq. (11)을 얻을 수 있다.
$$\mathbf{x}_{\mathrm{UE},k+1} = \mathbf{x}_{\mathrm{UE},k} + \Delta \mathbf{x}_{\mathrm{UE},k}$$
이때 $\Delta \mathbf{x}_{\mathrm{UE},k}$는 Eq. (12)와 같다.
$$\Delta \mathbf{x}_{\mathrm{UE},k} = \left( \mathbf{J}_k^{\top} \mathbf{\Sigma}^{-1} \mathbf{J}_k \right)^{-1} \mathbf{J}_k^{\top} \mathbf{\Sigma}^{-1} (\mathbf{r} – \boldsymbol{\mu}_k)$$
초기값 $\Delta \mathbf{x}_{\mathrm{UE},0}$가 주어질 때 Eqs. (11, 12)의 업데이트 과정을 수렴 기준값 $\gamma$에 대하여 $\| \Delta \mathbf{x}_{\mathrm{UE},k} \| < \gamma$가 만족할 때까지 반복하며, 만약 이를 만족한다면 측정값이 충분히 수렴했다 판단하고 이를 종료한다. Table 1은 제안 기법의 의사 코드이다.
Table 1. Newton-Raphson method for RTT-Doppler positioning.
| Algorithm 1: Newton-Raphson method for RTT-Doppler positioning | |
|---|---|
| Input: $\mathbf{x}_{\mathrm{UE},0}$, $\mathbf{\Sigma}^{-1}$, $\mathbf{r}$, $\gamma$ | |
| Output: $\hat{\mathbf{x}}_{\mathrm{UE}}$ | |
| 1. Initialize $k$ as 0 | |
| while $k = 0$ or $\|\Delta \mathbf{x}_{\mathrm{UE},k}\| > \gamma$ do | |
| 2. $\Delta \mathbf{x}_{\mathrm{UE},k} \leftarrow \left(\mathbf{J}_k^{\top} \mathbf{Q}^{-1} \mathbf{J}_k\right)^{-1} \mathbf{J}_k^{\top} \mathbf{\Sigma}^{-1} (\mathbf{r} – \boldsymbol{\mu})$ | |
| 3. $\mathbf{x}_{\mathrm{UE},k+1} \leftarrow \mathbf{x}_{\mathrm{UE},k} + \Delta \mathbf{x}_{\mathrm{UE},k}$ | |
| 4. $k \leftarrow k + 1$ | |
| end | |
| 5. $\hat{\mathbf{x}}_{\mathrm{UE}} \leftarrow \mathbf{x}_{\mathrm{UE},k}$ | |
시뮬레이션을 위해 고려한 단말 및 LEO 위성의 위치는 다음과 같다. $\mathbf{p}_{\mathrm{UE}} = \begin{bmatrix} -3,043 & 4,031 & 3,883 \end{bmatrix}^{\top}$ km에 위치한 단말을 기준으로 고도각 10° 이하를 제외한 스타링크의 two line element (TLE) file로 LEO 위성의 위치 및 속도 정보를 얻었으며 계산의 편의성을 위하여 정지한 단말을 가정한다. 위성 가시성의 제약을 고려하기 위하여 단말 $\mathbf{p}_{\mathrm{UE}}$와 가장 근접한 $\begin{bmatrix} -3,043 & 4,031 & 3,883 \end{bmatrix}^{\top}$ km의 LEO 위성과 위성간 거리가 최대 6,371 km인 위성 중 L개의 위성을 선택하였다. 이 때, 위성간 거리 및 위성의 수는 LEO 위성간 통신 환경을 고려하여 측위 시뮬레이션을 진행한 Hashim et al. (2022)와 Dureppagari et al. (2023)에 기반하여 위성 수 L을 3에서 7로 설정하였다. Fig. 2는 위성 가시성 제약을 고려한 L=7개의 LEO 위성 및 단말 위치 분포 및 TLE file에 기반한 전체 추적 궤도를 나타낸다.
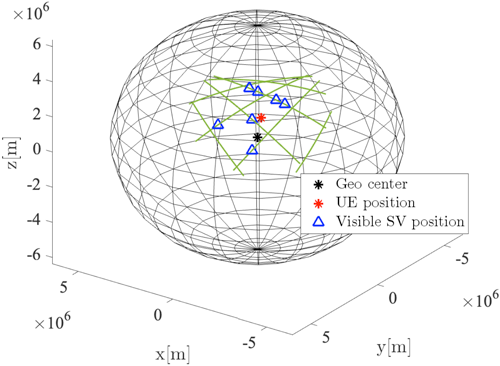
Fig. 2. Visible satellites in the restricted satellite visibility scenario.
신호의 반송파 주파수 $f_c$는 2 GHz로 이에 따라 파장은 $\lambda _c$는 0.15 m이다. RTT와 도플러 천이의 측정값 오차의 표준 편차는 Nawaz et al. (2023)이 고려한 범위 내에서 설정하였다. 따라서 RTT의 측정값 오차의 표준편차 $σ_{RTT,l}$는 0.01 μs에서 0.05 μs, 도플러 천이 측정값 오차의 표준편차 $σ_{D,l}$는 1 Hz에서 5 Hz로 하였으며 모든 l∈{1,…,L}에 대하여 동일하게 설정하였다. 또한 Newton-Raphson 기법의 수렴 기준값 γ는 0.001로 설정하였으며 수치 실험은 각 오차 표준편차 및 위성 수 별 10^4번 반복하여 진행하였다. 또한 측위 오차는 3차원 위치좌표에 대한 root mean squared error (RMSE)로 각 샘플 별 $\| \mathbf{p}_{\mathrm{UE}} – \hat{\mathbf{p}}_{\mathrm{UE}} \|$의 평균으로 계산하였다.
먼저, 도플러 천이 측정 오차 증가만을 고려했을 때의 측위 RMSE 경향을 확인하기 위한 시뮬레이션을 진행을 하였으며 결과는 Figs. 3, 4와 같다. RTT 측정 오차의 표준 편차 $σ_{RTT}$는 Fig. 3에서 0.05 μs, Fig. 4에서 0.005 μs로 설정하였다. Fig. 3의 결과를 볼 때 측위 RMSE는 RTT 표준 편차가 증가함에 따라 증가하나, 증가폭이 감소하는 경향을 보였다. 특히 $σ_D$= 2 Hz 이후부터 모든 비교 위성 수에 대한 측위 RMSE 증가 경향이 큰 폭으로 감소하였으며, 고려 위성 수 중 가장 작은 값인 L=3을 제외한 나머지 위성 수에 대한 측위 RMSE는 $σ_D$= 1 Hz 이후 큰 변동이 없음을 확인하였다. 위성 수 증가에 따른 측위 RMSE 감소는 L=3과 L=4를 비교했을 때, 29.32 m 감소하였으며 L=4 이후의 감소폭은 5 m 이하를 보였다. 이를 Fig. 4와 비교할 때 RTT 측정오차가 0.005 μs로 상대적으로 작은 경우 도플러 천이 오차 증가에 따른 측위 성능 영향이 미비함을 확인하였다.
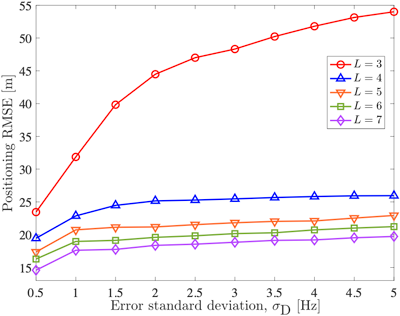
Fig. 3. Position RMSE on the number of satellites considering Doppler measurement error with fixed RTT measurement error (σRTT = 0.05 μs).
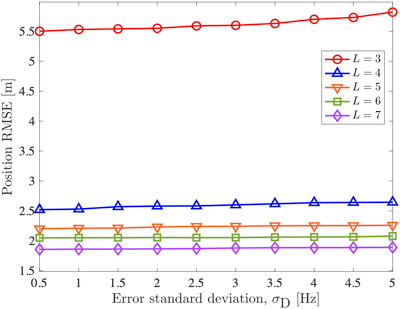
Fig. 4. Position RMSE on the number of satellites considering Doppler measurement error with fixed RTT measurement error (σRTT = 0.005 μs).
다음으로 RTT 측정 오차 증가만을 고려했을 때의 측위 RMSE 경향을 확인하기 위한 시뮬레이션을 진행을 하였으며 결과는 Figs. 5, 6과 같다. 도플러 측정 오차의 표준 편차 $σ_D$는 Fig. 5에서 5 Hz, Fig. 6에서 0.5 Hz로 설정하였다. Fig. 5의 결과를 볼 때 모든 고려 위성 수에 대한 측위 RMSE는 선형적으로 증가하였으며 그 경향성은 L=3일 때 가장 급격하게 증가하였다. 도플러 측정 오차 증가 만을 고려한 Fig. 3의 결과와 비교할 때, L=3의 경우 가장 큰 증가 경향을 보이는 것은 동일했으나, 도플러 천이와 다르게 RTT 오차 증가에 따른 측위 RMSE 경향성은 선형적으로 유지되었다. 위성 수 증가에 따른 측위 RMSE 감소 역시 Fig. 3의 결과와 유사하게 L이 3에서 4로 증가할 때 가장 컸으며, 5 이상의 경우 5 m 이하의 감소폭을 보였다. 또한 도플러 측정 오차의 표준편차가 0.5 Hz로 상대적으로 작은 Fig. 6과 비교할 때, 위성 수 증가에 따른 오차 감소 비율이 Fig. 6의 경우가 상대적으로 줄어든 것을 확인하였다. 이러한 시뮬레이션 결과에 따라 고려한 오차 표준 편차 범위에서 RTT 오차 증가에 따른 측위 성능 감소가 도플러 천이의 경우보다 크다고 판단하였다.
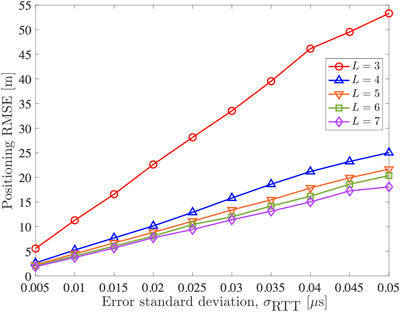
Fig. 5. Position RMSE on the number of satellites considering RTT measurement error with fixed Doppler measurement error (σD = 5 Hz).
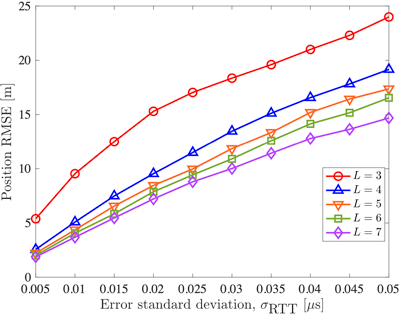
Fig. 6. Position RMSE on the number of satellites considering RTT measurement error with fixed Doppler measurement error (σD = 0.5 Hz).
마지막으로 위성 수 증가에 따른 위치 오차 $\| \mathbf{p}_{\mathrm{UE}} – \hat{\mathbf{p}}_{\mathrm{UE}} \|$의 분포를 확인하기 위한 시뮬레이션을 진행하였으며 그 결과는 Fig. 7과 같다. 이 때 각 측정값 별 오차 표준편차는 $σ_{RTT}$=0.05 μs, $σ_D$=5 Hz로 설정하였다. Fig. 7의 박스 상하단 경계는 각 오차 분포의 75, 25%를 나타내며, 붉은 선은 중앙값, 검은 실선은 나머지 값의 분포를 보여준다. L이 3에서의 경우 중앙값은 46.08, 24.28, 21.58, 18.14, 17.24 m를 보였다. L=4부터 오차의 전체 분포와 중앙값이 큰 폭으로 감소하였으며, 그 이후부터 감소폭이 크게 줄어든 것을 확인하였다.
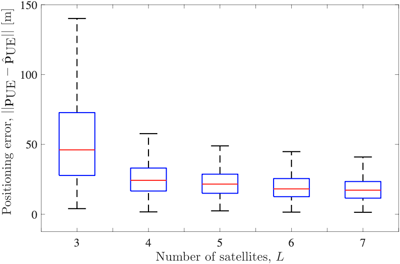
Fig. 7. Box plot of position errors in different number of satellites (σD = 5 Hz, σRTT = 0.05 μs).
본 논문은 LEO 위성 가시성에 제약이 있는 상황에서 RTT와 도플러 천이를 활용한 측위 기법을 제안하였다. 제안 기법은 LEO 위성과의 통신 링크가 보장된 상황에서 RTT와 도플러 천이 측정값을 같이 활용하여 Newton-Raphson 기법을 통해 단말의 위치를 추정하였다. 시뮬레이션을 통하여 위성 수에 따른 측위 성능 분석을 진행했으며 위성 수가 3에서 4로 증가하는 경우 가장 큰 폭으로 위치 RMSE가 감소하는 것을 확인했다. 특히 σ_RTT=0.05 μs,σ_D=5 Hz의 경우 위성 수가 3에서 4로 증가할 때 그 이상의 위성 수 증가 대비 약 5배인 29.32 m의 위치 RMSE 감소를 보였다. 향후 위성 가시성 제약을 고려한 이동 단말을 실시간으로 추적하는 새로운 측위 기법 연구가 필요하다.
이 연구 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임 (No. NRF-2023R1A2C3002890).
Conceptualization, D. Yang, J. Kang and M. Jeong; software, D. Yang and J. Kang; validation, D. Yang, J. Kang and M. Jeong; formal analysis, D. Yang, J. Kang, M. Jeong and S. Kim; data curation, D. Yang, J. Kang, M. Jeong and S. Kim; writing—original draft preparation, D. Yang; writing—review and editing, D. Yang, J. Kang, M. Jeong and S. Kim; visualization, D. Yang, J. Kang, M. Jeong and S. Kim; supervision, S. Kim; project administration, S. Kim; funding acquisition, S. Kim.
The authors declare no conflict of interest.
Causa, F., Renga, A., & Grassi, M. 2017, Ionosphere-gradient based filtering approach for precise relative navigation in LEO, In 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), 21-23 June 2017, Padua, Italy, pp.56-61. https://doi.org/10.1109/MetroAeroSpace.2017.7999538
Du, Y., Qin, H., & Zhao, C. 2024, LEO satellites/INS integrated positioning framework considering orbit errors based on FKF, IEEE Transactions on Instrumentation and Measurement, 73, 5501714. https://doi.org/10.1109/TIM.2024.3369693
Dureppagari, H. K., Saha, C., Dhillon, H. S., &. Buehrer, R. M. 2023, NTN-based 6G localization: Vision, role of LEOs, and open problems, IEEE Wireless Communications Magazine, 30, 44-51. https://doi.org/10.1109/MWC.007.2300224
Ferre, R. M., Lohan, E. S., Kuusniemi, H., Praks, J., Kaasalainen, S., et al. 2022, Is LEO-based positioning with mega-constellations the answer for future equal access localization?, IEEE Communications Magazine, 60, 40-46. https://doi.org/10.1109/MCOM.001.2100841
Guo, F., Yang, Y., Ma, F., Zhu, Y., Liu, H., et al. 2023. Instantaneous velocity determination and positioning using Doppler shift from a LEO constellation. Satellite Navigation, 4, 9. https://doi.org/10.1186/s43020-023-00098-2
Hashim, I. S. M., Al-Hourani, A., & Ristic, B. 2022, Satellite localization of IoT devices using signal strength and Doppler measurements, IEEE Wireless Communications Letters, 11, 1910-1914. https://doi.org/10.1109/LWC.2022.3187065
Humphreys, T. E., Iannucci, P. A., Komodromos, Z. M., & Graff, A. M. 2023, Signal structure of the Starlink Ku-band downlink, IEEE Transactions on Aerospace and Electronic Systems, 59, 6016-6030. https://doi.org/10.1109/TAES.2023.326810
Kassas, Z. M., Khairallah, N., & Kozhaya, S. 2024, Ad astra: Simultaneous tracking and navigation with megaconstellation LEO satellites, IEEE Aerospace and Electronic Systems Magazine (Early Access), 1-19. https://doi.org/10.1109/MAES.2023.3267440
Khalife, J. J. & Kassas, Z. M. 2019, Receiver design for Doppler positioning with LEO satellites, In ICASSP 2019 – 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 12-17 May 2019, Brighton, UK, pp.5506-5510. https://doi.org/10.1109/ICASSP.2019.8682554
Khalife, J., Neinavaie, M., & Kassas, Z. M. 2021, Blind Doppler tracking from OFDM signals transmitted by broadband LEO satellites, In 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), 25-28 April 2021, Helsinki, Finland, pp.1-5. https://doi.org/10.1109/VTC2021-Spring51267.2021.9448678
Khalife, J., Neinavaie, M., & Kassas, Z. M. 2022, The first carrier phase tracking and positioning results with Starlink LEO satellite signals, IEEE Transactions on Aerospace and Electronic Systems, 58, 1487-1491. https://doi.org/10.1109/TAES.2021.3113880
McLemore, B. & Psiaki, M. L. 2022, Navigation using Doppler shift from LEO constellations and INS data, IEEE Transactions on Aerospace and Electronic Systems, 58, 4295-4314. https://doi.org/10.1109/TAES.2022.3162772
Nawaz, S. J., Cianca, E., Rossi, T., & De Sanctis, M. 2023, Round Trip Time (RTT) and Doppler Measurements for IoRT Localization by a Single-Satellite, IEEE Communications Letters, 28, 528-532. https://doi.org/10.1109/LCOMM.2023.3348156
Prol, F. S., Ferre, R. M., Saleem, Z., Välisuo, P., Pinell, C., et al. 2022, Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities, IEEE Access, 10, 83971-84002. https://doi.org/10.1109/ACCESS.2022.3194050
Prol, F. S., Bhuiyan, M. Z. H., Kaasalainen, S., Lohan, E. S., Praks, J., et al. 2024, Simulations of Dedicated LEO-PNT Systems for Precise Point Positioning: Methodology, Parameter Analysis, and Accuracy Evaluation, IEEE Transactions on Aerospace and Electronic Systems (Early Access). https://doi.org/10.1109/TAES.2024.3404909
Psiaki, M. L. 2021, Navigation using carrier Doppler shift from a LEO constellation: TRANSIT on steroids, Navigation, 68, 621-641. https://doi.org/10.1002/navi.438
Shi, C., Zhang, Y., & Li, Z. 2023, Revisiting Doppler positioning performance with LEO satellites, GPS Solutions, 27, 126. https://doi.org/10.1007/s10291-023-01466-w
Stock, W., Schwarz, R. T., Hofmann, C. A., & Knopp, A. 2024, Survey on Opportunistic PNT With Signals from LEO Communication Satellites, IEEE Communications Surveys & Tutorials. https://doi.org/10.1109/COMST.2024.3406990
Wang, D., Qin H., & Huang, Z. 2023, Doppler Positioning of LEO Satellites Based on Orbit Error Compensation and Weighting, IEEE Transactions on Instrumentation and Measurement, 72, 5502911. https://doi.org/10.1109/TIM.2023.3286001
Ypma, T. J. 1995, Historical development of the Newton–Raphson method, SIAM review, 37, 531-551. http://www.jstor.org/stable/2132904