1Department of IT Engineering, Kyungil University, Gyeongsan 38428, Korea
2Department of Mechanical Automotive Engineering, Kyungil University, Gyeongsan 38428, Korea and NavIn Labs Co., Ltd. Daegu 42284, Korea
3Mobility UX Section, Electronics and Telecommunications Research Institute, Daejeon 34129, Korea
†Corresponding Author: Seong Yun Cho / JaeJun Yoo, E-mail: sycho@kiu.kr / jjryu@etri.re.kr
Citation: Kwon, J.U., Cho, S.Y., Yoo, J.J., & Seo, S.H., 2024, Adaptive Sensor/Heterogeneous Infrastructure Integrated Pedestrian Navigation Technology using Rényi Divergence-based Outlier Detection, Journal of Positioning, Navigation, and Timing, 13, 289-299.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 September, Volume 13, Issue 3, pages 289-299. https://doi.org/10.11003/JPNT.2024.13.3.289
Received on Aug 10, 2024, Revised on Aug 27, 2024, Accepted on Aug 29, 2024, Published on Sep 15, 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In the Pedestrian Dead Reckoning (PDR)/Global Positioning System (GPS)/Wi-Fi-integrated navigation system for indoor/outdoor continuous positioning of pedestrians, the process of detecting outliers in measurements is very important. When accurate location information from measurements is used, reliable correction data can be generated during the fusion filtering process. However, abnormal measurements may occur in certain situations, such as indoor/outdoor transitions, which can degrade filter performance and lead to significant errors in the estimated position. To address this issue, this paper proposes a method for detecting outliers in measurements based on Rényi Divergence (RD). When the deviation of the RD value is large, the measurements are considered outliers, and positioning is performed using only pure PDR. Based on experiments conducted with real data, it was confirmed that outliers were effectively detected for abnormal measurements, leading to an improvement in the performance of pedestrian navigation.
pedestrian navigation, PDR, Wi-Fi fingerprinting, Rényi divergence, outlier detection
최근 몇 년간 스마트폰 기술의 지속적인 발전과 광범위한 확산은 일상생활의 다양한 영역에서 편의성과 효율성을 크게 향상시켰다. 특히, 스마트폰의 유비쿼터스 컴퓨팅 환경과 다양한 센서의 통합은 사용자가 위치기반서비스를 더욱 효과적으로 활용할 수 있는 기반을 마련하였다. 이러한 발전은 위치기반서비스의 적용 범위를 크게 확장시켰으며, 내비게이션, 소셜 네트워킹, 물류관리, 공공 보안 등 다양한 분야에서 점차 보편화되고 있다. 위치기반서비스에 대한 신뢰성을 확보하기 위해서는 정확한 위치정보가 필수적이다. 실외 환경에서는 위성항법시스템인 Global Positioning System (GPS) 기술을 통해 위치정보를 획득할 수 있다. GPS는 Open-sky 환경에서 보행자 항법을 위한 정확한 측위 정보를 제공한다. 그러나 실내 공간과 같은 Non-line-of-sight (NLOS) 환경에서는 건물 외벽 및 다양한 구조물에 의한 다중 경로 문제로 인해 위치의 품질이 급격히 저하된다.
실내 측위 기술은 주로 Wi-Fi, Bluetooth Low Energy (BLE), Ultra-Wideband (UWB), Radio Frequency Identification (RFID)와 같은 무선 통신 정보를 사용한다 (Leitch et al. 2023). 이 중 공용 네트워크 인프라인 Wi-Fi Access Point (AP)는 거의 모든 실내 공간에 존재하기 때문에 실내 위치 서비스를 위한 다양한 응용 가능성을 제공한다. 따라서 Wi-Fi는 저렴한 비용과 높은 가용성으로 인해 실내 측위 기술에서 가장 선호되는 무선 인프라로 사용되고 있다.
실내 환경에서 Wi-Fi의 Received Signal Strength Indicator (RSSI) 정보를 이용한 측위 기술은 모델 기반 방법과 전자지문 기반 방법으로 분류할 수 있다 (Ma & Shi 2023). 모델 기반 측위 방법은 수신 장치와 AP 간의 거리 및 신호 전파 (Propagation) 모델을 활용하여 사용자의 위치를 추정하는 기술이다. 그러나 이 방법은 AP의 위치를 필요로 하며, 실제 환경에서 무선 신호의 전파 모델이 복잡하기 때문에 신뢰할 수 있는 측위 결과를 제공하기 어렵다 (Kwon & Cho 2021). 이와 달리 전자지문 기반 측위 방법은 확률론적 모델링에 기반한 기술로, 수신 장치가 측정한 RSSI 정보와 사전 구축된 데이터베이스 내의 RSSI 정보 간의 매칭 알고리즘을 통해 위치를 추정한다. 이 방법은 NLOS 영향을 받지 않으며, 환경 특성을 반영한 실제 RSSI 값을 사용하기 때문에 다중 경로 환경에 강인하다는 장점이 있다 (He & Chan 2016).
실내외 장소에 제약없이 지속적인 측위가 가능한 기술은 Inertial Measurement Unit (IMU)를 사용한 Pedestrian Dead Reckoning (PDR) 알고리즘이다. PDR은 걸음 검출, 보폭 추정, 이동 방향 결정의 세 가지 과정을 통해 사용자의 위치를 추정하는 방법이다. 해당 기술은 인프라 지원이 필요하지 않는 독립형 측위 방법으로, 짧은 시간 내에 정확한 측위가 가능하다는 장점이 있다. 그러나 저가형 IMU를 사용하는 경우 직접 적분으로 인한 누적 오차로 인해 위치정보의 정확도는 시간이 지남에 따라 급격히 감소한다. IMU 센서가 발에 장착되는 경우에는 누적 오차를 제거하기 위해 영속도 보정 알고리즘을 사용할 수 있다 (Cho et al. 2020). 그러나 손에 위치하고 있는 스마트폰의 경우에는 영속도를 검출할 수 없기 때문에 GPS, Wi-Fi와 같은 추가적인 보조 자원을 사용하여 오차를 보정해야 한다.
본 논문에서는 실내외 연속복합 측위를 위해 PDR, GPS, Wi-Fi 기술을 통합한 보행자 항법 시스템을 개발하는 것을 목적으로 한다. 이 때 융합을 위한 필터링 방법으로 Extended Kalman Filter (EKF)를 사용한다. GPS와 Wi-Fi 측정치의 정확성이 높으면 PDR의 오차를 효과적으로 보정할 수 있다. 그러나 각 측정치는 신호의 품질이나 외부 간섭으로 인해 이상치가 포함될 수 있다. 특히 Wi-Fi의 경우 실내 공간의 환경 변화와 RSSI의 높은 변동성으로 인해 측위 성능에 직접적인 영향을 미칠 수 있다. 또한 GPS 측정치는 실외에서 실내로 이동할 때 출입문 인근에서 다중 경로 페이딩의 영향이 포함될 수 있다. 이러한 요인들은 측정치의 품질을 저하시켜 필터의 성능을 저감시키는 원인이 된다. 본 논문에서는 해당 문제를 해결하기 위해 Rényi Divergence (RD)를 활용하여 측정치의 이상치를 검출하는 기법을 제안한다. 제안된 기법은 EKF를 기반으로 하는 RD 접근법을 사용한다. 측정치 업데이트 단계에서 잔차 (Residual)와 두 개의 공분산 행렬을 이용하여 RD를 계산한다. 이 후 실험을 통해 임계값을 설정하고, RD 값이 임계값을 초과할 경우 해당 측정치는 이상치로 검출한다. 이상치로 판단된 측정치는 측정치 업데이트 과정에서 제외하고, 순수 PDR만으로 보행자의 위치를 추정하도록 한다. 제안된 기법의 성능은 실 데이터를 기반으로 한 실험을 통해 검증한다.
본 논문은 다음과 같이 구성된다. 2장에서는 스마트폰을 사용한 PDR과 Wi-Fi 전자지문 기법에 대해 설명하고, 3장에서는 PDR/GPS/Wi-Fi 복합항법시스템에서 RD를 이용한 측정치 이상치 검출 방법을 설명한다. 4장에서는 실 환경에서 보행 실험을 통해 이상치 검출 성능을 평가한다. 그리고 마지막 5장에서 결론을 맺는다.
이번 장에서는 스마트폰의 IMU 센서를 사용한 PDR과 Wi-Fi 인프라 기반의 전자지문 측위 기술에 대해 설명한다.
스마트폰은 보행자의 손에 고정된 상태로 위치하며, 화면을 모니터링 하면서 이동하는 형태인 Hand-held 유형으로 PDR을 수행한다. 스마트폰을 사용한 PDR 기법은 Fig. 1과 같이 걸음 검출, 보폭 길이 추정, 헤딩 추정의 3가지 과정으로 구성된다. 먼저 걸음 검출을 위해 Eq. (1)과 같이 가속도 값들을 합산한 하나의 대표값을 생성한다.
$$Acc_{M, t} = \sqrt{Acc_{x, t}^2 + Acc_{y, t}^2 + Acc_{z, t}^2} – g$$
여기서 $Acc_{M, t}$는 생성된 가속도의 크기, $Acc_{i, t}$는 시간 $t$에서 획득한 $i$축 방향의 가속도계 출력 신호, $g$는 중력 성분으로 9.81 m/s2과 같다.
원시 가속도 신호는 신체의 지속적인 떨림으로 인해 간섭과 노이즈가 포함될 수 있다. 따라서 가속도 크기에 대한 신호의 굴곡을 평활화 (smoothing)하기 위해 차단 주파수가 2 Hz인 3차 버터워스 저역통과 필터를 적용하였다. 필터링된 신호는 부드러운 정현파 형태로 변환되어 걸음 검출을 위한 최대 피크를 감지하는 데 더 명확한 굴곡을 생성하게 된다.
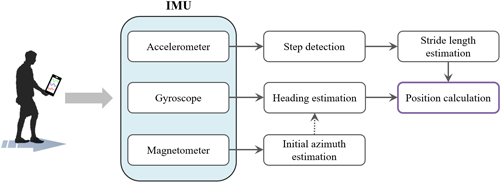
Fig. 1. Structure of PDR using smartphone.
보폭 길이는 검출된 두 걸음 지점 사이의 거리를 의미한다. 이는 Eq. (2)와 같이 각 걸음 동안에 가속도계 출력에 의해 결정될 수 있는 분산과 걸음 주파수 간의 선형 조합을 통해 추정한다 (Kwon et al. 2023).
$$\text{Stride Length} = \alpha \cdot F + \beta \cdot V + \gamma$$
$$\text{Walking Distance} = \sum_{k=1}^{n} (\alpha \cdot F_k + \beta \cdot V_k + \gamma)$$
여기서 $F_k$와 $V_k$는 각각 $k$번째 걸음에서의 걸음 주파수와 가속도 크기의 분산을 나타내며, $\alpha$, $\beta$는 걸음 매개변수에 대한 가중치, $\gamma$는 일정 상수를 의미한다. 보행 특성에 따라 $\alpha$, $\beta$, $\gamma$는 서로 상이한 값을 가지며, 사전 실험을 기반으로 한 최소자승법을 통해 보정된 매개변수를 계산할 수 있다.
보행자의 이동 방향은 3축 자이로와 지자계를 이용하여 계산할 수 있다. 지자계는 절대 방위각을 계산할 수 있지만 주변 환경의 금속 물체나 전자기파와 같은 자기장 간섭에 민감하게 반응한다 (Almeida et al. 2021). 따라서 본 연구에서는 보행자가 처음 정지할 때 초기 방위각을 설정하기 위한 절대 방향 정보로만 사용한다. 이를 위해 스마트폰 내부에 존재하는 자기장의 왜곡을 제거하기 위해 교정 (calibration) 과정을 거친다. 이 후 정지 시간 동안 출력된 지자계 데이터의 평균 값을 사용하여 초기 방위각을 계산한다 (Cho 2014).
보행자가 이동 중에 변화되는 방향 정보는 자이로 센서를 이용하여 계산한다. 스마트폰의 방향이 보행자의 이동 방향과 동일하며, 스마트폰이 수평을 이룬다고 가정한다면 수직 방향의 자이로 데이터를 직접 적분하여 방향 정보를 계산할 수 있다. 이와 반면에 자이로 출력값을 이용하여 스마트폰의 자세정보를 갱신하는 경우에는 쿼터니언을 사용하여 계산할 수 있다 (Titterton & Weston 2004). 자이로의 출력 주기로 갱신된 쿼터니언은 오일러각으로 변환하여 자세 정보를 획득할 수 있다. 앞선 과정에서 보폭 길이와 방향 정보가 추정되면 Eq. (4)를 통해 위치를 계산할 수 있다.
$$\begin{bmatrix}
Lat_k \\
Lon_k
\end{bmatrix}
=
\begin{bmatrix}
Lat_{k-1} \\
Lon_{k-1}
\end{bmatrix}
+
\begin{bmatrix}
\frac{SL_k \cdot \cos\psi_k}{R_{m, k-1}} \\
\frac{SL_k \cdot \sin\psi_k}{R_{t, k-1} \cdot \cos Lat_{k-1}}
\end{bmatrix}$$
여기서 $\begin{bmatrix} Lat_k & Lon_k \end{bmatrix}^T$와 $\begin{bmatrix} Lat_{k-1} & Lon_{k-1} \end{bmatrix}^T$는 각각 $k$와 $k-1$번째 걸음에서의 위도와 경도를 나타내고, $SL_k$와 $\psi _k$는 각각 $k$번째 걸음에서의 보폭 길이와 헤딩 정보를 의미한다. 그리고 $R_m$과 $R_t$는 각각 위도와 경도방향의 지구 타원체 반경을 나타낸다 (Titterton & Weston 2004).
Wi-Fi 전자지문 기술은 Wi-Fi 신호 특성과 물리적 위치 간의 RSSI 패턴에 대한 상관 관계를 활용하는 방법이다. Wi-Fi 전자지문은 오프라인 단계와 온라인 단계로 구성된다. 먼저 오프라인 단계에서는 특정 공간의 각 기준점에서 Wi-Fi RSSI를 수집하고, 해당 기준점의 좌표와 결합하여 데이터베이스를 구축한다. 기준점별로 수신 범위 내에 존재하는 여러 AP들로 인해 고유한 신호 패턴이 데이터베이스에 저장된다.
온라인 단계에서는 Fig. 2와 같이 사용자의 스마트폰이 실시간으로 측정한 RSSI 패턴을 데이터베이스에 저장된 RSSI 세트와 매칭 알고리즘을 통해 사용자의 위치를 추정한다. 매칭 계산을 위해 다양한 측위 알고리즘이 존재하지만 비교적 구현이 간단하고 보편적으로 적용되는 알고리즘은 k-Nearest Neighbor (kNN)이다 (Hou et al. 2023). kNN은 RSSI의 유사도 거리에 기반한 방법으로, Eq. (5)와 같이 Euclidean 거리를 사용할 수 있다.
$$d_i = \sqrt{\sum_{j=1}^{n_i} \left( RSSI_{meas, l}^j – RSSI_{DB, i}^j \right)^2}$$
여기서 $d_i$는 $i$번째 기준점에서 계산된 RSSI 패턴의 유사도, $RSSI_{meas, l}^j$는 위치 $l$에서 측정된 $j$번째 $RSSI$, $RSSI_{DB, i}^j$는 데이터베이스에 저장된 $i$번째 기준점에 대한 $j$번째 $RSSI$를 의미한다. 그리고 $n_i$는 $i$번째 기준점에서 획득된 Wi-Fi AP의 전체 개수를 나타낸다.
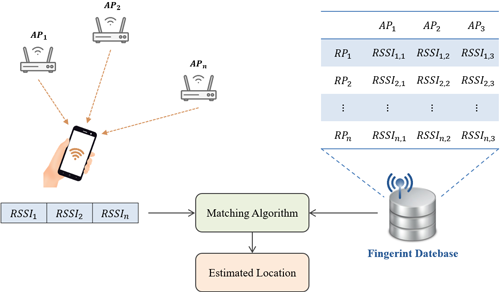
Fig. 2. The principle of WiFi fingerprinting.
Eq. (5)를 통해 계산된 거리 값을 기반으로 비교적 신뢰할 수 있는 최종 위치를 계산하기 위해 Weighted k-Nearest Neighbor (WkNN) 기법을 사용한다. WkNN은 kNN 개념을 확장하여 각 기준점에 가중치를 부여함으로써 더 정밀한 위치 추정을 가능하게 한다. WkNN은 기준점의 유사도 순위에 따라 가중치를 비례적으로 적용하는 방식으로 Eq. (6)과 같이 계산할 수 있다.
$$(Lat’, Lon’) = \frac{\sum_{i=1}^{k} w_i \cdot (Lat_i, Lon_i)}{\sum_{i=1}^{k} w_i}$$
여기서 $(Lat’, Lon’)$와 $(Lat_i, Lon_i)$는 각각 추정된 위치정보와 $i$번째 후보 기준점에 대한 좌표를 나타내고, $w_i$는 $i$번째 후보 기준점에 대한 가중치를 의미한다. 가중치는 Eq. (7)과 같이 거리의 역수로 할당하여 유사도가 높은 기준점일수록 높은 가중치가 부여된다.
$$w_i = \frac{1}{d_i + \epsilon}$$
여기서 $d_i$는 $i$번째 기준점에서 계산된 RSSI 패턴의 유사도 거리를 나타내고, $\epsilon$은 동일한 신호 패턴일 때 가중치가 무한대로 발산하는 것을 방지하기 위한 작은 상수 값을 나타낸다.
이번 장에서는 PDR/GPS/Wi-Fi 복합측위 시스템에서 Rényi Divergence 기반으로 이상치를 검출하는 기법에 대해 자세히 설명한다. Fig. 3은 제안된 시스템의 전체적인 구조를 나타낸 것이다. PDR 은 자율적이며 외부 간섭에 취약하지 않기 때문에 실내외 환경 모두에서 활용될 수 있지만, 센서 오차로 인해 시간이 경과함에 따라 오차가 점차 증가하게 된다. 이러한 오차를 보정하기 위해서는 독립적인 위치 정보를 제공하는 다른 기술과의 융합이 필수적이다. 이를 위해 실외 환경에서는 GPS, 실내 공간에서는 Wi-Fi 전자지문 측위 정보를 사용하도록 한다. 측정치 선택을 위한 실내외 환경 구분 정보는 GPS 측정 정보인 Horizontal Dilution of Precision (HDOP)를 활용하며, GPS 측정치가 제공되지 않거나 HDOP 값이 임계값 ($\tau$)을 초과할 경우 해당 환경을 실내로 판단한다. 측정치 선택이 완료되면 EKF 과정을 통해 PDR 오차를 보상하기 위한 보정 정보를 계산할 수 있다. 그러나 필터링 과정에서 사용되는 측정치가 연속적이지 않거나 큰 오차를 포함하는 경우에는 필터의 성능이 급격히 저하되는 문제가 발생하게 된다. 이러한 문제를 해결하기 위해 본 논문에서는 Fig. 3의 빨간색 점선으로 표시된 부분과 같이 EKF 과정에서 RD를 함께 계산하여 측정치의 이상치 여부를 판단하도록 한다.
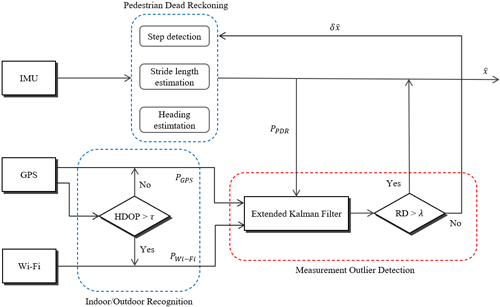
Fig. 3. Structure of PDR/GPS/Wi-Fi-integrated pedestrian navigation system applying RD-based measurement outlier detection technique.
RD는 두 확률분포 간이 차이를 정량적으로 측정하는 지표로, 정보 이론과 통계학에서 주로 사용된다. RD는 Kullback-Leibler Divergence (KLD) 방법을 일반화한 형태로, 두 확률 분포 간의 유사성이나 차이를 평가하는 데 활용된다. RD는 두 확률 분포 $P(x)$와 $Q(x)에 대해 Eq. (8)과 같이 정의된다 (Thierrin et al. 2022).
$$RD_{\alpha} (P \parallel Q) = \frac{1}{\alpha – 1} \log \left( \sum_{x} P(x)^{\alpha} Q(x)^{1-\alpha} \right)$$
여기서 $\alpha$는 비대칭성을 조절하는 매개변수로, $\alpha$의 크기에 따라 RD의 성질이 달라진다. $\alpha$값은 실수 범위에서 정의되며, $\alpha \geq 0$이고 $\alpha \neq 1$일 때 유효하다. 만약 $\alpha > 1$인 경우 $P(x)^{\alpha} Q(x)^{1-\alpha}$는 $P(x)^{\alpha} / Q(x)^{1-\alpha}$로 변환되며, $0/0=0$과 $\frac{x}{0} = \infty \quad (x > 0)$인 규칙이 적용된다. RD는 $\alpha$값에 따라 분포 간의 관계를 다르게 해석할 수 있다는 특징을 갖는다.
$\alpha =1$일 경우, RD는 KLD와 동일한 형태를 가지며 Eq. (9)와 같이 나타낼 수 있다.
$$RD_{1} (P \parallel Q) = \sum_{x} P(x) \log \left( \frac{P(x)}{Q(x)} \right)$$
KLD는 분포 $P(x)$가 다른 분포인 $Q(x)$와 비교하여 얼마나 다른지를 측정하는 방법이다. 즉, 두 분포에 대한 차이를 $P(x)$를 기준으로 측정하는 것이다. 두 확률 분포는 대칭 행렬이 아니기 때문에 $RD_{1}(P \parallel Q) \neq RD_{1}(Q \parallel P)$인 조건을 가지며, 두 확률 분포는 동일한 표본 공간을 가져야 한다 (van Erven & Harremos 2014).
$\alpha =0.5$일 경우, Bhattacharyya 거리와 일치하며, 이는 두 확률 분포 간의 유사성을 평가하는 데 유용한 값으로 사용된다. $\alpha =0$일 경우, RD는 두 분포가 동일할 때 log 확률로 수렴하며 Eq. (10)과 같이 극한으로 표현할 수 있다.
$$\lim_{\alpha \to 0} RD_{\alpha} (P \parallel Q) = – \log \left( \sum_{x} Q(x) [P(x) > 0] \right)$$
여기서 $[P(x) > 0]$는 조건을 만족하면 ‘1’, 그렇지 않으면 ‘0’으로 반환된다. 즉, 분포 $P(x)$가 ‘0’이 아닌 경우 분포 $Q(x)$를 합산한 후 로그 값을 취하게 된다. 만약 두 분포의 유사도가 높다면 RD는 0으로 수렴하게 된다.
위와 같은 특성으로 인해 RD는 특정 응용 분야에서 분포 간의 유사성을 평가하는 데 유용한 지표로 사용된다. 데이터 마이닝 에서는 데이터의 군집화나 분류 과정에서 두 데이터 집합 간의 차이를 분석하는 데 활용될 수 있으며, 통계적 분석에서는 이상치 탐지 및 데이터의 패턴 분석에 사용할 수 있다 (Makkawi et al. 2021).
스마트폰 기반 보행자의 실내외 연속측위를 위해 IMU 센서를 사용한 PDR과 두 개의 인프라 보조 자원이 결합된 보행자 항법 시스템을 설계한다. PDR의 비선형성을 고려하여 EKF 기반으로 항법필터를 설계하며, Eq. (11)과 같이 시간 $k$에서의 오차 상태변수를 설정한다.
$$\delta x_k = \begin{bmatrix} \delta L_k & \delta l_k & \delta SL_k & \delta \psi_k & \varepsilon_k \end{bmatrix}$$
여기서 $\delta L_k$와 $\delta Sl_k$는 각각 위도와 경도오차, $\delta SL_k$는 보폭 길이 오차, $\delta \psi_k$는 방향 오차, $\varepsilon_k$는 자이로 바이어스를 나타낸다. 상태 천이 모델은 Eq. (12)와 같이 표현할 수 있다.
$$\delta x_{k+1} = \Phi_k \delta x_k + w_k, \quad w_k \sim N(0, Q_k)$$
여기서 $w_k$는 공정 잡음으로 공분산 행렬은 $Q_k = E(w_k w_k^T)$으로 정의된다. $\Phi_k$는 상태 천이 행렬로 PDR의 오차 모델을 기반으로 Eq. (13)과 같이 구성할 수 있다.
$$\begin{bmatrix}
1 & 0 & \cos \psi_k / R_{m, k} & -SL_k \sin \psi_k / R_{m, k} & 0 \\
0 & 1 & \sin \psi_k / (R_{t, k} \cos L_k) & SL_k \cos \psi_k / (R_{t, k} \cos L_k) & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & Ts \\
0 & 0 & 0 & 0 & 1 \\
\end{bmatrix}$$
여기서 $T_s$는 한 걸음 동안의 시간을 의미한다.
측정치 모델은 Eq. (14)와 같이 표현할 수 있다.
$$y_k = H \delta x_k + v_k, \quad v_k \sim N(0, R_k)$$
여기서 $v_k$는 측정치 잡음으로 공분산 행렬은 $R_k = E(v_k v_k^T)$로 정의된다. $H$는 측정치 행렬로 위치 정보만 측정치로 사용하는 경우 Eq. (15)와 같이 나타낼 수 있다.
$$H = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{bmatrix}$$
EKF 과정에서 오차 공분산 행렬에 대한 시간 전파 (time propagation)와 측정치 갱신 (measurement update) 과정은 각각 Eqs. (16, 17)과 같이 수행된다.
$$P_{k+1}^{-} = \Phi_k P_k \Phi_k^T + Q_k$$
$$\begin{align}
\delta \hat{x}_k &= K_k z_k \tag{17a} \\
P_k &= (I_{5 \times 5} – K_k H) P_k^- \tag{17b}
\end{align}$$
여기서 $K_k = P_k^- H^T (H P_k^- H^T + R_k)^{-1}$으로 칼만 이득을 나타내고, $z_k$는 잔차로 PDR 위치와 측정치 위치의 차이를 의미한다.
두 개의 확률 밀도 함수 $P(x)$와 $Q(x)$가 주어진 경우, RD는 Eq. (18)과 같이 정의된다. 그러나 두 개의 $n$차원 가우시안 분포 $P(x) = N(\mu_0, \Sigma_0)$와 $Q(x) = N(\mu_1, \Sigma_1)$에 대해서는 Eq. (18)과 같이 다변량 (Multivariate) 가우시안의 형태로 표현할 수 있다 (Gil et al. 2013, Chen & Kia 2021).
$$RD(P \parallel Q) = \frac{\alpha}{2} (\mu_0 – \mu_1)^T (\Sigma_\alpha^*)^{-1} (\mu_0 – \mu_1) – \frac{1}{2(\alpha – 1)} \ln \frac{|\Sigma_0^*|^{1-\alpha} |\Sigma_1^*|^\alpha}{|\Sigma_\alpha^*|} \tag{18}$$
여기서 $\Sigma^* = \alpha \Sigma_1 + (1 – \alpha) \Sigma_0 > 0$이며, 해당 조건을 만족시키기 위해 $\alpha$를 0과 1 사이의 범위에서 선택되어야 한다. 이 때 두 분포가 동일할 경우 RD는 0이 된다.
오차가 큰 측정치에 대해서는 Eq. (17a)에서 $z_k$값을 왜곡시켜 오차 상태 추정치를 손상시킬 수 있다. 이와 반대로 측정치가 연속적이고 오차가 없는 경우에는 갱신된 정보 $(\delta \hat{x}_k, P_k)$와 시간 전파된 정보 $(\delta \hat{x}_k^-, P_k^-)$는 유사한 형태로 표현될 것이다. 여기서 시간 전파된 $\delta \hat{x}_k^-$는 EKF에서 피드백으로 오차 보상을 해주기 때문에 $0_{5 \times 1}$로 표현된다. 따라서 Eq. (18)은 EKF 과정에서 계산된 Eqs. (16, 17)을 이용하여 Eq. (19)와 같이 나타낼 수 있다.
$$\begin{align} RD &= \frac{\alpha}{2} (\delta \hat{x}_k^T (P_k^*)^{-1} \delta \hat{x}_k) – \frac{1}{2(\alpha – 1)} \ln \frac{\det(P_k^*)}{\det(P_k^-)^{1-\alpha} \det(P_k)^\alpha} \notag \\ &= \frac{\alpha}{2} z_k^T K_k^T (P_k^*)^{-1} K_k z_k – \frac{1}{2(\alpha – 1)} \ln \frac{\det(P_k^*)}{\det(P_k^-)^{1-\alpha} \det(P_k)^\alpha} \tag{19} \end{align}$$
여기서 $P_k^* = \alpha P_k + (1 – \alpha) P_k^-$이다. 오차가 큰 측정치를 사용할 때 RD 척도는 큰 편차로 계산될 것이다.
RD를 사용하여 이상치를 검출하기 위해서는 기준이 되는 임계값이 필요하다. 따라서 임계값은 정상 측정치의 RD 값이 카이제곱 분포를 따른다고 가정하고, 해당 분포의 95%의 지점을 임계값 $\lambda$로 설정한다. 이 과정은 많은 실험 데이터를 통해 정상적으로 획득된 측정치의 분포 특성을 분석하여 통계적인 방법으로 결정된다. 만약 정상적인 측정치는 $H_0$, 오차가 큰 측정치는 $H_1$로 가정하면 Eq. (20)과 같이 표현할 수 있다.
$$RD \overset{H_0}{<} \lambda, \quad RD \overset{H_1}{>} \lambda \tag{20}$$
따라서 RD 값이 0과 $\lambda$사이에 존재하는 경우, $H_0$은 갱신 과정에 필요한 측정치로 사용된다. 그러나 RD 값이 $\lambda$를 초과한다면, $H_1$은 이상치로 검출되어 갱신 과정을 수행하지 않는다. 즉, 해당 시점에서는 순수 PDR으로만 위치를 계산한다.
이 논문에서는 RD를 사용하여 측정치 이상치 검출 기법을 적용한 PDR/GPS/Wi-Fi 복합측위 시스템의 성능을 검증하기 위해 실시험을 진행하였다.
실험을 위한 테스트 환경은 경일대학교 제 1공학관 2층 실내 복도와 인근 실외 환경으로 설정하였다. 실험 장비는 Samsung Galaxy S21 Ultra (Android version 14) 모델의 스마트폰을 이용하였다. 센서 및 측정치 획득은 Android Studio 환경에서 ETRI와 협업으로 개발중인 어플리케이션을 사용하였다. IMU 센서 데이터는 100 Hz로 센싱되며, GPS 측정 정보는 1초, Wi-Fi 신호는 약 2초 주기로 획득된다. 실내외 판단 기준으로는 GPS에서 측정되는 HDOP 정보를 활용한다. 실내 공간에서 GPS 측정 정보는 수신되지 않거나 큰 오차를 갖는 위치 정보를 제공할 수 있다. 이 경우 HDOP 정보는 큰 값을 가지게 된다. 따라서 HDOP 정보가 $\tau$로 설정된 임계값을 초과하는 경우에는 실내 공간으로 판단하여 Wi-Fi 무선 측위 정보를 측정치로 사용한다. 다양한 환경과 여러 실험을 통해 $\tau$는 7 m로 설정하였다. RD 계산을 위한 $\alpha$값은 0과 0.5 사이로 설정한 경우 시간 전파된 공분산에 대해 높은 가중치, 0.5와 1 사이로 적용할 경우 갱신된 공분산에 큰 가중치가 부여된다. 본 연구에서는 시간 전파 과정에서 보행자의 위치는 일정 범위 내에 존재하고, 측정치의 이상치로 인해 편차가 증가할 것이라고 판단하여 $\alpha$값을 0.1로 설정하였다. Fig. 4는 실험을 위해 설정된 실제 이동 경로와 데이터베이스 구축을 위한 기준점의 위치를 나타낸 것이다. 여기서 기준 위치의 간격은 약 2.25 m로 구성하였다. 실험을 위한 시나리오는 실외에서 실내 공간으로 들어서는 A에서 B 지점으로 보행하는 경우와 실내에서 실외 환경으로 변화되는 B에서 A 지점으로 보행하는 경우로 설정하였다.
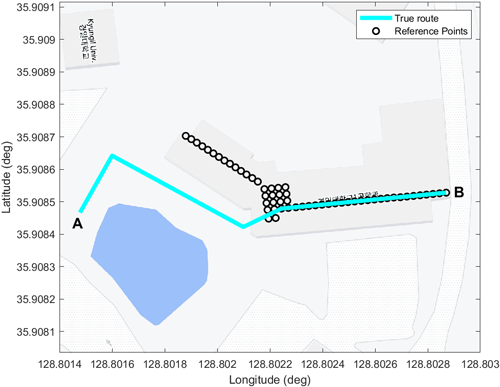
Fig. 4. The true movement route and locations of reference points.
융합 필터 과정에서 계산된 RD를 사용하여 측정치의 이상치를 검출하기 전과 후의 측위 성능을 비교분석 하였다. 먼저 Fig. 5a는 실외에서 실내로 보행 (A에서 B 지점으로 이동)하는 동안 획득된 GPS의 위치정보를 나타낸 것이며, 검정색 점선을 확대한 구간은 오른쪽 그림과 같다. 실내 공간으로 환경이 변화된 후 지속적인 보행을 하는 동안에는 GPS 측정치는 제공되지 않지만 빨간색 점선으로 표시한 부분과 같이 출입문 근처에서 일정 시간 동안 위치가 머무르는 것을 확인할 수 있다. 이 때, 출입문 인근에 존재하는 GPS 위치의 개수는 11개이다. Fig. 5b는 GPS의 HDOP를 나타낸 것이다.
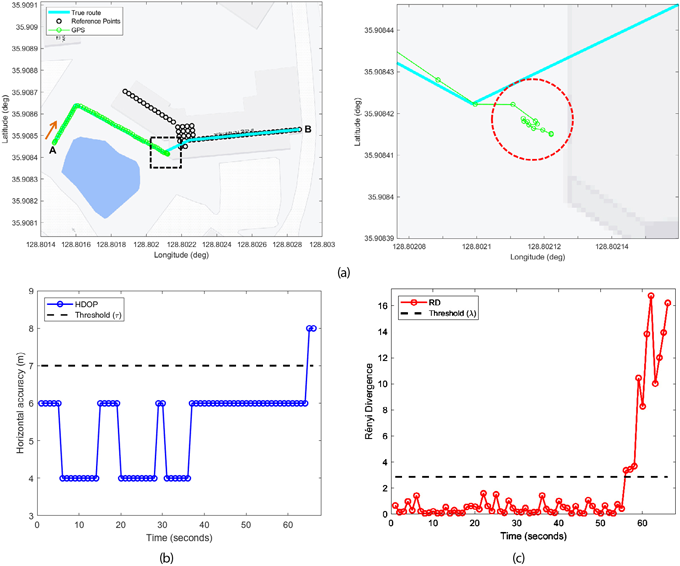
Fig. 5. GPS measurements acquired while walking from outdoors to indoors (Moving from A to B). (a) location, (b) HDOP, (c) RD.
HDOP를 이용하여 실내 공간으로 변화됨을 판단하고, 융합을 위한 측정치를 Wi-Fi 측위 결과로 변환시킬 수 있다. 그러나 출입문 인근에서 머무르는 GPS 위치에 대한 HDOP 값은 측정치를 변환시키기 위한 임계값에 바로 도달되지 않으며, 이는 결국 측정치의 이상치 정보가 된다. 측정치의 이상치 검출을 위해 계산된 RD의 정보는 Fig. 5c와 같다. 보행자는 출입문 통과 후 실내 공간에서 도착 지점을 향해 걸어가고 있지만 GPS의 이상치로 인해 측위 결과가 출입문 인근으로 이동되는 영향을 보인다. 이는 Fig. 6a의 연속 측위 결과에서 출입문 인근을 확대한 오른쪽 그림에서 확인할 수 있다. 이러한 측정치의 이상치는 필터 과정에 계산된 RD의 편차를 증가시키게 하는 원인이 되며, 11개의 측정치에 대한 이상치가 모두 검출됨을 Fig. 5c에서 확인할 수 있다. Fig. 6b는 측정치가 이상치로 판단된 시점에서 순수 PDR으로만 측위를 진행한 결과를 나타낸 것이다. 그림에서 보는 바와 같이 RD를 이용하여 이상치를 검출함으로써 실내외 환경이 변화되는 구간에서 정확한 항법 정보로 추정될 수 있음을 확인할 수 있다. 이 때, 측정치가 Wi-Fi로 변환되는 시점에서는 RD 계산을 중지하고, 일정 시간이 지난 후에 이상치를 다시 탐색하도록 한다.
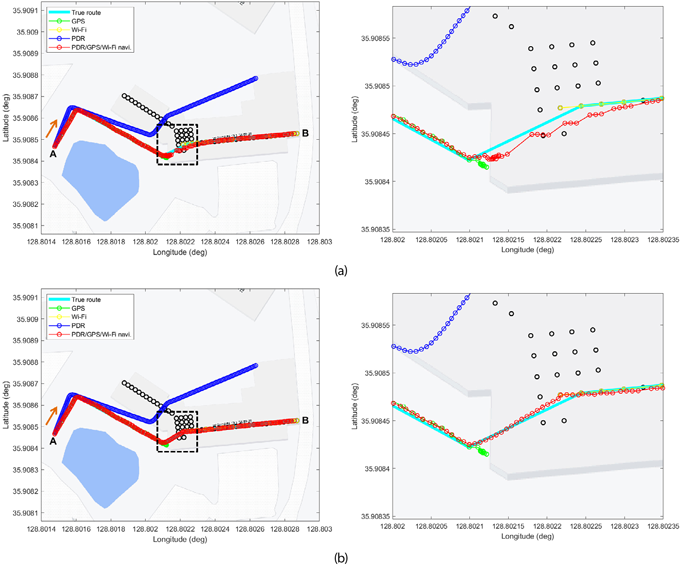
Fig. 6. Continuous positioning results when walking from outdoors to indoors. (a) before outlier removal, (b) after outlier removal.
Fig. 7은 실내에서 실외로 보행(B에서 A 지점으로 이동)하는 동안에 획득 및 추정된 측정치의 위치정보를 나타낸 것이다. 먼저 Fig. 7a의 왼쪽 그림은 GPS의 위치를 나타낸 것으로, 빨간색 원으로 표시된 부분에서 큰 오차를 갖는 위치정보가 획득됨을 확인할 수 있다. 이 위치에 대한 HDOP 값은 200 m 이상의 높은 편차로 측정되어, Fig. 7a의 오른쪽 그림에서의 HDOP는 해당 측정치를 제외하고 나타내었다. Fig. 7b는 Wi-Fi 전자지문 측위 결과를 나타낸 것으로 검정색 점선으로 표시한 영역을 오른쪽 그림과 같이 확대하여 나타내었다. 해당 그림을 보면 기준점의 간격이 격자 공간으로 세분화되어 있는 것을 확인할 수 있다. 이 영역에서 위치한 기준점은 양쪽 직선 경로에 대한 모든 AP 신호가 스캔 될 수 있는 범위에 존재하고 있기 때문에 인근 기준점 마다 유사한 신호 패턴이 저장될 수 있다. 또한 AP 신호의 특성상 RSSI의 높은 변동성과 구조물과 같은 환경 변화에 민감하다. 이러한 영향으로 인해 실제 이동 경로와 비교하여 Wi-Fi 측위 결과의 오차 양상이 큰 것을 확인할 수 있다. 또한 실외 환경으로 변화되는 구간에서는 정상적인 GPS 위치가 제공되기까지 일정 시간이 소요된다.
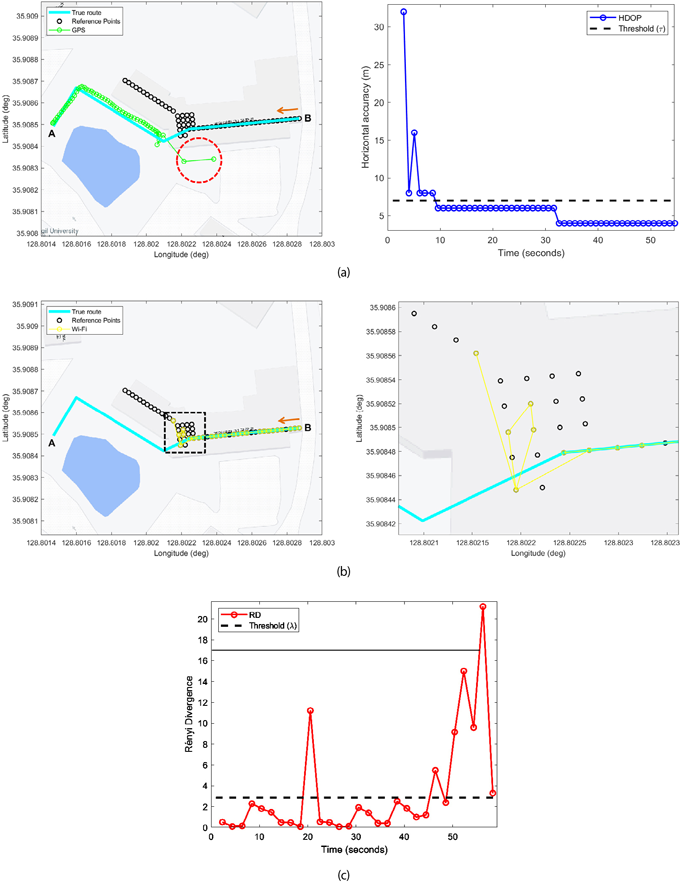
Fig. 7. Measurements acquired while walking from indoors to outdoors (Moving from B to A). (a) GPS location and HDOP, (b) Wi-Fi Fingerprinting, (c) RD of WiFi Fingerprinting.
즉, Fig. 7a 오른쪽 그림에서 나타낸 HDOP 정보에서 실외 환경으로 변화된 후 GPS 측정치가 안정되기까지 약 6초정도 소요됨을 확인할 수 있다. 이는 실외에서 Wi-Fi 측위 결과가 측정치로 사용되는 문제를 초래한다. 이러한 문제들을 종합하여 보면 Fig. 8a의 연속 측위 결과에서 볼 수 있듯이 큰 오차를 갖는 측정치의 영향으로 인해 추정된 위치정보의 정확성을 보장할 수 없게 된다. 따라서 필터 성능 저감 문제를 해결하기 위해 Fig. 7c의 RD 정보를 사용하여 측정치의 이상치를 검출하도록 하였다. 검출된 정보를 기반으로 Wi-Fi 전자지문 결과에 대한 이상치를 필터 과정에 제외함으로써 Fig. 8b에서 나타낸 것과 같이 항법 정보의 정확성이 향상됨을 확인할 수 있었다. Table 1은 실내외 환경이 변화되는 시나리오마다 3번씩 실험을 진행하여 RD 기반 이상치 검출 성능을 평가한 지표로 총 개수 대비 약 90% 이상으로 이상치가 검출됨을 확인할 수 있었다. 해당 지표에서 이상치가 미검출된 이유는 RD 값이 설정된 임계값에 도달하지 않았기 때문이다. 많은 실험을 기반으로 임계값을 설정하였지만 고정된 값은 모든 데이터의 특성을 반영하기 어렵다. 따라서 실시간 데이터 분석 또는 머신러닝 기법을 활용하여 현재 데이터에 적합한 임계값을 동적으로 설정하는 것이 필요하다.
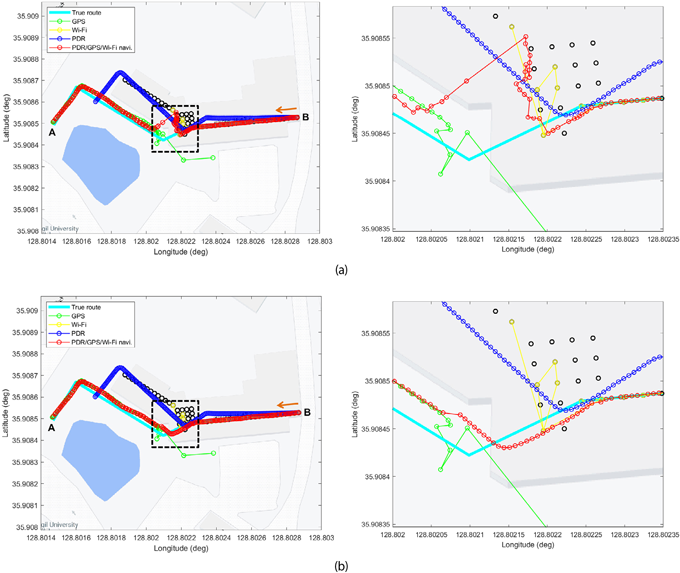
Fig. 8. Continuous positioning results when walking from indoors to outdoors. (a) before outlier removal, (b) after outlier removal.
Table 1. Outlier detection performance using RD.
| Num. | The number of detected outliers according to walking scenarios | |||
|---|---|---|---|---|
| From outdoors to indoors | From indoors to outdoors | |||
| True number | Detected number | True number | Detected number | |
| 1 | 15 | 13 | 17 | 16 |
| 2 | 9 | 9 | 17 | 16 |
| 3 | 12 | 10 | 13 | 11 |
| Sum | 36 | 32 | 47 | 43 |
이 논문은 스마트폰을 이용한 보행자의 실내외 연속측위를 위해 PDR/GPS/Wi-Fi 복합측위 시스템을 개발하는 것을 목적으로 한다. 각 기술의 장단점을 상호 보완적으로 활용하여 단일 센서에 의존할 때 발생할 수 있는 측위 오차를 보정할 수 있다. 실내외 제약을 받지 않는 PDR 기법의 비선형성을 고려하여 EKF를 구현하고, GPS와 Wi-Fi 신호로 추정된 위치정보를 필터의 측정치로 사용하였다. 또한, GPS의 HDOP 정보를 측정치 선택을 위한 실내외 판단 기준으로 활용하였다. 그러나 특정 공간에서 비정상적인 측정치가 제공되는 취약 구간이 존재하며, 이는 필터의 성능을 저하시키고 추정된 위치정보의 오차를 증가시키는 원인이 된다. 이번 연구에서는 이러한 문제를 해결하기 위해 필터 과정에서 RD를 함께 계산하도록 하였다. 이를 위해 RD를 다변량 가우시안 분포의 형태로 변환하여, 추정치와 측정치의 차이뿐만 아니라 두 공분산도 함께 고려하였다. 추정치는 일정 범위 내에 위치하지만 측정치의 오차로 인해 RD의 편차는 증가하게 된다. 이러한 원리를 기반으로 RD 값이 큰 시점에 대해서는 해당 측정치를 이상치로 판단하여, 순수 PDR으로만 측위가 진행되도록 설계하였다. 실 데이터를 기반으로 테스트를 진행한 결과 실내외 환경 전환 시 발생한 측정치의 이상치를 약 90%의 확률로 검출할 수 있음을 확인하였다. 이 연구에서 제안된 기술을 통해 보행자 항법 시스템의 신뢰성과 견고성이 개선되어 다양한 응용 분야에 활용될 수 있을 것으로 기대된다.
This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant RS-2022-00141819).
Jae Uk Kwon contributed to the design and implementation of the algorithms and to the writing of the manuscript. Seong Yun Cho led the research and reviewed the manuscript as the person in charge of the service project. JaeJun Yoo and SeongHun Seo supervised the research as original project managers and provided related information.
The authors declare no conflict of interest.
Almeida, D., Pedrosa, E., & Curado, F. 2021, Magnetic Mapping for Robot Navigation in Indoor Environments, 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 Nov – 02 Dec 2021, pp.103-108. https://doi.org/10.1109/IPIN51156.2021.9662528
Chen, C. & Kia, S. S. 2021, A Rényi Divergence Based Approach to Fault Detection and Exclusion for Tightly Coupled GNSS/INS System, Proceedings of the 2021 International Technical Meeting of The Institute of Navigation, St. Louis, Missouri, 25-28 January 2021, pp.674-687. https://doi.org/10.33012/2021.17859
Cho, S. Y. 2014, Biaxial Accelerometer-based Magnetic Compass Module Calibration and Analysis of Azimuth Computational Errors Caused by Accelerometer Errors, Journal of Institute of Control, Robotics and Systems, 20, 149-156. https://doi.org/10.5302/J.ICROS.2014.13.9008
Cho, S. Y., Lee, J. H., & Park, C. G. 2020, Stable Zero-Velocity Detection Method Regardless of Walking Speed for Foot-Mounted PDR, Journal of Positioning, Navigation, and Timing, 9, 33-42. https://doi.org/10.11003/JPNT.2020.9.1.33
Gil, M., Alajaji, F., & Linder, T. 2013, Rényi divergence measures for commonly used univariate continuous distributions, Information Sciences, 249, 124-131. https://doi.org/10.1016/j.ins.2013.06.018
Hou, C., Xie, Y., & Zhang, Z. 2023, FCLoc: A Novel Indoor Wi-Fi Fingerprints Localization Approach to Enhance Robustness and Positioning Accuracy, IEEE Sensors Journal, 23, 7153-7167. https://doi.org/10.1109/JSEN.2022.3229476
He, S. & Chan. S.-H. G. 2016, Wi-Fi Fingerprint-Based Indoor Positioning: Recent Advances and Comparisons, IEEE Communications Surveys & Tutorials, 18, 466-490. https://doi.org/10.1109/COMST.2015.2464084
Kwon, J. U., Chae, M. S., Cho, E. Y., & Cho, S. Y. 2023, Fast Generation of Wi-Fi Positioning Fingerprint Database Using Reference Location Information Acquired Based on 1D-PDR, Proceedings of the Work-in-Progress Papers at the 13th International Conference on Indoor Positioning and Indoor Navigation (IPIN-WiP 2023), Nuremberg, Germany, 25-28 September 2023.
Kwon, J. U. & Cho, S. Y. 2021, DNN-based LTE Signal Propagation Modelling for Positioning Fingerprint DB Generation, Journal of Positioning, Navigation, and Timing, 10, 55-66. https://doi.org/10.11003/JPNT.2021.10.1.55
Leitch, S. G., Ahmed, Q. Z., Abbas, W. B., Hafeez, M., Laziridis, P. I., et al. 2023, On Indoor Localization Using WiFi, BLE, UWB, and IMU Technologies, Sensors, 23, 1-25. https://doi.org/10.3390/s23208598
Ma, Z. & Shi, K. 2023, Few-Shot Learning for WiFi Fingerprinting Indoor Positioning, MDPI Sensors, 23, 1-18. https://doi.org/10.3390/s23208458
Makkawi, K., Ait-Tmazirte, N., Najjar, M. E. B. E., & Moubayed, N. 2021, Adaptive Diagnosis for Fault Tolerant Data Fusion Based on α-Rényi Divergence Strategy for Vehicle Localization, Entropy, 23, 1-27. https://doi.org/10.3390/e23040463
Thierrin, F. C., Alajaji, F., & Linder, T. 2022, Rényi Cross-Entropy Measures for Common Distributions and Processes with Memory, Entropy, 24, 1-9. https://doi.org/10.3390/e24101417
Titterton, D. & Weston, J. 2004, Strapdown Inertial Navigation Technology, 2nd ed. (London: Peregrinus).
van Erven, T. & Harremos, P. 2014, Rényi Divergence and Kullback-Leibler Divergence, IEEE Transactions on Information Theory, 60, 3797-3820. https://doi.org/10.1109/TIT.2014.2320500