1Institute of AI Convergence, Chosun University, Gwangju 61452, Korea
2Interdisciplinary Program in IT-Bio Convergence System, School of Electronic Engineering, Chosun University, Gwangju 61452, Korea
†Corresponding Author: Suk-seung Hwang, E-mail: hwangss@chosun.ac.kr
Citation: Kim, T.-y., & Hwang, S.-s., 2024, Computational Complexity Analysis of Cascade AOA Estimation Algorithm Based on Massive Array Antenna Configuration, Journal of Positioning, Navigation, and Timing, 13, 277-287.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 September, Volume 13, Issue 3, pages 277-287. https://doi.org/10.11003/JPNT.2024.13.3.277
Received on Aug 08, 2024, Revised on Aug 27, 2024, Accepted on Sep 04, 2024, Published on Sep 15, 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In satellite systems, efficient communication and observation require identifying of specific signal arrival points using onboard antenna systems. When utilizing massive array antennas to estimate the angle of arrival (AOA) of signals, traditional high-performance AOA estimation algorithms such as Multiple Signal Classification (MUSIC) encounter extremely high complexity due to the numerous individual antenna elements. Although, in order to improve this computational complexity problem, the cascade AOA estimation algorithm with CAPON and beamspace-MUSIC was recently proposed, the comparison of the computational complexity of the proposed algorithm across different massive array antenna configurations has not yet been conducted. In this paper, we provide the analyzed results of the computational complexity of the proposed cascade algorithm based on various massive array antennas, and determine an optimal antenna configuration for the efficient AOA estimation in satellite systems.
massive array antenna, cascade algorithm, computational complexity analysis, AOA estimation
위성은 지형적 영향을 받지 않으며 여러 궤도의 위성 혹은 위성군을 활용하여 연속적인 임무 수행이 가능하기에 통신, 지구 관측, 국방 등 다양한 분야에서 활용되고 있다. 위성용 안테나는 크게 전개형 메시 안테나, 마이크로스트립 패치 안테나, 다이폴 안테나 등으로 구성된 배열 안테나가 탑재되는데 (Abulgasem et al. 2021, Liu et al. 2022), 패치 안테나의 구현 편의성과 구조적 안전성으로 인해 일반적으로 패치 안테나가 주로 활용된다 (Kim & Woo 2015). 배열 안테나를 이용하는 위성 시스템에서 지상의 불특정 신호를 관측하기 위해서는 탑재된 배열 안테나를 통해 수신된 신호의 도래각(Angle-of-Arrival, AOA) 정보가 필요하다. 추정된 도래각 정보를 바탕으로 원하는 방향으로 빔을 형성하여 임무를 수행하게 되는데, 위성 통신용 주파수가 상향됨에 따라 최근 저궤도 위성에도 고지향성의 예리한 빔 형상이 요구되고 있어 (Liu et al. 2022), 메시브 배열 안테나의 활용성이 커지고 있다. 위성에 대규모 배열 안테나를 탑재함으로써 고지향성의 예리한 빔을 형성할 수 있지만, 기존의 Multiple Signal Classification (MUSIC), Estimation of Signal Parameters via Rotational Invariant Techniques (ESPRIT) 등과 같은 고성능 신호 도래각 추정 알고리즘은 다수의 안테나 소자들을 사용함에 따라 그 복잡도가 급격히 상승하게 된다.
고성능 도래각 추정 알고리즘을 메시브 배열 안테나 형상에 효율적으로 적용하기 위한 Beamspace MUSIC (Zoltowski et al. 1993, Sun & Yang 2004), Beamspace ESPRIT (Xu et al. 1994, Liu et al. 2020) 등과 같은 기술들이 개발되었고, 복잡도 개선을 위한 도래각 추정 알고리즘이 연구되었다. Badawy et al. (2014)는 저복잡도 도래각 추정을 위해 선형 배열 안테나와 교차 상관관계를 이용하는 Cross-Correlation Switched Beam System (XSBS) 알고리즘을 제안하였다. Al-Sadoon et al. (2017)은 선형 및 원형 배열 안테나에 적용가능하고 센서 간 교차 상관 관계를 기반으로 하는 Propagator Direct Data Acquisition (PDDA) 기법을 제안하였다. Kim & Hwang (2020)은 메시브 정사각 배열 안테나를 기반으로 안테나 요소로 인한 도래각 추정 복잡도를 줄이기 위해 CAPON과 Beamspace MUSIC으로 구성된 캐스케이드 알고리즘을 제안하였다. Pan & Jiang (2020)은 메시브 선형 배열 안테나의 복잡도를 낮추는 BeamSpace Atomic Norm Minimization (BS-ANM) 기반 저복잡도 도래각 추정 알고리즘을 제안하였다. 하지만, 앞서 기술한 기존의 연구들은 일부 특정 배열 안테나(선형, 원형, 정사각) 형상이 적용된 도래각 추정에 관한 연구들이고, 최근 다양한 형상(L형상, Y형상, 사각형, 원형, 동심원, 컴포멀 구조 등)의 메시브 배열 안테나의 사용 빈도가 증가하고 있으나, 효율적으로 복잡도를 낮출 수 있는 빔공간 복잡도 분석 및 도래각 추정 알고리즘 적용에 대한 연구는 거의 이루어지지 않고 있다. 따라서, 본 논문은 메시브 배열 안테나를 활용하는 경우 효율적인 도래각 추정이 가능한 Kim & Hwang (2020)에서 제안된 캐스케이드 도래각 추정 알고리즘에 다양한 배열 안테나들의 형상을 적용하고, 도래각 추정을 위한 계산복잡도에 대한 수학적 모델을 제시하며, 컴퓨터 시뮬레이션을 통해 메시브 배열 안테나 형상 별 캐스케이드 도래각 추정 알고리즘의 복잡도를 분석한다.
본 논문의 구성은 다음과 같다. 2장에서 논문에서 고려된 메시브 배열 안테나 모델을 제시하고, 3장에서는 2장에서 제시된 배열 안테나 형상 기반의 캐스케이드 도래각 추정 알고리즘의 계산 복잡도 분석을 위한 수학적 모델을 제시한다. 4장에서는 3장의 수학적 모델을 기반으로 각 형상당 캐스케이드 도래각 추정 알고리즘의 계산복잡도를 비교하기 위한 컴퓨터 시뮬레이션 결과를 제공하고, 5장에서 본 논문의 결론을 맺는다.
본 장에서는 논문에서 고려하는 다섯 가지 형상의 대규모 배열 안테나 모델을 소개한다.
위성 시스템의 배열 안테나는 위성의 고도가 높아짐에 따라 개구 면적이 증가된 안테나를 사용하여야 하며, 높은 이득, 넓은 커버리지, 다중 빔형성, 빠른 빔조향 등 다양한 기능적 특성을 만족하여야 한다 (Wang et al. 2020). 메시브 배열 안테나는 이러한 조건을 충족시키는 배열 안테나로 (Zhang et al. 2015), 선형, 평면형(사각형, 원형, 동심원 등), 곡면형 등 다양한 형태로 제작이 가능하지만, 일반적으로 Fig. 1a의 정사각형 배열(Square Array, SA) 혹은 Fig. 1b의 직사각형 배열(Rectangular Array, RA)이 주로 사용되고 (Wang et al. 2020), 공간적인 제약사항 및 특정 목적이 있는 경우, Figs. 1c-e에 제시되어 있는 프레임 배열(Frame Array, FA), 원형 배열(Circular Array, CA), 동심원 배열(Concentric Circular Array, CCA) 안테나도 고려된다 (Bialkowski & Karmakar 1999, El-Hassan et al. 2019, Morris & Wong 2019).

Fig. 1. Massive array antenna configurations: (a) Square array (SA), (b) Rectangular array (RA), (c) Frame array (FA), (d) Circular array (CA), (e) Concentric circular array (CCA).
위성 시스템의 배열 안테나는 위성의 고도가 높아짐에 따라 개구 면적이 증가된 안테나를 사용하여야 하며, 높은 이득, 넓은 커버리지, 다중 빔형성, 빠른 빔조향 등 다양한 기능적 특성을 만족하여야 한다 (Wang et al. 2020). 메시브 배열 안테나는 이러한 조건을 충족시키는 배열 안테나로 (Zhang et al. 2015), 선형, 평면형(사각형, 원형, 동심원 등), 곡면형 등 다양한 형태로 제작이 가능하지만, 일반적으로 Fig. 1a의 정사각형 배열(Square Array, SA) 혹은 Fig. 1b의 직사각형 배열(Rectangular Array, RA)이 주로 사용되고 (Wang et al. 2020), 공간적인 제약사항 및 특정 목적이 있는 경우, Figs. 1c-e에 제시되어 있는 프레임 배열(Frame Array, FA), 원형 배열(Circular Array, CA), 동심원 배열(Concentric Circular Array, CCA) 안테나도 고려된다 (Bialkowski & Karmakar 1999, El-Hassan et al. 2019, Morris & Wong 2019).
본 장은 캐스케이드 도래각 추정 알고리즘을 간단히 소개하고, 다양한 메시브 배열 안테나 형상이 적용된 캐스케이드 알고리즘의 계산 복잡도 분석을 위한 수학적 모델을 제공한다. 캐스케이드 도래각 추정 알고리즘과 기존 알고리즘과의 복잡도 비교를 위해 다양한 배열 안테나에 적용이 가능한 Minimum Variance Distortionless Response (MVDR)과 MUSIC 같은 대표적인 도래각 추정 알고리즘을 고려한다.
MVDR알고리즘은 빔형성 알고리즘의 일종으로 Capon에 의해 제안되었으며 (Capon 1969), 안테나로 입사하는 신호의 출력 Signal to Noise Ratio (SNR)을 최대화하여 신호의 도래각을 추정하며, 배열 안테나에 사용되는 안테나 소자의 개수와 신호의 SNR에 의해 해상도가 좌우되지만, 고유값 분해가 요구되지 않아 빠른 도래각 추정이 가능하다 (Kiong et al. 2014). MUSIC 알고리즘은 Schmidt에 의해 처음 제안되었으며 (Schmidt 1986), 수신된 신호의 공분산행렬(Covariance matrix)의 고유치 분해를 통해 분석된 잡음 공분산 행렬을 활용하여 잡음 고유벡터에 직교하는 방향벡터 검색을 통해 신호의 도래각을 추정한다 (Park & Jeong 2006). 고유치 분해를 수행하기에 안테나 개수를 초과하는 신호의 도래각을 추정할 수 없고, 신호가 상관되어 있을 경우 성능의 열화가 발생하나, MVDR에 비해 고성능 도래각 추정 성능을 보유한다.
캐스케이드 도래각 추정 알고리즘은 유연한(Flexible) 메시브 배열 안테나를 기반으로 실시간 도래각 추정을 위해 Kim & Hwang (2020)에서 제안된 알고리즘이다. 기존의 부공간(Subspace) 기반 고분해능 알고리즘이 요소 공간에서 지니는 높은 복잡성 문제를 CAPON과 Beamspace MUSIC의 조합으로 해결한 알고리즘으로 동작 순서는 Fig. 2에 제시되어 있다. 먼저, 단시간에 다수의 신호 도래각들을 포함한 도래각 그룹을 대략적으로 추정하기 위해 메시브 배열 안테나의 전체 소자들 중 최소한의 소자들과 낮은 분해능을 적용한 CAPON을 수행한다. CAPON 알고리즘을 통해 도래각 그룹을 추정한 후, 추정된 그룹 내의 세부 신호 도래각들의 추정을 위해, 도래각 그룹의 중심각을 기반으로 빔공간 행렬이 적용된 Beamspace MUSIC을 수행한다. 정확한 상세 도래각 추정을 위해 메시브 배열 안테나의 전체 안테나 소자와 높은 분해능을 적용하지만 전체 범위가 아닌 추정된 도래각 그룹들에 한정된 범위만을 검색하며, 빔공간 행렬을 적용하여 요소 공간에 비해 상당히 축소된 차원의 신호를 기반으로 공분산 행렬을 계산하므로, 일반적인 도래각 추정 알고리즘에 비해 상당히 낮은 계산 복잡도가 가능하다.
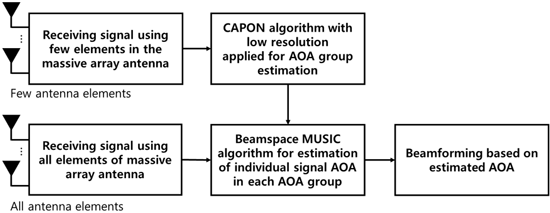
Fig. 2. Basic structure of cascade AOA estimation algorithm.
다음으로, 각 배열 안테나 형상에 기반한 캐스케이드 도래각 추정 알고리즘의 복잡도와 기존의 기술로 고려된 MVDR 및 MUSIC 알고리즘의 계산 복잡도를 분석하기 위한 수학적 모델을 제시한다.
CAPON 알고리즘은 공분산 행렬 및 역행렬 생성, 공간 스팩트럼 계산에 대한 덧셈/뺄셈, 곱셈/나눗셈에 대한 복잡도를 고려하며, Eqs. (1, 2)와 같이 정의된다 (Kim & Hwang 2020).
$$\text{CAPON}_{A/S} = \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 – 1 \right) + \frac{1}{3} M_c^3 + \left( T – \frac{1}{2} \right) M_c^2 – \frac{5}{6} M_c$$
$$\text{CAPON}_{M/D} = \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 + M_c \right) + \frac{1}{3} M_c^3 + \left( T + 1 \right) M_c^2 + \frac{2}{3} M_c$$
여기서 $\theta_{\text{range}}$, $\phi_{\text{range}}$, $M_c$, $\Delta_c$, $T$는 CAPON 알고리즘의 고도각(Elevation angle, $\theta$)과 방위각(Azimuth angle, $\theta$) 검색 범위, 사용한 안테나 개수, 분해능, 샘플링 횟수이며, 각각의 대규모 배열 안테나 형상을 적용하더라도 사용되는 개별 안테나 개수, 분해능, 샘플링 횟수가 동일하므로 일정한 상수 값으로 도출된다. 다만, 배열 형상에 따라 CAPON에서 사용하는 안테나 소자의 개수가 상이하고(Fig. 3), 추정되는 도래각 그룹의 검색 범위가 달라질 수 있으며, 신호가 넓게 퍼져있는 경우 다수개의 도래각 그룹 $(G_i, (i = 1, \ldots, F))$ 추정이 필요하다.
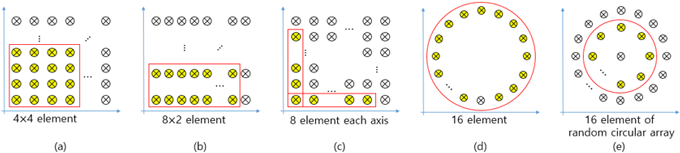
Fig. 3. Example of antenna element utilization in CAPON algorithm: (a) Square array (SA), (b) Rectangular array (RA), (c) Frame array (FA), (d) Circular array (CA), (e) Concentric circular array (CCA).
대략적으로 추정된 도래각 그룹에 대해, Beamspace MUSIC 알고리즘은 도래각 그룹 내 세부 도래각 추정을 위한 빔공간 공분산 행렬 생성, 공분산 행렬의 고유치 분해, 빔공간 조향 벡터 생성, 빔공간 잡음 부공간 행렬 계산, 공간스펙트럼 계산 등을 수행하여야 하는데, 이와 관련된 Beamspace MUSIC의 덧셈/뺄셈, 곱셈/나눗셈 복잡도는 Eqs. (3, 4)와 같다 (Kim & Hwang 2022).
$$B – \text{MUSIC}_{A/S} = \sum_{i=1}^{F} \left[ \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M – 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 – \left( T – L_i – \frac{1}{2} \right) B_{X-i}^2 – \left( T(M – 1) – \frac{1}{2} \right) B_{X-i} + 1 \right]$$
$$B – \text{MUSIC}_{M/D} = \sum_{i=1}^{F} \left[ \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M + 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 – \left( L_i + \frac{3}{2} \right) B_{X-i}^2 – \left( TM – \frac{19}{6} \right) B_{X-i} + 2 \right]$$
여기서 $\theta_{r-i}$ 및 $\phi_{r-i}$, $\Delta_{bm}$, $B_{X-i}$, $L_i$는 CAPON에 의해 추정된 i번째 도래각 그룹에 대한 Beamspace MUSIC의 검색 범위, 분해능, 배열 형태에 따른 빔공간 변환 행렬의 크기, 신호의 개수를 각각 의미한다.
다음으로, 메시브 배열 안테나 형상에 따른 빔공간 변환 복잡도를 고려한 캐스케이드 알고리즘의 총 복잡도에 대한 수학적 모델을 제시한다.
메시브 배열 안테나의 형상이 사각(정사각 혹은 직사각) 배열 안테나인 경우 Eq. (5)를 통해 빔공간 변환 행렬을 생성한다 (Kim & Hwang 2020).
$$B = \frac{1}{\sqrt{M_x N_y}} \mathbf{b}_y \otimes \mathbf{b}_x$$
여기서 $M_x$, $N_y$는 x축과 y축에 놓여있는 안테나 요소의 총 개수이고, $\mathbf{b}_x$, $\mathbf{b}_y$는 각 축에 대한 이산 푸리에 변환(Discrete Fourier Transform, DFT)을 의미하며, ⊗는 크로네커 곱(Kronecker product)을 나타낸다. 배열 형상이 사각 형상인 경우, 빔공간 변환 행렬 생성시 크로네커 곱을 활용하므로 덧셈/뺄셈 복잡도는 발생하지 않으며($\beta_{A/S}=0$), 곱셈/나눗셈 복잡도($\beta_{M/D}$)는 Eq. (6)과 같이 정의된다.
$$\beta_{M/D} = b_x b_y M_x N_y$$
여기서 $b_x \left( b_x \ll M_x \right)$와 $b_y \left( b_y \ll N_y \right)$는 각 좌표축의 DFT 행렬의 차수를 나타낸다. Eqs. (1-4)와 Eq. (6)을 고려한 사각 배열 안테나 기반의 캐스케이드 알고리즘의 총 덧셈/뺄셈 계산복잡도와 곱셈/나눗셈 복잡도는 Eqs. (7, 8)과 같이 주어진다.
$$\begin{align}
\text{Cascade – SA(RA) – Total}_{A/S} = & \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 – 1 \right) + \frac{1}{3} M_c^3 + \left( T – \frac{1}{2} \right) M_c^2 – \frac{5}{6} M_c \notag \\
& + \sum_{i=1}^{F} \left[ \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M – 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 – \left( T – L_i – \frac{1}{2} \right) B_{X-i}^2 \right. \notag \\
& \left. – \left( T(M – 1) – \frac{1}{2} \right) B_{X-i} + 1 \right]
\end{align}$$
$$\begin{align}
\text{Cascade – SA(RA) – Total}_{M/D} = & \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 + M_c \right) + \frac{1}{3} M_c^3 + \left( T + 1 \right) M_c^2 + \frac{2}{3} M_c + b_x b_y M_x N_y \notag \\
& + \sum_{i=1}^{F} \left[ \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M + 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 – \left( L_i + \frac{3}{2} \right) B_{X-i}^2 \right. \notag \\
& \left. – \left( TM – \frac{19}{6} \right) B_{X-i} + 2 \right]
\end{align}$$
평면 배열 안테나의 일종인 프레임 배열 안테나는 일반적인 사각 배열 안테나에서 중심부의 안테나 요소가 존재하지 않는 배열 안테나이다. 따라서, 빔공간 변환 행렬을 생성하기 위해 안테나를 $S_{x1} \times S_{y1}$, $S_{x2} \times S_{y2}$, $S_{x3} \times S_{y3}$, $S_{x4} \times S_{y4}$ 크기를 갖는 4개의 부배열로 나눈 후 Eqs. (9, 10)과 같이 크로네커 곱을 독립적으로 시행하여야 한다 (Kim & Hwang 2021).
$$B_{\text{sub1,sub3}} = \frac{1}{\sqrt{S_y (S_x – S_y)}} \mathbf{b}_y \otimes \mathbf{b}_x$$
$$B_{\text{sub2,sub4}} = \frac{1}{\sqrt{S_x (S_y – S_x)}} \mathbf{b}_x \otimes \mathbf{b}_y$$
여기서 $S_x$, $S_y$는 부 배열의 x축과 y에 놓인 안테나 요소의 총 개수를 의미한다. 프레임 배열도 사각 배열과 마찬가지로 빔공간 변환 행렬 생성시 크로네커 곱을 활용하기에 덧셈/뺄셈 복잡도는 발생하지 않으며($\beta_{FA-A/S} = 0$), 곱셈/나눗셈 복잡도($\beta_{FA-M/D}$)는 Eq. (11)과 같이 정의된다.
$$\beta_{FA-M/D} = (b_x b_y S_x S_y)_{\text{sub1}} + (b_x b_y S_x S_y)_{\text{sub1}} + (b_x b_y S_x S_y)_{\text{sub3}} + (b_x b_y S_x S_y)_{\text{sub4}}$$
Eqs. (1-4)와 Eq. (11)을 고려한 프레임 배열 안테나 기반의 캐스케이드 알고리즘의 총 덧셈/뺄셈 계산복잡도와 곱셈/나눗셈 복잡도는 Eqs. (12, 13)과 같이 주어진다.
$$\begin{align} \text{Cascade – FA – Total}_{A/S} = &\frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left(M_c^2 – 1\right) + \frac{1}{3} M_c^3 + \left(T – \frac{1}{2}\right) M_c^2 – \frac{5}{6} M_c \notag \\
&+ \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left(B_{X-i}^2 + (M – 1) B_{X-i}\right) + \frac{5}{3} B_{X-i}^3 \notag \\
&- \left(T – L_i – \frac{1}{2}\right) B_{X-i}^2 – \left(T(M – 1) – \frac{1}{2}\right) B_{X-i} + 1 \end{align}$$
$$\begin{align} \text{Cascade – FA – Total}_{M/D} = &\frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left(M_c^2 + M_c\right) + \frac{1}{3} M_c^3 + (T + 1) M_c^2 + \frac{2}{3} M_c \notag \\
&+ (b_x b_y S_x S_y)_{\text{sub1}} + (b_x b_y S_x S_y)_{\text{sub1}} + (b_x b_y S_x S_y)_{\text{sub3}} + (b_x b_y S_x S_y)_{\text{sub4}} \notag \\
&+ \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left(B_{X-i}^2 + (M + 1) B_{X-i}\right) + \frac{5}{3} B_{X-i}^3 – \left(L_i + \frac{3}{2}\right) B_{X-i}^2 \notag \\
&- \left(TM – \frac{19}{6}\right) B_{X-i} + 2 \end{align}$$
메시브 배열 안테나의 형상이 원형인 경우 빔공간 변환 행렬은 Eq. (14)를 통해 생성한다 (Belloni & Koivunen 2004).
$$\mathbf{B}_{CA} = \frac{1}{R} \mathbf{W}^H \mathbf{C} \mathbf{P}^H$$
여기서 $R$은 원형 배열 안테나 요소의 개수이고, $\mathbf{W}$는 가중치 행렬, $\mathbf{C}$는 빔공간 크기 조절을 위한 스케일 행렬, $\mathbf{P}$는 페이즈모드 행렬을 의미한다. 빔공간 변환 행렬 생성시 발생하는 덧셈/뺄셈, 곱셈/나눗셈 복잡도는 Eqs. (15, 16)과 같이 정의된다.
$$\beta_{CA-A/S} = (4P^2 + 2P)(2P + R)$$
$$\beta_{CA-M/D} = (2P + 1)^2 (2P + R + 1)$$
여기서 $P = k_0 r(2P < R)$는 원형 배열의 여기모드 최고차항이며, $P$의 $k_0$는 파상수(wavenumber), $r$은 원형 배열의 반지름을 의미한다. Eqs. (1-4)와 Eqs. (15, 16)을 고려한 원형 배열 안테나 기반의 캐스케이드 알고리즘의 총 덧셈/뺄셈 계산복잡도와 곱셈/나눗셈 복잡도는 Eqs. (17, 18)과 같이 주어진다.
$$\begin{align} \text{Cascade – CA – Total}_{A/S} = &\frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left(M_c^2 – 1\right) + \frac{1}{3} M_c^3 + \left(T – \frac{1}{2}\right) M_c^2 – \frac{5}{6} M_c \notag \\
&+ (4P^2 + 2P)(2P + R) \notag \\
&+ \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left(B_{X-i}^2 + (M – 1) B_{X-i}\right) + \frac{5}{3} B_{X-i}^3 \notag \\
&- \left(T – L_i – \frac{1}{2}\right) B_{X-i}^2 – \left(T(M – 1) – \frac{1}{2}\right) B_{X-i} + 1 \end{align}$$
$$\begin{align} \text{Cascade – CA – Total}_{M/D} = &\frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left(M_c^2 + M_c\right) + \frac{1}{3} M_c^3 + (T + 1) M_c^2 + \frac{2}{3} M_c \notag \\
&+ (2P + 1)^2 (2P + R + 1) \notag \\
&+ \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left(B_{X-i}^2 + (M + 1) B_{X-i}\right) + \frac{5}{3} B_{X-i}^3 – \left(L_i + \frac{3}{2}\right) B_{X-i}^2 \notag \\
&- \left(TM – \frac{19}{6}\right) B_{X-i} + 2 \end{align}$$
동심원 배열 안테나는 중심을 공유하는 반경이 서로 다른 $K$개의 원형 배열 안테나가 결합된 형태이다. 원형 배열 안테나의 반경에 따라, 각 원형 배열에 대한 빔공간 변환 행렬을 정의하여야 하며, $k$번째 원형 배열에 대한 빔공간 변환 행렬은 Eq. (19)와 같이 정의된다 (Ma et al. 2018).
$$\mathbf{B}_{CA-k} = \frac{1}{R_k} \mathbf{W}_k^H \mathbf{C}_k \mathbf{P}_k^H$$
여기서 $R_k$, $\mathbf{W}_k$, $\mathbf{C}_k$, $\mathbf{P}_k$는 각각 $k$번째 원형 배열 안테나에 놓인 안테나 요소의 총 개수, 가중치 행렬, 스케일 행렬, 페이즈 모드 행렬을 의미한다. 동심원 배열 안테나의 전체 배열을 고려한 빔공간 변환 행렬 생성시 발생하는 덧셈/뺄셈, 곱셈/나눗셈 복잡도는 Eqs. (20, 21)과 같이 정의된다.
$$\beta_{CCA-A/S} = \sum_{k=1}^{K} (4P_k^2 + 2P_k)(2P_k + R_k)$$
$$\beta_{CCA-M/D} = \sum_{k=1}^{K} (2P_k + 1)^2 (2P_k + R_k + 1)$$
여기서 $P_k = k_0 r_k (2P_k < R_k)$는 동심원 배열 안테나의 $k$번째 원형 배열에 대한 여기모드 최고차항을 나타내고, $P_k$의 $r_k$는 $k$번째 원형 배열의 반지름이다. Eqs. (1-4)와 Eqs. (20, 21)을 고려한 동심원 배열 안테나 기반의 캐스케이드 알고리즘의 총 덧셈/뺄셈 계산복잡도와 곱셈/나눗셈 복잡도는 Eqs. (22, 23)과 같이 정리할 수 있다.
$$\begin{align}
\text{Cascade – CCA – Total}_{A/S} =\
& \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 – 1 \right) + \frac{1}{3} M_c^3 + \left( T – \frac{1}{2} \right) M_c^2 – \frac{5}{6} M_c \notag \\
& + \sum_{k=1}^{K} (4P_k^2 + 2P_k)(2P_k + R_k) \notag \\
& + \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M – 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 \notag \\
& – \left( T – L_i – \frac{1}{2} \right) B_{X-i}^2 – \left( T(M – 1) – \frac{1}{2} \right) B_{X-i} + 1
\end{align}$$
$$\begin{align}
\text{Cascade – CCA – Total}_{M/D} =\
& \frac{\theta_{\text{range}} \phi_{\text{range}}}{\Delta_c^2} \left( M_c^2 + M_c \right) + \frac{1}{3} M_c^3 + \left( T + 1 \right) M_c^2 + \frac{2}{3} M_c \notag \\
& + \sum_{k=1}^{K} (2P_k + 1)^2 (2P_k + R_k + 1) \notag \\
& + \sum_{i=1}^{F} \frac{\theta_{r-i} \phi_{r-i}}{\Delta_{bm}^2} \left( B_{X-i}^2 + (M + 1) B_{X-i} \right) + \frac{5}{3} B_{X-i}^3 \notag \\
& – \left( L_i + \frac{3}{2} \right) B_{X-i}^2 – \left( TM – \frac{19}{6} \right) B_{X-i} + 2
\end{align}$$
캐스케이드 도래각 추정 알고리즘과 일반적인 도래각 추정 알고리즘의 복잡도 비교를 위해, MVDR과 MUSIC 알고리즘의 계산 복잡도에 대한 수학적 모델을 제시한다.
MVDR 알고리즘은 도래각 추정 시 캐스케이드 CAPON 알고리즘과 동일한 매개변수를 고려하지만, 전체 안테나 요소를 사용하여야 한다. 따라서, MVDR 알고리즘의 덧셈/뺄셈, 곱셈/나눗셈 계산 복잡도는 Eqs. (24, 25)와 같이 주어진다.
$$\text{MVDR}_{A/S} = \frac{\theta_{range} \phi_{range}}{\Delta_{MVDR}^2} \left( M^2 – 1 \right) + \frac{1}{3} M^3 + \left( T – \frac{1}{2} \right) M^2 – \frac{5}{6} M$$
$$\text{MVDR}_{M/D} = \frac{\theta_{range} \phi_{range}}{\Delta_{MVDR}^2} \left( M^2 + M \right) + \frac{1}{3} M^3 + \left( T + 1 \right) M^2 + \frac{2}{3} M$$
여기서 $\Delta_{MVDR}$은 MVDR 알고리즘의 분해능이다.
MUSIC 알고리즘은 도래각 추정 시 요소 공간에서 모델링된 공분산 행렬 생성, 공분산 행렬의 고유치 분해, 잡음 부공간 행렬 계산, 공간 스펙트럼 계산을 수행하여야 하는데, 이에 대한 MUSIC 알고리즘의 덧셈/뺄셈, 곱셈/나눗셈 복잡도는 Eqs. (26, 27)과 같이 주어진다.
$$\text{MUSIC}_{A/S} = \frac{\theta_{range} \phi_{range}}{\Delta_{MUSIC}^2} \left( M^2 – 1 \right) + \frac{5}{3} M^3 + \left( T – L + \frac{3}{2} \right) M^2 – \frac{1}{2} M + 1$$
$$\text{MUSIC}_{M/D} = \frac{\theta_{range} \phi_{range}}{\Delta_{MUSIC}^2} \left( M^2 + M \right) + \frac{5}{3} M^3 + \left( T – L – \frac{1}{2} \right) M^2 + \frac{19}{6} M + 2$$
여기서 $\Delta_{MUSIC}$은 MUSIC 알고리즘의 분해능이고, $L$은 수신신호에 포함된 신호의 총 개수를 의미한다.
본 장은 다양한 대규모 배열 안테나 형상에 대한 캐스케이드 도래각 추정 알고리즘의 계산 복잡도 분석을 위한 시뮬레이션 결과를 제시한다. 또한, 캐스케이드 알고리즘의 계산 복잡도를 MVDR 및 MUSIC과 같은 일반적인 도래각 추정 알고리즘의 계산 복잡도와 비교한 결과를 제시한다.
시뮬레이션을 위해 Fig. 4에 제시되어 있는 안테나 형상 및 구조를 고려하였으며, 안테나의 개수는 256개, 프레임 배열과 동심원 배열은 2개의 배열로 구성된다고 가정한다. 대규모 배열 안테나 형상 별 빔공간 복잡도를 분석하기 위해 빔공간 변환 행렬의 크기를 증가시켜 가며 시뮬레이션을 진행하였는데, 빔공간 변환 행렬의 크기는 수식적으로 동일한 크기를 생성할 수 없어 최대한 유사한 값을 비교하기 위해 정사각 배열, 직사각배열, 원형 배열은 9, 27, 45, 81을 고려하였고, 프레임 배열과 동심원 배열은 8, 28, 44, 80을 고려하였다.

Fig. 4. Massive array antenna configurations for computer simulation.
Fig. 5는 안테나 형상 별 빔공간 변환 행렬 생성 복잡도에 대한 시뮬레이션 결과로 사각 형상(정사각, 직사각, 프레임)의 배열 안테나가 원형 형상(원형, 동심원)의 배열 안테나에 비해 복잡도가 낮은 경향을 보인다. 정사각 배열, 직사각배열, 원형 배열의 빔공간 행렬의 크기가 9에서 81로, 프레임 배열과 동심원 배열의 빔공간 행렬의 크기가 8에서 80으로 각각 9배와 10배 증가할 때 사각 형상(정사각, 직사각, 프레임) 배열 안테나는 덧셈/뺄셈 복잡도는 발생하지 않으며, 곱셈/나눗셈 복잡도는 각각 9배, 9배, 10배 증가하였다. 반면 원형 형상(원형, 동심원) 배열 안테나의 덧셈/뺄셈 복잡도는 각각 257배, 159배 증가하였으며, 곱셈/나눗셈 복잡도는 222배, 124배 증가하였다. 이는 사각 형상(정사각, 직사각, 프레임) 배열 안테나의 경우 크로네커 곱의 특성에 기인하며, 원형 형상(원형, 동심원) 배열 안테나의 경우 빔공간 변환 행렬을 생성하기 위해 서로 다른 3개의 행렬에 대한 곱이 수행되어야 하는데, 빔공간 변환 행렬의 크기가 증가할수록 각 행렬의 크기가 증가하여 발생하는 복잡도에 기인한다. 따라서, 원형 및 동심원 배열을 사용하는 시스템에서는 빔공간 행렬의 크기에 따라 계산 복잡도가 크게 증가할 수 있으므로, 최적화를 통해 적절히 복잡도를 감소시킬 필요성이 있다.
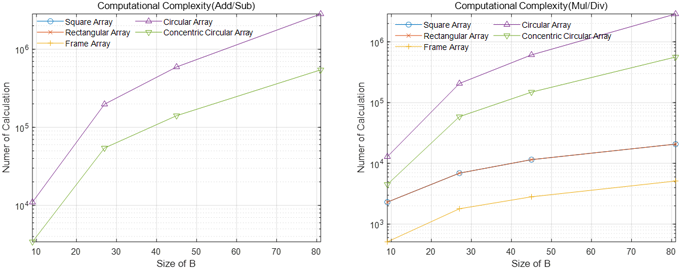
Fig. 5. Results of the beamspace transformation computational complexity analysis for each massive array antenna configurations.
논문에서 제시한 메시브 배열 안테나를 적용한 캐스케이드, MVDR, MUSIC 알고리즘의 총 계산 복잡도 비교와 도래각 추정 프로세스 타임 비교를 위해 20 dB의 SNR을 갖는 3개의 신호가 (20°, 25°, 30°)의 고도각과 (20°, 25°, 30°) 방위각으로 입사하여 하나의 도래각 그룹을 형성하는 시나리오를 가정하였다. 평면 배열 안테나는 고도각과 방위각 추정 시 -180°~180° 범위에 대해 추정이 가능하지만, 시뮬레이션 용이성을 위해 검색 범위를 0°~180°까지의 범위로 제한하였으며, 시뮬레이션 매개변수는 Table 1에 요약되어 있다.
Table 1. Simulation parameters.
| Massive array antenna configuration | ||||||
|---|---|---|---|---|---|---|
| SA | RA | FA | CA | CCA | ||
| Resolution | Δc | 5° | ||||
| Δbm | 0.1° | |||||
| ΔMVDR | 0.1° | |||||
| ΔMUSIC | 0.1° | |||||
| Number of antenna | Mc | 4×4 | 8×2 | Sub1,3 : 4×1 Sub2,4 : 1×4 | 16 element | 16 element of inner circular array |
| M | 16×16 | 32×8 | Sub1,3 : 32×2 Sub2,4 : 2×32 | 256 element | Inner: 128 element Outer: 128 element | |
| Search range | θrange | 180° | ||||
| φrange | 180° | |||||
| θr-i | According to spatial spectral analysis of the CAPON algorithm | |||||
| φr-i | According to spatial spectral analysis of the CAPON algorithm | |||||
| Sampling number | T | 10240 | ||||
| Number of signal | L | 3 | ||||
| Li | 3 | |||||
| Size of B | Bx-i | 36 | 40 | 40 | 39 | 40 |
Table 1의 매개변수가 적용된 캐스케이드 알고리즘의 CAPON 공간 스펙트럼 분석결과는 Fig. 6에 제시되어 있으며, Fig. 7은 도래각 그룹 결정을 위해 10 dB의 임계값을 적용한 공간스펙트럼의 단면도이다. 배열 형상에 따른 도래각 그룹의 범위는 SA, RA는 고도각 10°~40°, 방위각 0°~40°, FA, CA, CCA는 고도각 15°~35°, 방위각 15°~35°로 추정되었다. Fig. 8은 모든 안테나 소자와 0.1° 분해능을 적용한 캐스케이드 알고리즘의 Bemaspace MUSIC 알고리즘 (Fig. 8 좌측), MVDR 알고리즘 (Fig. 8 중앙), MUSIC 알고리즘 (Fig. 8 우측)의 공간스펙트럼으로, 메시브 배열 안테나 적용으로 20°, 25°, 30°의 고도각과 20°, 25°, 30°의 방위각으로 입사하는 신호의 도래각을 정확히 추정함을 확인할 수 있다.
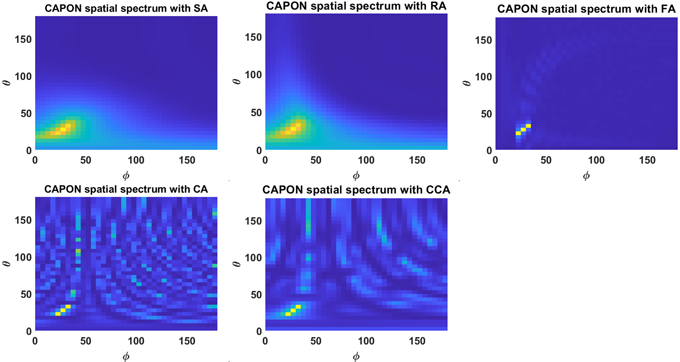
Fig. 6. CAPON spatial spectrum for AOA group estimation for each massive array antenna configuration.
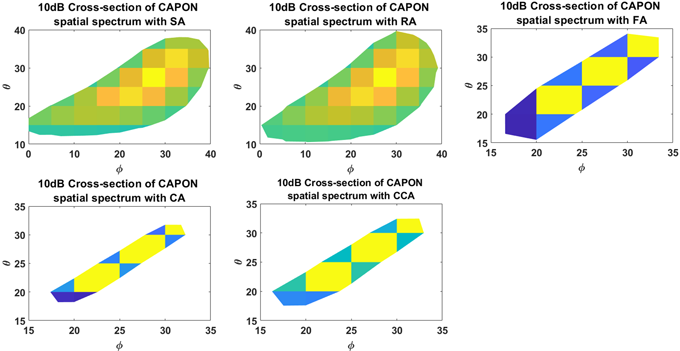
Fig. 7. CAPON spatial spectrum cross-section with 10 dB threshold for AOA group estimation.
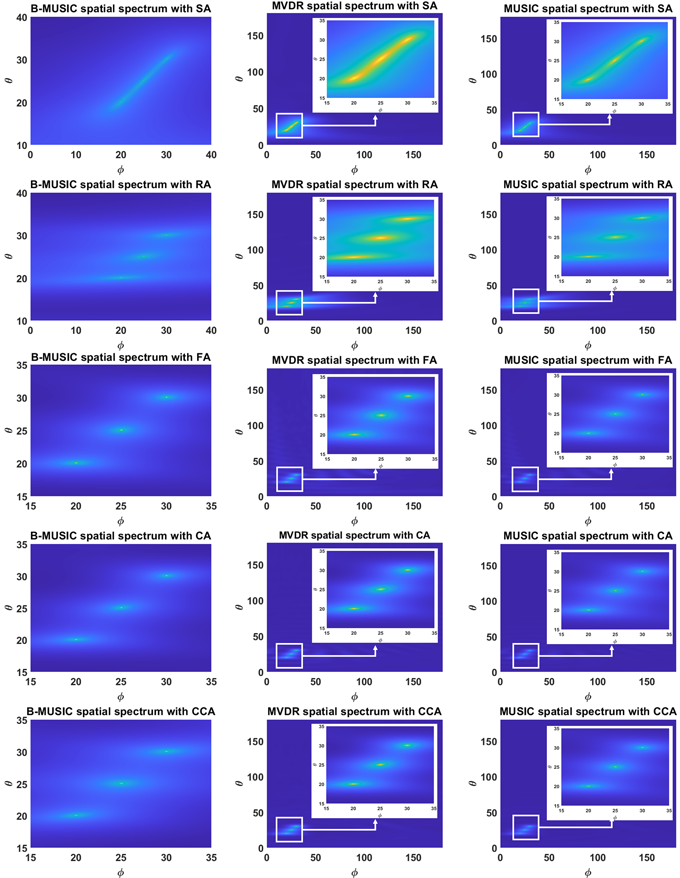
Fig. 8. Individual AOA estimation results for each algorithm applying each massive array antenna configuration: left; cascade (beamspace MUSIC), center; MVDR, right; MUSIC.
Fig. 9는 고려된 알고리즘들의 도래각 추정 처리시간(processing time)을 나타낸 것인데, 캐스케이드 알고리즘은 약 2.5초, MVDR 알고리즘은 평균적으로 약 164초, MUSIC 알고리즘은 평균적으로 약 266초로 캐스케이드 도래각 추정 알고리즘이 MVDR과 MUSIC에 비해 각각 98%와 99% 감소된 현저히 낮은 처리시간이 필요하다는 것을 확인할 수 있다. Table 1의 매개변수들을 고려한 5가지 형상의 대규모 배열 안테나가 적용된 각 알고리즘의 총 복잡도 분석 결과는 Fig. 10에 제시되어 있다. 그림으로부터 고려된 모든 안테나 형상에 대하여, 캐스케이드 도래각 추정 알고리즘이 MVDR과 MUSIC 대비 약 99% 낮은 총 복잡도를 보유함을 확인할 수 있다.
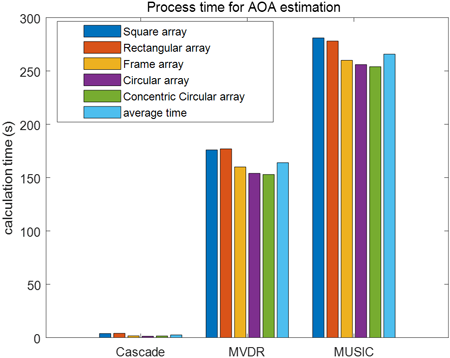
Fig. 9. Comparison of AOA estimation process times for each massive array antenna configuration.
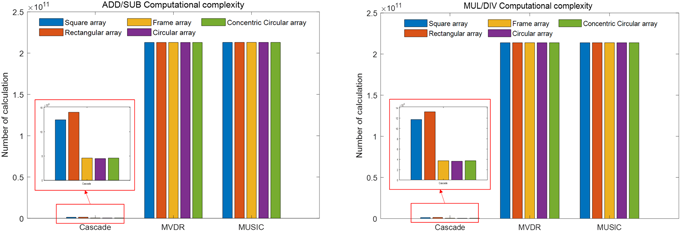
Fig. 10. Analysis of total computational complexity of addition/subtraction, multiplication/division of cascade, MVDR, and MUSIC applied to each massive array antenna configuration.
최근 통신, 지구 관찰 등의 목적으로, 위성을 활용한 다양한 연구가 활발히 진행되고 있으며, 위성 통신 주파수 향상으로 고지향성의 예리한 빔 형상이 요구됨에 따라 메시브 배열 안테나의 활용성이 증대되고 있다. 메시브 배열 안테나를 기반으로 신호의 도래각을 추정하는 경우, 기존 알고리즘의 높은 복잡도로 인해 실시간 추정을 보장하기 어렵다. 이러한 문제를 개선하기 위해 최근 캐스케이드 도래각 추정 알고리즘이 제안되었다. 본 논문은 다양한 형태의 메시브 배열 안테나 형상을 캐스케이드 도래각 추정 알고리즘에 적용하여 복잡도를 비교하고 그 결과를 분석하였다. 이를 위해, 다섯 가지 형상의 메시브 배열 안테나를 제시하고 형상 별 계산 복잡도 분석을 위한 수학적 모델을 제시하였으며, 캐스케이드 도래각 추정 알고리즘과 일반적인 도래각 추정 알고리즘의 복잡도 비교를 위해 MVDR과 MUSIC을 선택하여 비교 분석하였다. 복잡도 및 처리시간에 대한 시뮬레이션 결과, 모든 안테나 형상에 대해 캐스케이드 도래각 추정 알고리즘이 MVDR 및 MUSIC에 비해 현저히 낮은 결과를 보임일 확인할 수 있다. 즉, 캐스케이드 도래각 추정 알고리즘이 일반적인 도래각 추정 알고리즘과 유사한 추정 성능을 가지면서 현저히 낮은 복잡도 및 처리시간을 가지고 있어, 보다 효율적인 기술이라고 판단된다.
이 논문은 2024년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임 (NRF-2022R1A6A3A01087346).
Conceptualization, T. Kim. and S. Hwang; methodology, T. Kim. and S. Hwang; validation, T. Kim; formal analysis, T. Kim; investigation, T. Kim. and S. Hwang; writing—original draft preparation, T. Kim. writing—review and editing, S. Hwang; supervision; S. Hwang.
The authors declare no conflict of interest.
Abulgasem, S., Tubbal, F., Raad, R., Theoharis, P. I., Lu, S., et al. 2021, Antenna designs for CubeSats: A review, IEEE Access, 9, 45289-45324. https://doi.org/10.1109/ACCESS.2021.3066632
Al-Sadoon, M. A. G., Ali, N. T., Dama, Y., Zuid, A., Jones, S. M. R., et al. 2017, A new low complexity angle of arrival algorithm for 1D and 2D direction estimation in MIMO smart antenna systems, Sensors, 17, 1-19. https://doi.org/10.3390/s17112631
Badawy, A., Khattab, T., Trinchero, D., Fouly, T. E., & Mohamed, A. 2014, A simple AoA estimation scheme, arXiv preprint arXiv:1409.5744, 1-7. https://doi.org/10.48550/arXiv.1409.5744
Belloni, F. & Koivunen, V. 2004, Analysis of beamspace transform on uniform circular array, In Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7-10 Nov. 2004, pp.1963-1967. https://doi.org/10.1109/ACSSC.2004.1399507
Bialkowski, M. E. & Karmakar, N. C. 1999, A two-ring circular phased-array antenna for mobile satellite communications, IEEE Antennas and propagation Magazine, 41, 14-23. https://doi.org/10.1109/74.775244
Capon, J. 1969, High resolution frequency-wavenumber spectrum analysis, Proceedings of the IEEE, 57, 1408-1418, https://doi.org/10.1109/PROC.1969.7278
El-Hassan, M. A., Awadalla, K. H., & Hussein, K. F. A. 2019, Shaped beam circularly polarized circular array for SAR and satellite applications, in 2019 36th National Radio Science Conference (NRSC), Port Said, Egypt, 16-18 April 2019, pp.11-21. https://doi.org/10.1109/NRSC.2019.8734663
Kim, J.-W. & Woo, J.-M. 2015, A Design of Isoflux Radiation Pattern Microstrip Patch Antenna for LEO Medium-sized Satellites, The Journal of The Korea Institute of Intelligent Transport Systems, 14, 24-29. https://doi.org/10.12815/kits.2015.14.2.024
Kim, T. & Hwang, S. 2020, Cascade AOA estimation algorithm based on flexible massive antenna array, Sensors, 20, 1-23. https://doi.org/10.3390/s20236797
Kim, T. & Hwang, S. 2021, Angle-of-Arrival Estimation Algorithm Based on Combined Array Antenna, JPNT, 10, 131-137. https://doi.org/10.11003/JPNT.2021.10.2.131
Kim, T. & Hwang, S. 2022, Computational Complexity Analysis of Cascade AOA Estimation Algorithm Based on FMCCA Antenna, JPNT, 11, 91-98. https://doi.org/10.11003/JPNT.2022.11.2.91
Kiong, T. S., Salem, S. B., Paw, J. K. S., Sankar, K. P., & Darzi, S. 2014, Minimum variance distortionless response beamformer with enhanced nulling level control via dynamic mutated artificial immune system, The Scientific World J., 2014, 1-9. https://doi.org/10.1155/2014/164053
Liu, S., Theoharis, P. I., Raad, R., Tubbal, F., Theoharis, A., et al. 2022, A survey on CubeSat missions and their antenna designs, Electronics, 11, 1-39. https://doi.org/10.3390/electronics11132021
Liu, Y., Hou, L., Shen, Q., Lv, C., Na, S., et al. 2020, Beamspace U-ESPRIT DOA estimation algorithm of coherently distributed sources in massive MIMO systems, In 2020 12th International Conference on Advanced Computational Intelligence (ICACI), Dali, China, 14-16 Aug. 2020, pp.126-132. https://doi.org/10.1109/ICACI49185.2020.9177726
Ma, Y., Wang, X., & Cao, X. 2018, Coarray beamspace transformation based DOA estimation for uniform circular arrays, In 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23-27 April 2018, pp.792-797. https://doi.org/10.1109/RADAR.2018.8378661
Morris, Z. N. & Wong, K. T. 2019, Comparing the “Rim” Versus the “Filled” Rectangular Array Grids—Their Direction-Finding Cramér-Rao Bounds, IEEE Transactions on Aerospace and Electronic Systems, 55, 1945-1956. https://doi.org/10.1109/TAES.2018.2879555
Pan, J. & Jiang, F. 2020, Low complexity beamspace super resolution for DOA estimation of linear array, Sensors, 20, 1-19. https://doi.org/10.3390/s20082222
Park, B. W. & Jeong, B. S. 2006, Design of MUSIC algorithm for DOA estimation, Journal of the Institute of Convergence Signal Processing, 7, 189-194.
Schmidt, R. 1986, Multiple emitter location and signal parameter estimation, IEEE transactions on antennas and propagation, 34, 276-280. https://doi.org/10.1109/TAP.1986.1143830
Sun, C. & Yang, Y.-x. 2004, On beampattern design for beamspace music, Acoustical science and technology, 25, 2-8. https://doi.org/10.1250/ast.25.2
Wang, C., Wang, Y., Lian, P., Xue, S., Xu, Q., et al. 2020, Space phased array antenna developments: A perspective on structural design, IEEE Aerospace and Electronic Systems Magazine, 35, 44-63. https://doi.org/10.1109/MAES.2020.2984300
Xu, G., Silverstein, S. D., Roy, R. H., & Kailath, T. 1994, Beamspace esprit, IEEE Transactions on Signal Processing, 42, 349-356. https://doi.org/10.1109/78.275607
Zhang, J. A., Huang, X., Dyadyuk, V., & Guo, Y. J. 2015, Massive hybrid antenna array for millimeter-wave cellular communications, IEEE Wireless Communications, 22, 79-87. https://doi.org/10.1109/MWC.2015.7054722
Zoltowski, M. D., Kautz, G. M., & Silverstein, S. D. 1993, Beamspace root-MUSIC, IEEE Transactions on Signal Processing, 41, 344-364. https://doi.org/10.1109/TSP.1993.193151